单选址问题

比较了1）迭代法，2）重心法和3）one-median法的差异。总体而言从加权距离最小的角度看，迭代法选出来的结果最好。当网点和网点的单量呈现偏态分布时，one-median的结果更好，当网点和网点的单量呈现呈现随机分布时，重心法和one-median没有明显的差异。
参考链接：https://wiki.mbalib.com/zh-tw/%E9%87%8D%E5%BF%83%E6%B3%95

代码

  1. import numpy as np
  2. import pandas as pd
  3. import random
  4. import math as m
  5. import matplotlib
  6. import matplotlib.pyplot as plt
  7. import matplotlib.font_manager as fm
  8. plt.rcParams['font.sans-serif'] = [u'SimHei']
  10. """
  11. 单选址问题
  12. 比较了1）迭代法，2）重心法和3）one-median法的差异。总体而言从加权距离最小的角度看，迭代法选出来的结果最好。当网点和网点的单量呈现偏态分布时，one-median的结果更好，当网点和网点的单量呈现呈现随机分布时，重心法和one-median没有明显的差异。
  13. 参考链接：https://wiki.mbalib.com/zh-tw/%E9%87%8D%E5%BF%83%E6%B3%95
  14. """
  16. class Weight:
  17.     def __init__(self):
  18.         pass
  20.     def generate_data_handle(self):
  22.         # 生成数据
  23.         x_list = [6, 4, 1, 9, 3]
  24.         y_list = [7, 2, 6, 3, 10]
  25.         w_list = [8000, 7000, 5000, 4000, 6000]
  26.         cost_list = [1, 1, 1, 1, 1]
  27.         data = pd.DataFrame({'x': x_list, 'y':y_list, 'w': w_list, 'cost': cost_list})
  28.         data['w'] = data['w'] * data['cost']
  29.         data['w^2'] = data['w'] * data['w']
  30.         self.data = data
  32.     def generate_data_random(self, batch_size=20, p_lb=0, p_ub=100):
  34.         # 生成数据
  35.         y_list = [random.randint(60, 110) for i in range(batch_size)]
  36.         x_list = [random.randint(20, 50) for i in range(batch_size)]
  37.         w_list = [random.randint(10, 100)*x_list[i] for i in range(batch_size)]
  38.         cost_list = [1 for i in range(batch_size)]
  39.         data = pd.DataFrame({'x': x_list, 'y': y_list, 'w': w_list, 'cost': cost_list})
  40.         data['w'] = data['w'] * data['cost']
  41.         data['w^2'] = data['w'] * data['w']
  42.         self.data = data
  44.     def generate_data_skewness(self, batch_size=20, p_lb=0, p_ub=100):
  46.         # 生成数据
  47.         y_list = [random.randint(60, 110) for i in range(2*batch_size)]
  48.         y_list.extend([random.randint(80, 110) for i in range(2*batch_size)])
  49.         x_list = [random.randint(20, 50) for i in range(2*batch_size)]
  50.         x_list.extend([random.randint(40, 50) for i in range(2*batch_size)])
  51.         w_list = [random.randint(10, 100)*x_list[i] for i in range(4*batch_size)]
  52.         cost_list = [1 for i in range(4*batch_size)]
  53.         data = pd.DataFrame({'x': x_list, 'y': y_list, 'w': w_list, 'cost': cost_list})
  54.         data['w'] = data['w'] * data['cost']
  55.         data['w^2'] = data['w'] * data['w']
  56.         self.data = data
  58.     def compute_node_weight(self, data, weight_col_name, d_j):
  60.         # 普通重心法：加权均值：(x0, y0)
  61.         WC = np.array(data[weight_col_name])
  62.         WC_j = WC / d_j
  63.         WCX = ((np.array(data['x']) * WC)/d_j).sum()
  64.         WCY = ((np.array(data['y']) * WC)/d_j).sum()
  65.         x = WCX / WC_j.sum()
  66.         y = WCY / WC_j.sum()
  67.         d_j = ((np.array(data['x']) - x) ** 2 + (np.array(data['y']) - y) ** 2) ** 0.5
  68.         transportation_cost = (np.array(data['w']) * d_j).sum()
  69.         return x, y, d_j, transportation_cost
  71.     def run(self, iter_num=10):
  73.         # one - median法: 加权平方均值
  74.         x2, y2, d_j, transportation_cost2 = self.compute_node_weight(self.data, 'w^2', 1)
  75.         print('加权平方重心选点大致位置：({}，{}), 总运输费用：{}'.format(x2, y2, transportation_cost2))
  76.         # 加权均值
  77.         x0, y0, d_j, transportation_cost0 = self.compute_node_weight(self.data, 'w', 1)
  78.         print('重心法选点大致位置：({}，{}), 总运输费用：{}'.format(x0, y0, transportation_cost0))
  80.         self.p0 = [x0, y0, transportation_cost0]
  81.         self.p2 = [x2, y2, transportation_cost2]
  82.         min_transportation_cost = transportation_cost0
  83.         result_list = [[x0, y0, transportation_cost0, 0]]
  84.         for i in range(iter_num):
  85.             x, y, d_j, transportation_cost = self.compute_node_weight(self.data, 'w', d_j)
  86.             result_list.append([x, y, transportation_cost, i+1])
  87.             print('经{}次迭代后选址点位置：({},{}), 总运输费用：{}'.format(i + 1, x, y, transportation_cost))
  89.             if min_transportation_cost - transportation_cost < 1:
  90.                 break
  91.             min_transportation_cost = transportation_cost
  93.         self.result = result_list
  95.     def plot_figure(self):
  96.         # 初始化函数用于绘制一块干净的画布，为后续绘图做准备
  97.         result = self.result
  98.         p0, p2 = self.p0, self.p2
  100.         scatter_size = 200 # [200, 200, 200, 200, 200, 200]
  102.         # 生成画布
  103.         # plt.figure(figsize=(6, 6), dpi=80)
  104.         plt.subplot(1, 2, 1)
  105.         # 打开交互模式
  106.         plt.ion()
  107.         for step in range(len(result)):
  108.             # 清除原有图像
  109.             plt.cla()
  110.             position = result[step]
  111.             plt.scatter(self.data['x'], self.data['y'], scatter_size, c='pink', marker='*', alpha=0.7, label='配送点')
  112.             plt.scatter(p0[0], p0[1], scatter_size, c='blue', marker='p', alpha=0.7, label='加权重心')
  113.             plt.scatter(p2[0], p2[1], scatter_size, c='green', marker='p', alpha=0.7, label='加权平方重心')
  114.             plt.scatter(position[0], position[1], scatter_size, c='red', marker='p', alpha=0.7, label='选址点')
  115.             plt.xlabel('纬度', fontsize=11)
  116.             plt.ylabel('经度', fontsize=11)
  117.             plt.grid(True)
  118.             #     plt.text(1，3,'总费用{}'.format(T),fontsize=16)
  119.             plt.title('重心法选址,第{}次结果示意图'.format(step + 1), fontsize=14)
  120.             # plt.title('重心法选址结果示意图', fontsize=14)
  121.             plt.legend(loc='lower left')
  122.             plt.pause(0.2)
  124.         # 关闭交互模式
  125.         plt.ioff()
  126.         # 图形显示
  127.         # plt.show()
  129.     def plot_iteration(self):
  130.         result = self.result
  131.         p0, p2 = self.p0, self.p2
  132.         iter_num = len(result)
  133.         # 生成画布
  134.         # plt.figure(figsize=(6, 6), dpi=80)
  135.         plt.subplot(1, 2, 2)
  136.         plt.plot([0, iter_num-1], [p0[2], p0[2]], c='blue', label='加权重心')
  137.         plt.plot([0, iter_num-1], [p2[2], p2[2]], c='green', label='加权平方重心')
  138.         plt.plot([i for i in range(iter_num)], [p[2] for p in result], c='red', label='重心法')
  140.         plt.xlabel('迭代次数', fontsize=11)
  141.         plt.ylabel('总运输成本', fontsize=11)
  143.         plt.grid(True)
  144.         plt.title('重心法选址结果示意图', fontsize=14)
  145.         plt.legend(loc='lower left')
  146.         plt.show()
  149.     def plot_figure_subplot(self):
  150.         # 初始化函数用于绘制一块干净的画布，为后续绘图做准备
  151.         result = self.result
  152.         p0, p2 = self.p0, self.p2
  153.         scatter_size = 200 # [200, 200, 200, 200, 200, 200]
  154.         iter_num = len(result)
  156.         # 生成画布
  157.         plt.figure(figsize=(10, 6), dpi=80)
  158.         plt.subplot(1, 2, 1)
  159.         # 打开交互模式
  160.         plt.ion()
  161.         for step in range(len(result)):
  162.             # 清除原有图像
  163.             plt.cla()
  164.             position = result[step]
  165.             plt.scatter(self.data['x'], self.data['y'], scatter_size, c='pink', marker='*', alpha=0.7, label='配送点')
  166.             plt.scatter(p0[0], p0[1], scatter_size, c='blue', marker='p', alpha=0.7, label='重心法')
  167.             plt.scatter(p2[0], p2[1], scatter_size, c='green', marker='p', alpha=0.7, label='one-median')
  168.             plt.scatter(position[0], position[1], scatter_size, c='red', marker='p', alpha=0.7, label='迭代法选址点')
  169.             plt.xlabel('纬度', fontsize=11)
  170.             plt.ylabel('经度', fontsize=11)
  171.             plt.grid(True)
  172.             #     plt.text(1，3,'总费用{}'.format(T),fontsize=16)
  173.             plt.title('重心法选址,第{}次结果示意图'.format(step + 1), fontsize=14)
  174.             # plt.title('重心法选址结果示意图', fontsize=14)
  175.             plt.legend(loc='lower left')
  176.             plt.pause(0.2)
  178.         # 关闭交互模式
  179.         plt.ioff()
  181.         plt.subplot(1, 2, 2)
  182.         plt.plot([0, iter_num-1], [p0[2], p0[2]], c='blue', label='重心法')
  183.         plt.plot([0, iter_num-1], [p2[2], p2[2]], c='green', label='one-median')
  184.         plt.plot([i for i in range(iter_num)], [p[2] for p in result], c='red', label='迭代法选址点')
  186.         plt.xlabel('迭代次数', fontsize=11)
  187.         plt.ylabel('总运输成本', fontsize=11)
  189.         plt.grid(True)
  190.         plt.title('重心法选址结果示意图', fontsize=14)
  191.         plt.legend(loc='lower left')
  192.         plt.show()
  194. if __name__ == "__main__":
  195.     weight_compare = Weight()
  196.     # 生成小测试算例
  197.     # weight_compare.generate_data_handle()
  199.     # 生成随机数
  200.     # weight_compare.generate_data_random(batch_size=30, p_lb=0, p_ub=100)
  202.     # 生成偏态分布
  203.     weight_compare.generate_data_skewness(batch_size=20)
  205.     weight_compare.run(iter_num=50)
  207.     # weight_compare.plot_iteration()
  209.     # weight_compare.plot_figure()
  211.     weight_compare.plot_figure_subplot()

结果展示

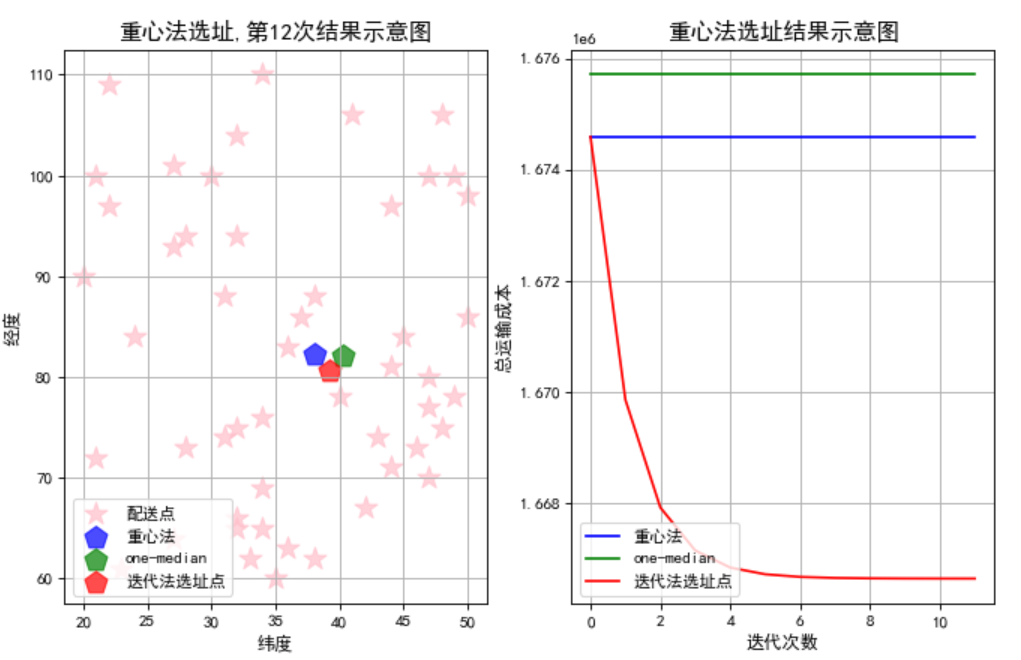
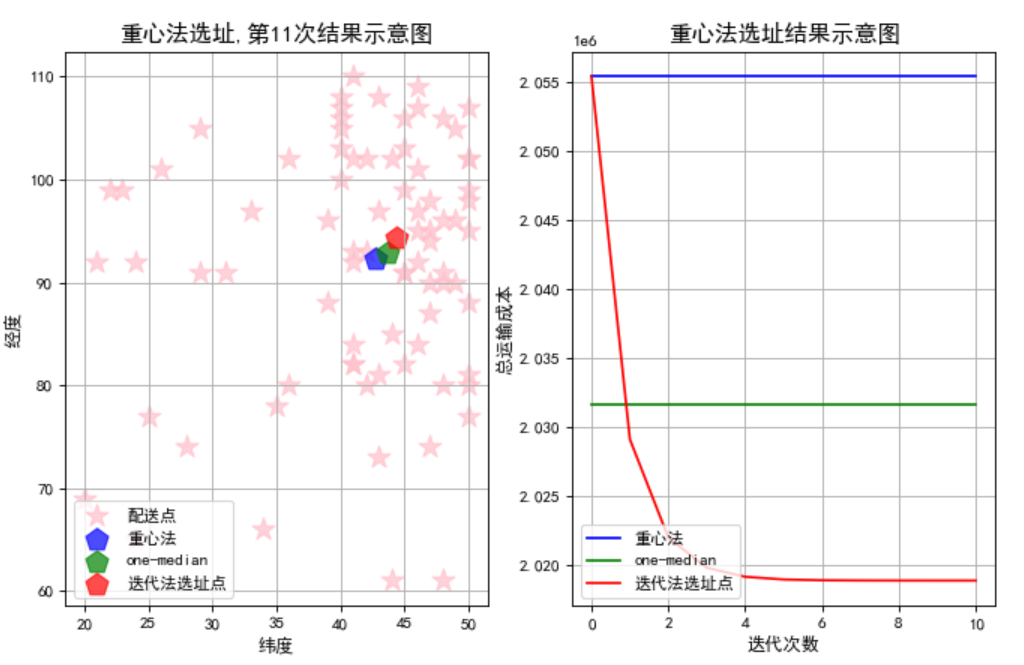
image.pngimage.png
数据为随机分布的结果 数据为偏态分布的结果

注：应该重负做100次试验，比较成本的统计结果