1. 第三问

1.1 变量

符号	含义
	每一批接到乘客的出租车数
	停车区的总长度
	出租车的长度
	左右车道上出租车中线的间距
	出租车的前后间距
	排队乘客的距离
	机场对出租车的最高限速
	出租车的速度
	乘客步行的速度
	乘客到达出租车后上车所需时间
	出租车离场所需时间
	乘客走到出租车所需时间
	前一辆出租车开动后，后一辆出租车开动的反应时间
	每一个周期的总时间
	该排队系统的效率

1.2 模型

分批入场的流程图如下：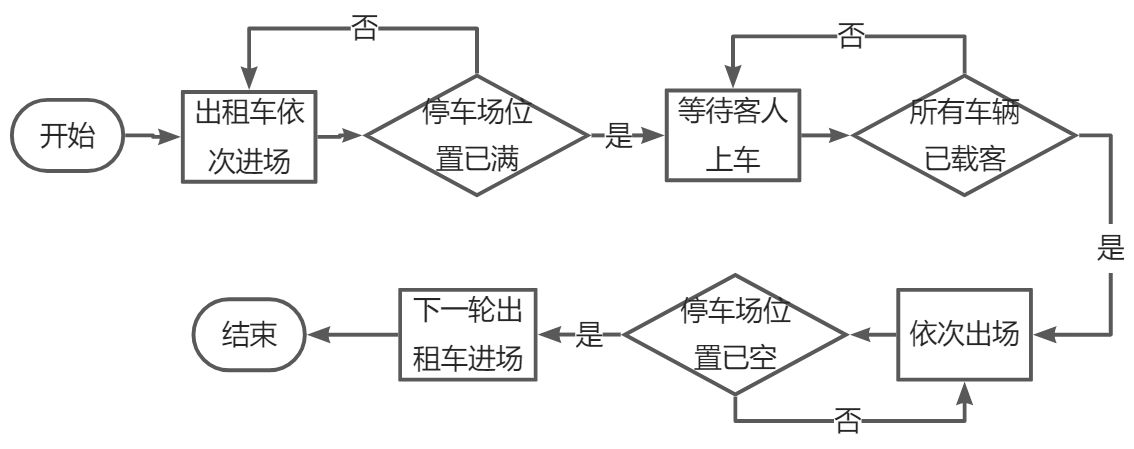

假设乘客和出租车都在排队，每一位乘客搭乘一辆出租车，且队伍是连续的，即不会出现没有乘客或没有出租车的情况。假设所有乘客的间距、所有出租车的间距相同，乘客的长度可忽略，而车长都相等且不可忽略。机场内车限速较低，可以假设出租车匀速，开动时车队速度为。乘客在上车点处排队，出租车在并行车道排队。
我们用单位时间接到乘客的出租车数来衡量该排队系统的效率。该效率是由每次入场的乘客数决定的。当每次入场的乘客数较多时，最后一名乘客从队伍末尾走到上车点的时间长，从上车点走到最远可搭乘的出租车的时间长，下一批出租车开到车队之首接乘客的距离长；而当每次入场的乘客数较少时，车队需要以更高地频率每次前进更短的距离，同样可能降低效率。此外，本题中有两个车道，因此出租车离场时有机会变道，会减缓车队整体的速度，且车队越长，变道的车总数越多，对车队整体的速度影响越大。仿照交通流理论中的 Greenberg 对数模型，我们提出车速与车队长度的关系：

1.2.1 两车道对称式分布

考虑到车道停车区的对称性，在两侧车道的中点处都设置一个上车点，让乘客走到最远的出租车的距离最短，这样花费在步行上的时间尽可能短。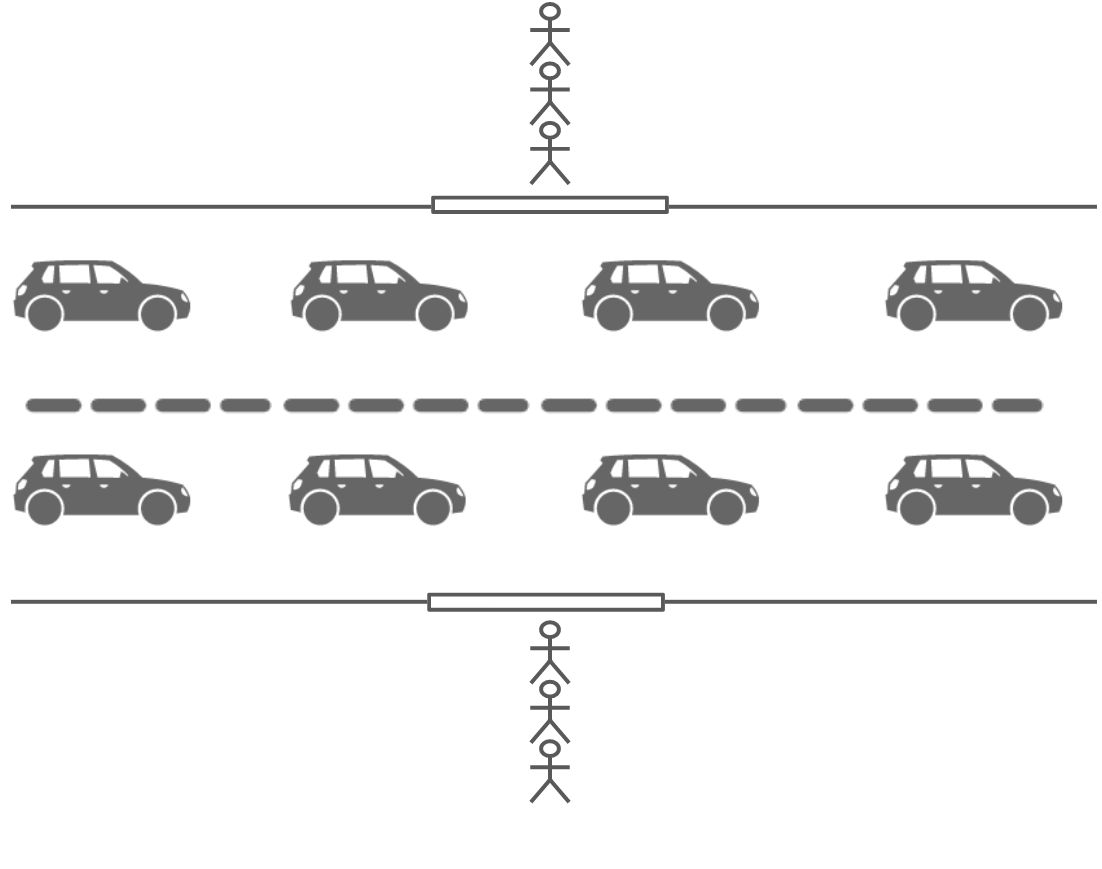

参数互相影响的关系如下图所示：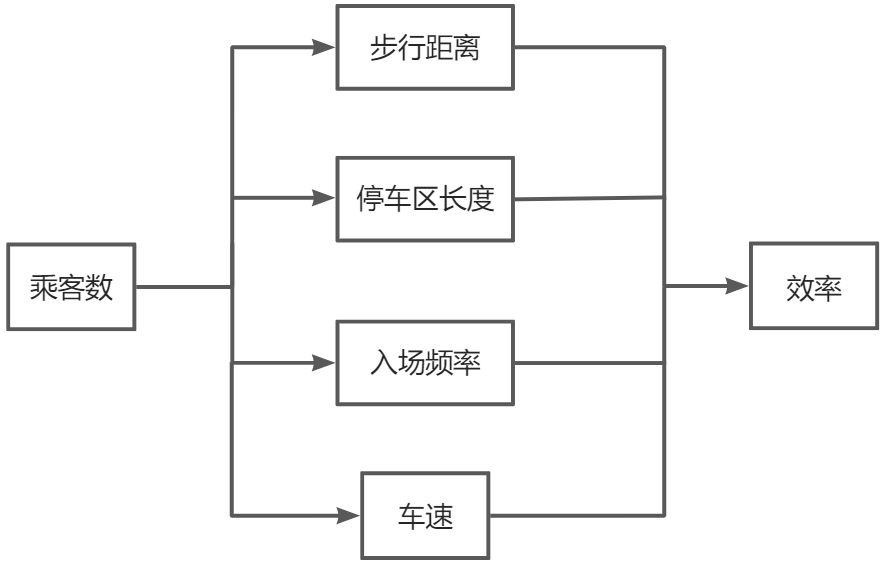

1.2.2 地铁式分布

考虑到地铁前后各设置一个上车点（车门）的设计有助于提高乘客上车效率，我们仿照其设计，在一侧车道的前后各设置一个上车点。假设乘客会优先选择离自己最近的空出租车，则下图中左右两侧的乘客会分别选择本侧的车，那么把前后上车点分别放置在两个四等分点处，乘客走到本侧最远的出租车的距离最短。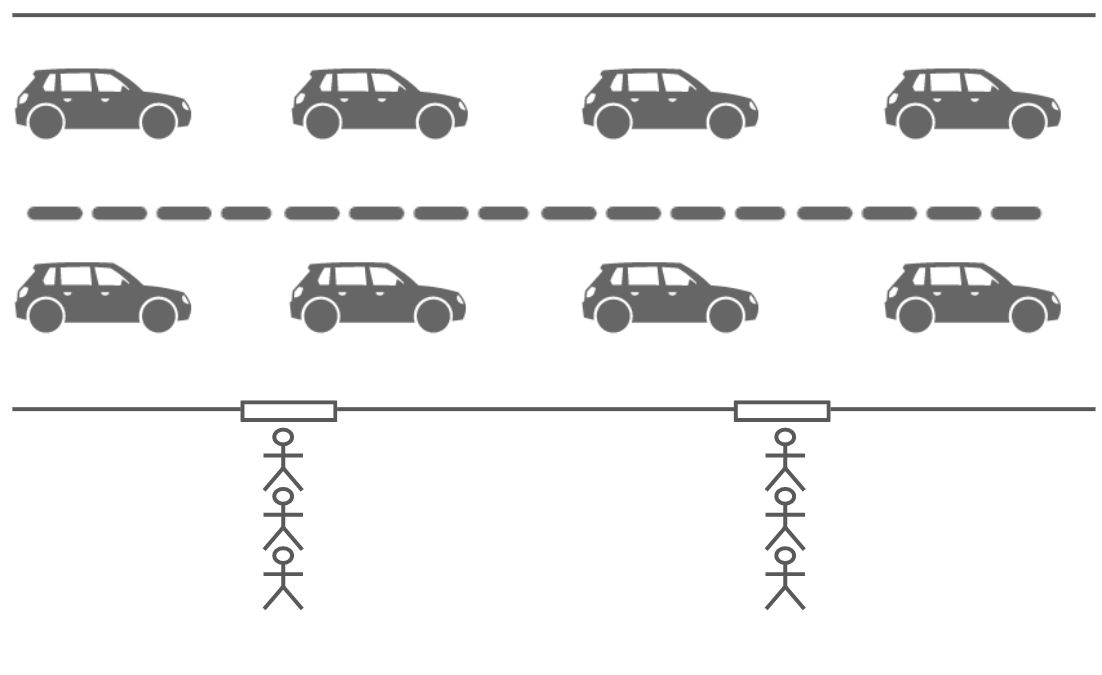

参数互相影响的关系如下图所示：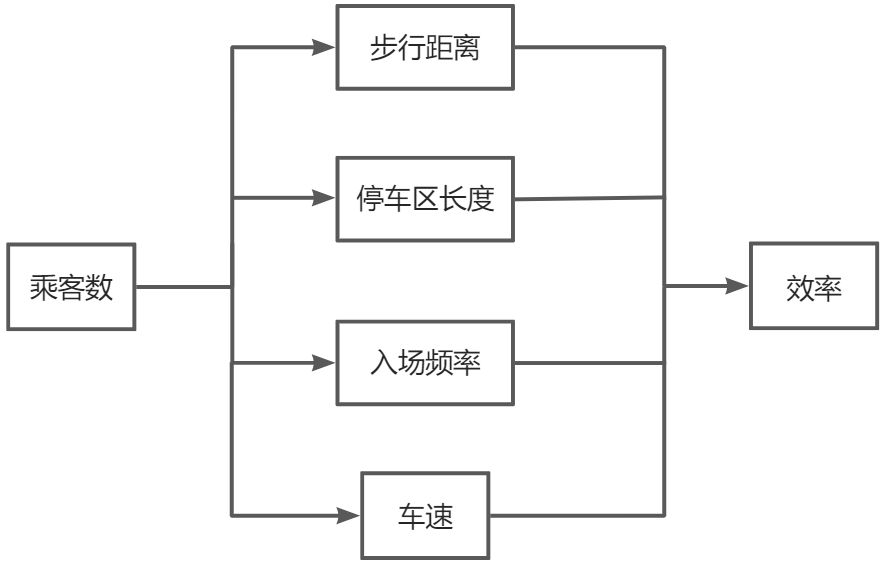

1.3 规划

1.3.1 两车道对称式分布

每一批乘客上车的时间等于最后一位上车的乘客所需时间，最后一位上车的乘客从乘客队伍最末端走到本侧车道最远的出租车，满足：

一批入场的出租车一共辆，因此换场时，从前一批的第一辆出租车开动到最后一辆出租车开动所需的反应时间为。同理，后一批出租车入场时所需的反应时间也如此。
每一批出租车离场与入场，都需要花一定时间开过停车区的长度，其时间满足：

同时，要保证停车区内的所有出租车之间、最后一辆出租车到停车区的后门之间、第一辆出租车到停车区前门之间，都要保持安全距离，所以停车区的长度满足满足：

因此，每一批乘客入场消耗的时间为，可以让辆出租车接到客人，本题的数学规划形式可写为：

与的函数关系图像类似下图，可通过求导求出最大值点。

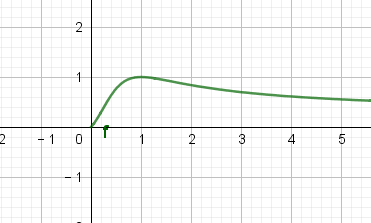
1.3.2 地铁式分布

每一批乘客上车的时间等于最后一位上车的乘客所需时间，最后一位上车的乘客先沿直线从乘客队伍最末端最前端，再沿直线走到本侧最远的出租车，满足：

其余约束条件与 1.3.1 相同。因此，写成数学规划的形式如下：