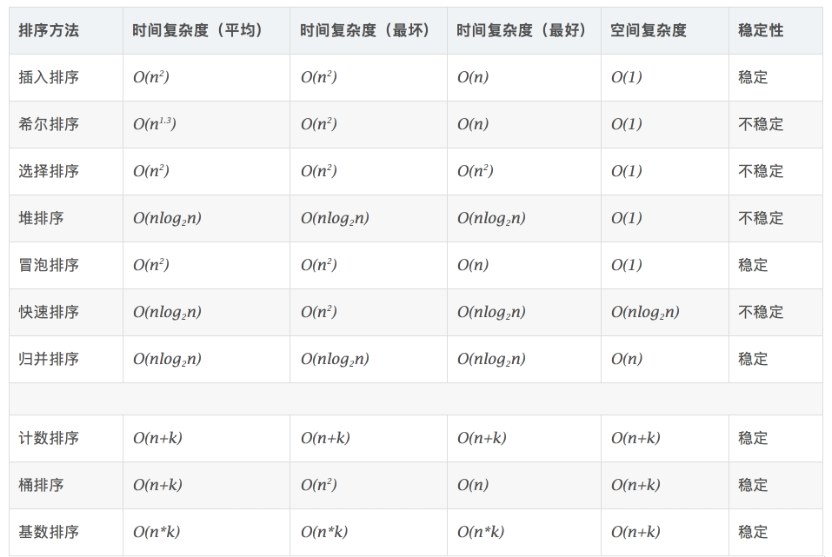
1. 各种排序的时间复杂度分析

2. 快速排序

2.1 思路

首先选取游标为,从数组高位遍历—,遇到停止，并将当前值赋值到
从数组低位遍历++,遇到停止，并将当前值赋值到
最后将的值赋予,并返回游标的位置

然后递归分区排序

2.2 代码

  public int patition(int[] a, int low, int high) {
      int pro = a[low];
      while (low < high) {
          while (low < high & a[high] > pro) high--;
          a[low] = a[high];
          while (low < high & a[low] < pro) low++;
          a[high] = a[low];
      }
      a[low] = pro;
      return low;
  }
  public void quickSort(int[] a, int low, int high) {
      int p;
      if (low < high) {
          p = patition(a, low, high);
          quickSort(a, low, p - 1);
          quickSort(a, p + 1, high);
      }
  }

3. 归并排序

3.1 思路

首先找到数组中点分别递归
然后合并左右两部分
合并过程中排序

最后递归完成总排序

3.2 代码

  public static void mergeSort(int[] data) {
      sort(data, 0, data.length - 1);
  }
  public static void sort(int[] data, int left, int right) {
      if (left >= right)
          return;
      int center = (left + right) / 2;
      sort(data, left, center);
      sort(data, center + 1, right);
      merge(data, left, center, right);
  }
  public static void merge(int[] data, int left, int center, int right) {
      int[] tmpArr = new int[data.length];
      int mid = center + 1;
      int third = left;
      int tmp = left;
      while (left <= center && mid <= right) {
          if (data[left] <= data[mid]) {
              tmpArr[third++] = data[left++];
          } else {
              tmpArr[third++] = data[mid++];
          }
      }
      while (mid <= right) {
          tmpArr[third++] = data[mid++];
      }
      while (left <= center) {
          tmpArr[third++] = data[left++];
      }
      while (tmp <= right) {
          data[tmp] = tmpArr[tmp++];
      }
  }

4. 堆排序

4.1 思路

调整堆过程:找到数组中元素i的左右节点分别是,并且判断
如果为真，交换i与最大值位置，并且进行调整堆重复1的过程。

堆排序过程就是从堆头取出元素放到数组最后一位，之后不断递归的调整堆，直到完成排序。

4.2 代码

public void heapSort(int[] arr) throws Exception {
      //对arr进行拷贝，不改变参数内容
      int len = arr.length;
      buildMaxHeap(arr, len);
      for (int i = len - 1; i > 0; i--) {
          swap(arr, 0, i);
          len--;
          heapify(arr, 0, len);
      }
  }

  private void buildMaxHeap(int[] arr, int len) {
      for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
          heapify(arr, i, len);
      }
  }

  private void heapify(int[] arr, int i, int len) {
      int left = 2 * i + 1;
      int right = 2 * i + 2;
      int largest = i;

      if (left < len && arr[left] > arr[largest]) {
          largest = left;
      }

      if (right < len && arr[right] > arr[largest]) {
          largest = right;
      }

      if (largest != i) {
          swap(arr, i, largest);
          heapify(arr, largest, len);
      }
  }

  private void swap(int[] arr, int i, int j) {
      int temp = arr[i];
      arr[i] = arr[j];
      arr[j] = temp;
  }

5. 冒泡排序

5.1 思路

5.2 代码

 public void BufferSort(int[] a) {
      int n = a.length;
      for (int i = 0; i < n; i++) {
          for (int j = 0; j < n - i - 1; j++) {
              if (a[j + 1] < a[j]) {
                  int temp = a[j + 1];
                  a[j + 1] = a[j];
                  a[j] = temp;
              }
          }
      }
  }

6. 插入排序

6.1 思路

6.2 代码

 public void insertSort(Comparable[] arr) {
      int n = arr.length;
      for (int i = 0; i < n; i++) {
          // 寻找元素 arr[i] 合适的插入位置
          for (int j = i; j > 0; j--)
              if (arr[j].compareTo(arr[j - 1]) < 0)
                  swap(arr, j, j - 1);
              else
                  break;
      }
  }

  //核心代码---结束
  private static void swap(Object[] arr, int i, int j) {
      Object t = arr[i];
      arr[i] = arr[j];
      arr[j] = t;
  }

7. 选择排序

7.1 思路

7.2 代码

  public void selectSort(int[] a) {
      int n = a.length;
      for (int i = 0; i < n - 1; i++) {
          for (int j = i + 1; j < n; j++) {
              if (a[j] < a[i]) {
                  int temp = a[i];
                  a[i] = a[j];
                  a[j] = temp;
              }
          }
      }
  }