家乐的深度学习笔记「5」 - 多层感知机

背景

由于前文提到的包括线性回归和softmax回归在内的单层神经网络均只能解决线性分类问题，一个常见的反例就是异或（XOR）问题，假设坐标轴上有四个点：

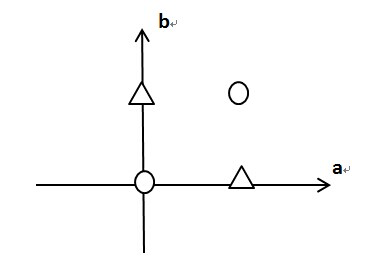
这样的四个点，在平面上划一条直线（线性分类模型），是无论如何都没有办法将圆形和三角形分开的。这个问题从直观上很好理解，要证明这一点首先需要一个概念，即数据集的线性可分性：

给定一个数据集：

其中，如果存在某个超平面：使得

能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，则称数据集为线性可分数据集。

由此，我们可以证明以下定理，其中凸壳即凸包，是实数向量空间中，对于给定集合，所有包含X的凸集的交集，通俗理解为一条刚好包着所有点的橡皮圈，其求取算法在文章下的参考资料里有说明（格雷哈姆算法）：

样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点所构成的凸壳互不相交。

这里引用一段别人的证明，自己实在写不出充分性的证明文字：

必要性： 假设样本集T线性可分，则存在一个超平面 将数据集的正实例点和负实例点完全正确地划分到 的两侧。显然两侧的点分别构成的凸壳不相交； 充分性： 假设存在两个凸壳A、B相交，且存在超平面 将A和B线性分割。令A在B的凸壳内部的点为a，因为线性可分，则A中不存在两点之间的连线与超平面 相交，而凸壳B中任意一点与A中的点的连线均与超平面 相交，则B内部的点a也与A中任一点之间的连线不与 相交，与A中不存在两点之间的连线与超平面小脚矛盾。故只有正负实例点所构成的两个凸壳不相交时样本集才线性可分。

于是一大票工程师就傻了，最简单的异或问题都解决不了，而生活中到处常见此类问题，这还学什么神经网络，赶紧扔掉，这样神经网络就被搁置了一段时间，直到多层感知机的提出，至于其他问题都是后话了，详见文章下的参考资料（历史部分），本文主要介绍多层感知机的由来、原理以及实现，常见的激活函数等内容。

多层感知机

多层感知机（MLP），也叫前馈神经网络（FNN），是人工智能领域中最早发明的简单人工神经网络类型，FNN由一个输入层、一个（浅层网络）或多个（深层网络，因此叫作深度学习）隐藏层，和一个输出层构成。每个层（除输出层以外）与下一层连接。这种连接是 FNN 架构的关键，具有两个主要特征：加权平均值和激活函数。

MLP是一种前向结构的人工神经网络，可以被看作是一个有向图，由多个的节点层所组成，每一层都全连接到下一层。除了输入节点，每个节点都是一个带有非线性激活函数的神经元（或称处理单元），是单层感知器的推广，克服了感知器不能对线性不可分数据进行识别的弱点。

加权平均值

因为MLP的每一层都是全连接层（除了输入层），所以每一层节点值的计算除了计算自己的权重之外，还需要根据前一层所有节点的加权总和激活，即每个连接点的权重乘以该节点的激活函数的总和。每个节点仅从前一层获取输入值，因此权重是同一层中节点的唯一区分依据。

激活函数

背景导入

为了理解激活函数的意义，先让我们简单构建一个隐藏层也是全连接层的神经网络：

具体来说，给定一个小批量样本，其批量大小为，输入个数为。假设多层感知机只有一个隐藏层，其中隐藏单元个数为。记隐藏层的输出（也称为隐藏层变量或隐藏变量）为，有。因为隐藏层和输出层均是全连接层，可以设隐藏层的权重参数和偏差参数分别为和，输出层的权重和偏差参数分别为和。

我们先来看一种含单隐藏层的多层感知机的设计。其输出的计算为：

也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来，可以得到

从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为，偏差参数为。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

那咋办呢？隐藏层是不是没用呢？徒增了计算，结果还和原来的网络等价？

上面的问题根源就是每层依然是全连接，而全连接层只是对数据做仿射变换，多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法就是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数就是本节要讲的激活函数：

ReLU函数

ReLU（rectified linear unit）函数提供了一个很简单的非线性变换。给定元素，该函数定义为：

可以看出，ReLU函数只保留正数元素，并将负数元素清零，其函数图像如下：

显然，当输入为负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1。尽管输入为0时ReLU函数不可导，但可以取此处的导数为0，画出其导数图像：

sigmoid函数

这个函数就是高中生物说的S型函数了，是不是有种似曾相识的感觉。它有着良好的性质：单增且反函数单增、平滑易于求导；在神经网络中常作为隐层的激活函数，可以将实数映射到区间上：

S函数在早起的神经网络中较为普遍，但是逐渐被更简单的ReLU函数取代。利用它的值域在0到1之间这一特性可以控制信息在神经网络中的流动。当输入接近0时，S函数接近线性变换：

依据链式法则，S函数的导数为：

当输入为0时，S函数的导数达到最大值0.25，当输入越偏离0时，S函数的导数越接近0：

tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：

当输入接近0时，tanh也接近线性变换，虽然这个函数和S函数的形状很像，但是它在坐标系的原点上对称：

根据链式法则，tanh函数的导数为：

当输入为0时，tanh函数的导数达到最大值1；当输入越偏离0是，tanh函数的导数越接近0：

当隐藏层使用非线性的激活函数时，其按照以下方式输出：

其中表示激活函数。在分类问题中，可以对输出做softmax运算，并使用softmax回归中的交叉熵损失函数；在回归问题中，可以将输出层的输出个数设为1，并将输出直接提供给线性回归中使用的平方损失函数。

有了激活函数的定义以后，MLP的定义就可以更近一步的理解：MLP在输出层与输入层之间加入了一个或多个隐藏层，并通过激活函数对隐藏层输出进行变换。

通用近似定理

通用近似定理，又名万能逼近定理，即含有大于等于一个隐藏层的神经网络理论上就可以拟合所有函数，又因为多个隐藏层在训练时易发生梯度消失的情况，所以大多数情况下MLP的实现只需要一个隐藏层即可。在下面的简洁实现中可以看到增加或减少隐藏层节点数，以及增大隐藏层层数的效果。

多层感知机的从零实现

导入需要的库

from mxnet.gluon import loss as gloss
from mxnet import autograd, gpu, nd
import d2lzh as d2l

指定GPU

ctx = gpu(3)

加载数据集

这部分在前文已经有了详细的叙述。

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

定义模型参数

这里注意每一层输入与输出的关系，从这里看每个神经元和之前也没有什么区别，事实上本来也没有什么区别，都是全连接层，区别仅在计算方法上由简单的线性加和变成了非线性的激活函数。

num_inputs, num_outputs, num_hiddens = 28 * 28, 10, 256
W1 = nd.random.normal(scale=0.01, shape=(num_inputs, num_hiddens), ctx=ctx)
b1 = nd.zeros(num_hiddens, ctx=ctx)
W2 = nd.random.normal(scale=0.01, shape=(num_hiddens, num_outputs), ctx=ctx)
b2 = nd.zeros(num_outputs, ctx=ctx)
params = [W1, b1, W2, b2]
for param in params:
    param.attach_grad()

激活函数

使用常见的ReLU函数作为隐藏层的激活函数，具体函数已经在上面说过了。

def relu(X):
    return nd.maximum(X, 0)

定义模型

同样将输入图像展开为一个直向量，使用激活函数来计算隐藏层结果。

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(nd.dot(X, W1) + b1)
    return nd.dot(H, W2) + b2

定义损失函数

前文说过直接采用gluon提供的这个函数具有更好的数值稳定性。

loss = gloss.SoftmaxCrossEntropyLoss()

计算准确性

这是前文函数的稍微改进版，具体最终版在下面的简洁实现里介绍。

def evaluate_accuracy(data_iter, net, ctx):
    acc_sum, n = nd.array([0], ctx=ctx), 0
    for X, y in data_iter:
        X = X.as_in_context(ctx)
        y = y.as_in_context(ctx)
        y = y.astype('float32')
        acc_sum += (net(X).argmax(axis=1) == y).sum()
        n += y.size
        acc_sum.wait_to_read()
    return acc_sum.asscalar() / n

优化算法

依然是sgd（随机小批量）。

def sgd(params, lr, batch_size):
    for param in params:
        param[:] = param - lr * param.grad / batch_size

训练模型

定义好超参数，就可以开始炼丹了（误

num_epochs, lr = 10, 0.5
def train(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            X = X.as_in_context(ctx)
            y = y.as_in_context(ctx)
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            sgd(params, lr, batch_size)
            y = y.astype('float32')
            train_l_sum += l.asscalar()
            train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n += y.size
        test_acc = evaluate_accuracy(test_iter, net, ctx)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)

可以和上文softmax回归对比一下，效果比其稍微好了这么一点。

epoch 1, loss 0.7850, train acc 0.707, test acc 0.811
epoch 2, loss 0.4918, train acc 0.818, test acc 0.847
epoch 3, loss 0.4290, train acc 0.842, test acc 0.859
epoch 4, loss 0.3929, train acc 0.854, test acc 0.865
epoch 5, loss 0.3704, train acc 0.864, test acc 0.865
epoch 6, loss 0.3503, train acc 0.871, test acc 0.874
epoch 7, loss 0.3393, train acc 0.875, test acc 0.879
epoch 8, loss 0.3234, train acc 0.881, test acc 0.870
epoch 9, loss 0.3150, train acc 0.885, test acc 0.879
epoch 10, loss 0.3081, train acc 0.886, test acc 0.880

全部代码

多层感知机的从零实现.html

多层感知机的简洁实现

导入需要的库

from mxnet.gluon import loss as gloss, utils as gutils, nn
from mxnet import autograd, gluon, init, nd
import mxnet as mx
import time

多GPU训练

这个就是寻找GPU函数的最终版本了，可以直接用在其他炼丹项目中。

# [Cell可独立] 多GPU训练第一步：找到你的GPU
def try_all_gpus():
    import mxnet as mx
    ctxes = []
    try:
        for i in range(16):
            ctx = mx.gpu(i)
            _ = mx.nd.array([0], ctx=ctx)
            ctxes.append(ctx)
    except mx.base.MXNetError:
        pass
    if not ctxes:
        ctxes = [mx.cpu()]
    return ctxes
ctx = try_all_gpus()

加载数据集

这里去掉了d2lzh库的依赖，改为自己加载，以后做的模型也会慢慢去掉d2lzh这个依赖，更多的尝试自己构建出一个适合自己的工具包。另外这个函数为了可以独立于使用，把部分import写在了里面，因为不需要循环执行，所以对性能的影响基本上可以忽略，主要是为了防自己没导入，浪费重新调整的时间。

# [Cell可独立] 加载Fashion_MNIST数据集
def get_fashion_mnist(batch_size=256, num_workers=40):
    from mxnet.gluon import data as gdata
    mnist_train = gdata.vision.FashionMNIST(train=True)
    mnist_test = gdata.vision.FashionMNIST(train=False)
    transformer = gdata.vision.transforms.ToTensor()
    import sys
    if sys.platform.startswith('win'):
        num_workers = 0
    train_iter = gdata.DataLoader(mnist_train.transform_first(transformer),
                                 batch_size=batch_size, shuffle=True,
                                 num_workers=num_workers)
    test_iter = gdata.DataLoader(mnist_test.transform_first(transformer),
                                batch_size=batch_size, shuffle=False,
                                num_workers=num_workers)
    return train_iter, test_iter
train_iter, test_iter = get_fashion_mnist()

定义模型

有了gluon，定义模型就变的很简单了，想加多少层加多少层，改改参数即可。

net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)

定义损失函数及优化算法

loss = gloss.SoftmaxCrossEntropyLoss()
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})

拆分特征和标签到多GPU上

为了多GPU评测作准备。

def _get_batch(batch, ctx):
    features, labels = batch
    if labels.dtype != features.dtype:
        labels = labels.astype(features.dtype)
    return (gutils.split_and_load(features, ctx),
            gutils.split_and_load(labels, ctx), features.shape[0])

在多GPU上同时评测模型

加速评测，GPU都利用起来，实测每个显存占用还不到1G。

def evaluate_accuracy(data_iter, net, ctx=[mx.cpu()]):
    if isinstance(ctx, mx.Context):
        ctx = [ctx]
    acc_sum, n = nd.array([0]), 0
    for batch in data_iter:
        features, labels, _ = _get_batch(batch, ctx)
        for X, y in zip(features, labels):
            y = y.astype('float32')
            acc_sum += (net(X).argmax(axis=1) == y).sum().copyto(mx.cpu())
            n += y.size
        acc_sum.wait_to_read()
    return acc_sum.asscalar() / n

训练模型

铺垫了这么多，终于可以开始炼丹了。

num_epochs = 5
def train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs):
    print('training on', ctx)
    if isinstance(ctx, mx.Context):
        ctx = [ctx]
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n, m, start = 0.0, 0.0, 0, 0, time.time()
        for i, batch in enumerate(train_iter):
            Xs, ys, batch_size = _get_batch(batch, ctx)
            with autograd.record():
                y_hats = [net(X) for X in Xs]
                ls = [loss(y_hat, y) for y_hat, y in zip(y_hats, ys)]
            for l in ls:
                l.backward()
            trainer.step(batch_size)
            train_l_sum += sum([l.sum().asscalar() for l in ls])
            n += sum([l.size for l in ls])
            train_acc_sum += sum([(y_hat.argmax(axis=1) == y).sum().asscalar()
                                 for y_hat, y in zip(y_hats, ys)])
            m += sum([y.size for y in ys])
        test_acc = evaluate_accuracy(test_iter, net, ctx)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, '
              'time %.1f sec'
              % (epoch + 1, train_l_sum / n, train_acc_sum / m, test_acc,
                 time.time() - start))
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

四个GPU的情况下，一轮大概是4秒左右，可以看到loss还是挺大的，仍有不少训练空间。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 0.7741, train acc 0.712, test acc 0.811, time 3.6 sec
epoch 2, loss 0.4870, train acc 0.819, test acc 0.839, time 3.7 sec
epoch 3, loss 0.4293, train acc 0.840, test acc 0.826, time 3.8 sec
epoch 4, loss 0.3955, train acc 0.853, test acc 0.847, time 3.6 sec
epoch 5, loss 0.3738, train acc 0.861, test acc 0.855, time 3.8 sec

全部代码

多层感知机的简洁实现.html

书后练习

增大隐层的神经元数量

# 增大隐层的神经元数量
net = nn.Sequential()
net.add(nn.Dense(1024, activation='relu'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

可以看到，训练速度稍微变慢了一点，整体效果和原来差不多。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 0.7801, train acc 0.709, test acc 0.771, time 3.7 sec
epoch 2, loss 0.4785, train acc 0.822, test acc 0.829, time 3.9 sec
epoch 3, loss 0.4256, train acc 0.843, test acc 0.824, time 5.2 sec
epoch 4, loss 0.3848, train acc 0.859, test acc 0.855, time 3.8 sec
epoch 5, loss 0.3629, train acc 0.866, test acc 0.855, time 3.8 sec

减少隐层的神经元数量

# 减少隐层的神经元数量
net = nn.Sequential()
net.add(nn.Dense(128, activation='relu'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)
num_epochs = 5
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

可以看到，模型收敛速度明显更慢了。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 0.7997, train acc 0.699, test acc 0.786, time 3.5 sec
epoch 2, loss 0.4947, train acc 0.817, test acc 0.834, time 3.4 sec
epoch 3, loss 0.4321, train acc 0.840, test acc 0.749, time 3.4 sec
epoch 4, loss 0.4024, train acc 0.851, test acc 0.859, time 3.5 sec
epoch 5, loss 0.3773, train acc 0.860, test acc 0.837, time 3.5 sec

增大隐层的层数

# 增大隐层的层数
net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'),
        nn.Dense(256, activation='relu'),
        nn.Dense(256, activation='relu'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

可以看到，训练时间明显增加了，模型收敛的也更慢。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 1.8822, train acc 0.244, test acc 0.401, time 4.3 sec
epoch 2, loss 0.8444, train acc 0.661, test acc 0.575, time 4.3 sec
epoch 3, loss 0.6710, train acc 0.740, test acc 0.777, time 4.2 sec
epoch 4, loss 0.5123, train acc 0.810, test acc 0.804, time 4.3 sec
epoch 5, loss 0.4501, train acc 0.833, test acc 0.853, time 4.3 sec

再增大隐层的层数

# 再增大隐层的层数
net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'),
        nn.Dense(256, activation='relu'),
        nn.Dense(256, activation='relu'),
        nn.Dense(256, activation='relu'),
        nn.Dense(256, activation='relu'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

可以看到，模型梯度消失了，压根不收敛，直接爆炸了。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 2.3031, train acc 0.098, test acc 0.100, time 5.2 sec
epoch 2, loss 2.3031, train acc 0.100, test acc 0.100, time 5.3 sec
epoch 3, loss 2.3030, train acc 0.100, test acc 0.100, time 5.3 sec
epoch 4, loss 2.3031, train acc 0.100, test acc 0.100, time 5.3 sec
epoch 5, loss 2.3030, train acc 0.101, test acc 0.100, time 5.2 sec

试一下sigmoid激活函数

# 试一下sigmoid激活函数
net = nn.Sequential()
net.add(nn.Dense(256, activation='sigmoid'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

不同激活函数的效果其实具有一定的随机性，现在的我还解释不过来。至少多次运行之后，结果会有挺大的差异。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 1.0438, train acc 0.616, test acc 0.761, time 3.6 sec
epoch 2, loss 0.5768, train acc 0.784, test acc 0.779, time 3.5 sec
epoch 3, loss 0.5045, train acc 0.816, test acc 0.823, time 3.7 sec
epoch 4, loss 0.4708, train acc 0.828, test acc 0.817, time 3.6 sec
epoch 5, loss 0.4476, train acc 0.838, test acc 0.847, time 3.4 sec

试一下tanh激活函数

# 试一下tanh激活函数
net = nn.Sequential()
net.add(nn.Dense(256, activation='tanh'),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01), ctx=ctx)
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.5,
})
train(train_iter, test_iter, net, loss, trainer, ctx, num_epochs)

不同激活函数的效果其实具有一定的随机性，现在的我还解释不过来。至少多次运行之后，结果会有挺大的差异。

training on [gpu(0), gpu(1), gpu(2), gpu(3)]
epoch 1, loss 4.2582, train acc 0.561, test acc 0.706, time 3.4 sec
epoch 2, loss 1.2286, train acc 0.734, test acc 0.754, time 3.5 sec
epoch 3, loss 0.8186, train acc 0.779, test acc 0.798, time 3.5 sec
epoch 4, loss 0.6507, train acc 0.804, test acc 0.798, time 3.5 sec
epoch 5, loss 0.5751, train acc 0.818, test acc 0.754, time 3.5 sec

参考资料

前馈神经网络｜机器之心
12. 深度学习（1）：多层感知机
统计学习方法 —— 感知机（异或问题的证明）
机器学习-白板推导系列(二十三)-前馈神经网络（Feedforward Neural Network）：
点击查看【bilibili】

二维凸包的格雷哈姆扫描算法（Graham）：
点击查看【bilibili】