决策树（Decision Tree）

是有监督学习中的一种算法，并且是一种基本的分类与回归的方法。也就是说，决策树有 两种：分类树和回归树。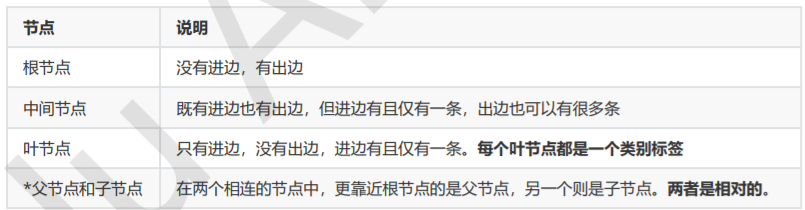
image.png
我们可以把决策树看作是一个if-then规则的集合。将决策树转换成if-then规则的过程是这样的：

  • 由决策树的根节点到叶节点的每一条路径构建一条规则
  • 路径上中间节点的特征对应着规则的条件，也叶节点的类标签对应着规则的结论

决策树的路径或者其对应的if-then规则集合有一个重要的性质：互斥并且完备。也就是说，每一个实例都被有且仅有一条路径或者规则所覆盖。这里的覆盖是指实例的特征与路径上的特征一致，或实例满足规则的条件

决策树的构建准备工作

首先我们要收集足够多的数据，如果数据收集不到位，将会导致没有足够的特征去构建错误率低的决策树。数据特征充足，但是不知道用哪些特征好，也会导致最终无法构建出分类效果好的决策树。
概括为3个步骤：特征选择、决策树的生成和决策树的剪枝

特征选择

  • 特征选择就是决定用哪个特征来划分特征空间，其目的在于选取对训练数据具有分类能力的特征
  • 一般而言，随着划分过程不断进行，我们希望决策树的分支节点所包含的样本 尽可能属于同一类别，也就是节点的纯度（purity）越来越高
  • 在实际使用中，我们衡量的常常是不纯度。度量不纯度的指标有很多种，比如：熵、增益率、基尼指数。 这里我们使用的是熵，也叫作香农熵，这个名字来源于信息论之父 克劳德·香农。

    香农熵及计算函数

    image.png

    信息增益

    信息增益（Information Gain）的计算公式其实就是父节点的信息熵与其下所有子节点总信息熵之差。但这里要注 意的是，此时计算子节点的总信息熵不能简单求和，而要求在求和汇总之前进行修正。

image.png

数据集最佳切分函数

划分数据集的最大准则是选择最大信息增益，也就是信息下降最快的方向

  1. """
  2. 函数功能：根据信息增益选择出最佳数据集切分的列
  3. 参数说明：
  4. dataSet：原始数据集
  5. 返回：
  6. axis:数据集最佳切分列的索引
  7. """
  8. #选择最优的列进行切分
  9. def bestSplit(dataSet):
  10.     baseEnt = calEnt(dataSet) #计算原始熵
  11.     bestGain = 0 #初始化信息增益
  12.     axis = -1 #初始化最佳切分列，标签列
  13.     for i in range(dataSet.shape[1]-1): #对特征的每一列进行循环
  14.         levels= dataSet.iloc[:,i].value_counts().index #提取出当前列的所有取值
  15.         ents = 0 #初始化子节点的信息熵
  16.         for j in levels: #对当前列的每一个取值进行循环
  17.             childSet = dataSet[dataSet.iloc[:,i]==j] #某一个子节点的dataframe
  18.             ent = calEnt(childSet) #计算某一个子节点的信息熵
  19.             ents += (childSet.shape[0]/dataSet.shape[0])*ent #计算当前列的信息熵
  20.     #print(f'第{i}列的信息熵为{ents}')
  21.     infoGain = baseEnt-ents #计算当前列的信息增益
  22.     #print(f'第{i}列的信息增益为{infoGain}')
  23.     if (infoGain > bestGain):
  24.         bestGain = infoGain #选择最大信息增益
  25.         axis = i #最大信息增益所在列的索引
  26.     return axis

按照给定列切分数据集

通过最佳切分函数返回最佳切分列的索引，我们就可以根据这个索引，构建一个按照给定列切分数据集的函数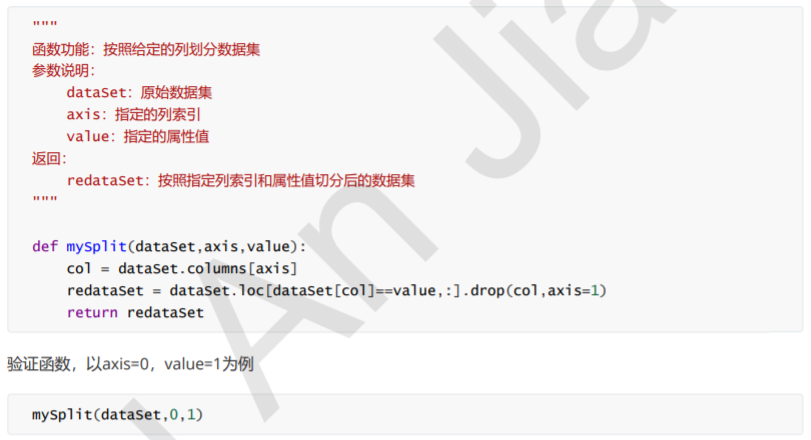
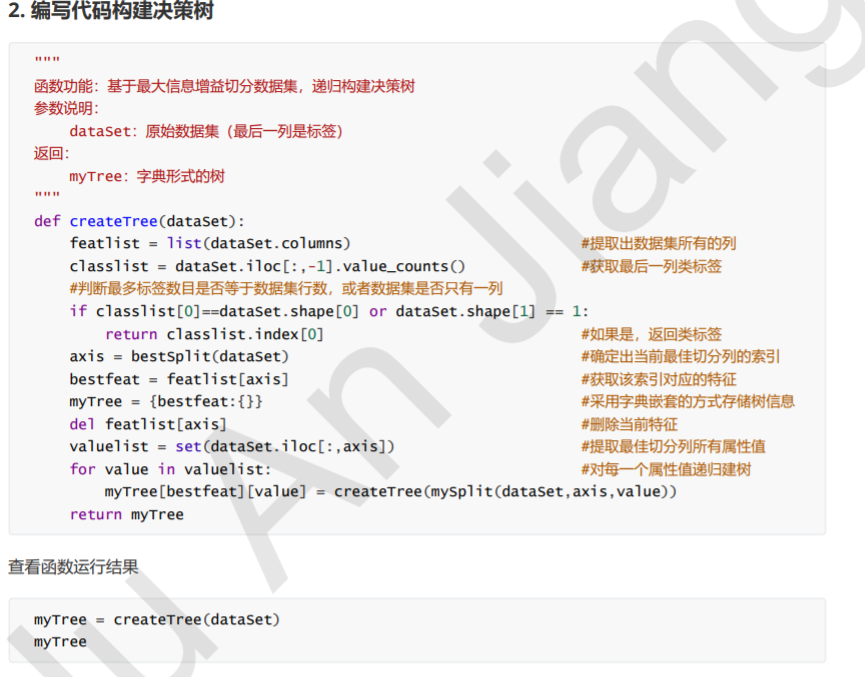
image.png

递归构建决策树

  • 工作原理如下：得到原始数据集，然后基于 最好的属性值划分数据集，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分。第一次划分之 后，数据集被向下传递到树的分支的下一个结点。在这个结点上，我们可以再次划分数据。因此我们可以采用递归 的原则处理数据集。

  • 决策树生成算法递归地产生决策树，直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确，但对未 知的测试数据的分类却没有那么准确，即出现过拟合现象。过拟合的原因在于学习时过多地考虑如何提高对训练数 据的正确分类，从而构建出过于复杂的决策树。解决这个问题的办法是考虑决策树的复杂度，对已生成的决策树进 行简化，也就是常说的剪枝处理。剪枝处理的具体讲解我会放在回归树里面。

    ID3算法

  • 构建决策树的算法有很多，比如ID3、C4.5和CART，基于《机器学习实战》这本书，我们选择ID3算法。 ID3算法的核心是在决策树各个节点上对应信息增益准则选择特征，递归地构建决策树。

  • 具体方法是：从根节点开 始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立 子节点；再对子节点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为 止。最后得到一个决策树。
  • 递归结束的条件是：程序遍历完所有的特征列，或者每个分支下的所有实例都具有相同的分类。如果所有实例具有 相同分类，则得到一个叶节点。任何到达叶节点的数据必然属于叶节点的分类，即叶节点里面必须是标签

image.png

决策树的存储

构造决策树是很耗时的任务，即使处理很小的数据集，也要花费几秒的时间，如果数据集很大，将会耗费很多计算 时间。因此为了节省时间，建好树之后立马将其保存，后续使用直接调用即可。 我这边使用的是numpy里面的save()函数，它可以直接把字典形式的数据保存为.npy文件，调用的时候直接使用 load()函数即可。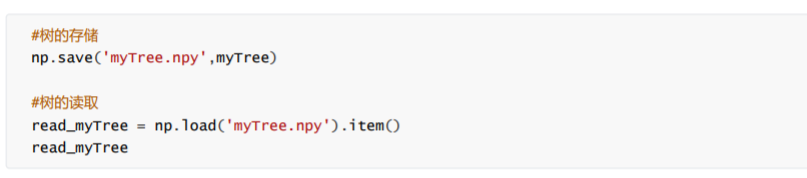
image.png

使用决策树执行分类

  1. def classify(inputTree,labels, testVec):
  2.     firstStr = next(iter(inputTree)) #获取决策树第一个节点
  3.     secondDict = inputTree[firstStr] #下一个字典
  4.     featIndex = labels.index(firstStr) #第一个节点所在列的索引
  5.     for key in secondDict.keys():
  6.         if testVec[featIndex] == key:
  7.             if type(secondDict[key]) == dict :
  8.                 classLabel = classify(secondDict[key], labels, testVec)
  9.             else:
  10.                 classLabel = secondDict[key]
  11.     return classLabel
  13. def acc_classify(train,test):
  14.     inputTree = createTree(train) #根据测试集生成一棵树
  15.     labels = list(train.columns) #数据集所有的列名称
  16.     result = []
  17.     for i in range(test.shape[0]): #对测试集中每一条数据进行循环
  18.         testVec = test.iloc[i,:-1] #测试集中的一个实例
  19.         classLabel = classify(inputTree,labels,testVec) #预测该实例的分类
  20.         result.append(classLabel) #将分类结果追加到result列表中
  21.     test['predict']=result #将预测结果追加到测试集最后一列
  22.     acc = (test.iloc[:,-1]==test.iloc[:,-2]).mean() #计算准确率
  23.     print(f'模型预测准确率为{acc}')
  24.     return test

image.png

  1. import matplotlib.pyplot as plt
  2. %matplotlib inline
  3. plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文

使用SKlearn中graphviz包实现决策树的绘制

1. 决策树的优点

决策树可以可视化，易于理解和解释；
数据准备工作很少。
其他很多算法通常都需要数据规范化，需要创建虚拟变量并删除空值等；
能够同时处理数值和分类数据，既可以做回归又可以做分类。
其他技术通常专门用于分析仅具有一种变量类 型的数据集；
效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度；
能够处理多输出问题，即含有多个标签的问题，注意与一个标签中含有多种标签分类的问题区别开；
是一个白盒模型，结果很容易能够被解释。如果在模型中可以观察到给定的情况，则可以通过布尔逻辑轻松 解释条件。相反，在黑盒模型中（例如，在人工神经网络中），结果可能更难以解释。

2. 决策树的缺点

递归生成树的方法很容易出现过拟合。 决策树可能是不稳定的，因为即使非常小的变异，可能会产生一颗完全不同的树如果某些分类占优势，决策树将会创建一棵有偏差的树。因此，建议在拟合决策树之前平衡数据集。