背包

不放i，就是dp[i][j] = dp[i - 1][j]
放i，就是 dp[i][j] = dp[i - 1][j - weight[i]] + value[i]

dp[i][j] = max(
dp[i - 1][j],
dp[i - 1][j - weight[i]] + value[i]
)

全部 dp[i][0] =0；
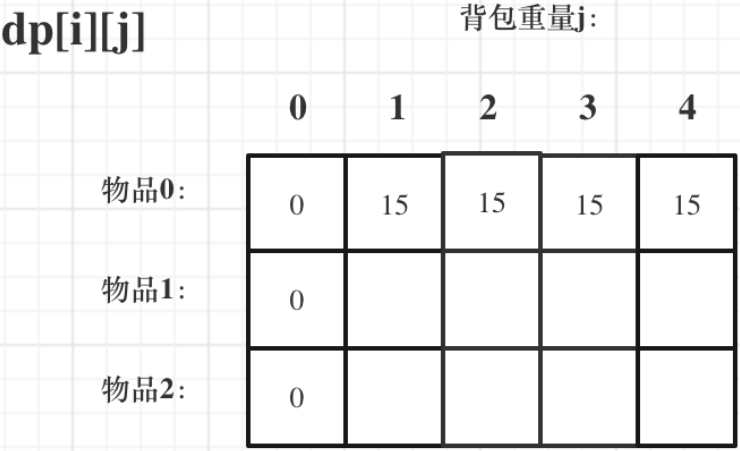
各种背包 全部j 放不放0物品时的价值最大值 肯定放最大
for (int j = weight[0]; j <= bagWeight; j++) {
dp[0][j] = value[0];
}

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}

或者先遍历背包
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}

虽然两个for循环遍历的次序不同，但是dp[i][j]所需要的数据就是左上角

dp[i][j] = max(
dp[i - 1][j],
dp[i - 1][j - weight[i]] + value[i]
);

dp[j] 可以通过 dp[j - weight[i]] 得到
即容量转移，转移前已经最大，转移后只要加上i 的价值即可

也可以不取i，那么最大值就是保持上一个物品下的最大值
dp[j] = max(
dp[j],
dp[j - weight[i]] + value[i]
);

先遍历物品嵌套遍历背包容量

01背包问的是，装满背包时，最大价值是多少
能不能装满？
能装的最大价值，尽量装但不一定满
有多少种方式能装满背包？

装满容量j，最大价值为 dpj
装满容量j，方法一共有dpj

完全背包