二叉树的遍历

基本性质

每个结点最多有两棵子树，左子树和右子树，顺序不可颠倒。

1. 非空二叉树第nn层最多有2n−12n−1个元素。
2. 深度为hh的二叉树，至多有2h−12h−1个结点。

   结点结构

   class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
   }

   二叉树的遍历

   遍历即将树的所有结点都访问且仅访问一次。按照根结点访问次序的不同，可以分为前序遍历，中序遍历，后序遍历。

• 前序遍历：根结点 -> 左子树 -> 右子树
• 中序遍历：左子树 -> 根结点 -> 右子树
• 后序遍历：左子树 -> 右子树 -> 根结点

另外还有一种层次遍历，即每一层都从左向右遍历。
例如：求下图的二叉树的遍历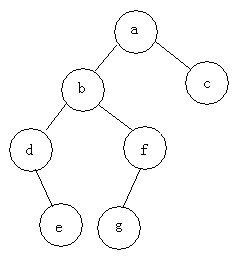

前序遍历：abdefgc
中序遍历：debgfac
后序遍历：edgfbca
层次遍历：abcdfeg

1.前序遍历

迭代法前序遍历

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while(root != null || !stack.empty()){
            while(root != null){
                result.add(root.val);
                stack.push(root);
                root = root.left;
            }
            if(!stack.empty()){
                root = stack.pop();
                root = root.right;
            }
        }
        return result;
    }  
}

递归方法前序遍历

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new LinkedList<>();
        preorderTraversalHelper(list,root);
        return list;
    }
        private static void preorderTraversalHelper(List<Integer> list, TreeNode root) {
        if (root!=null){
            list.add(root.val);
            preorderTraversalHelper(list,root.left);
            preorderTraversalHelper(list,root.right);
        }
    }
}

2 中序遍历

迭代方法实现的中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while(root != null || !stack.empty()){
            while(root != null){
                stack.push(root);
                root = root.left;
            }
            if(!stack.empty()){
                root = stack.pop();
                result.add(root.val);
                root = root.right;
            }
        }
        return result;
    }
}

递归方法实现的中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res=new ArrayList<Integer>();
        if(root==null)return res;
        inorderT(root,res);
        return res;
    }
    public void inorderT(TreeNode root,List<Integer> res) {
        if(root!=null){
           inorderT(root.left,res);
           res.add(root.val);
           inorderT(root.right,res); 
        }
    }
}

3.后序遍历

迭代方法实现的后序遍历

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        if(root == null) return new ArrayList<Integer>();
        List<Integer> result = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
        while(!stack.empty()){
            TreeNode ele = stack.pop();
            result.add(0,ele.val);
            if(ele.left != null)
                stack.push(ele.left);
            if(ele.right != null)
                stack.push(ele.right);
        }
        return result;
    }
}

递归方法实现的后续遍历

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<Integer>();
        postOrder(root,list);
        return list;
    }
    public void postOrder(TreeNode root,List<Integer> list){
        if (root != null){
            postOrder(root.left,list);
            postOrder(root.right,list);
            list.add(root.val);
        }
    }
}

4.层序遍历

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        if(root == null) return new ArrayList<List<Integer>>();
        List<List<Integer>> outside = new ArrayList<List<Integer>>();
        Queue<TreeNode> quene = new LinkedList<TreeNode>();
        quene.offer(root);
        while(quene.size() != 0){
            List<Integer> inside = new ArrayList<Integer>();
            Queue<TreeNode> quene2 = new LinkedList<TreeNode>();
            while(quene.size() != 0){
                TreeNode node = quene.poll();
                inside.add(node.val);
                if(node.left != null){
                    quene2.offer(node.left);
                }
                if(node.right != null){
                    quene2.offer(node.right);
                }
            }
            outside.add(inside);
            quene = quene2;
        }
        return outside;
    }
}