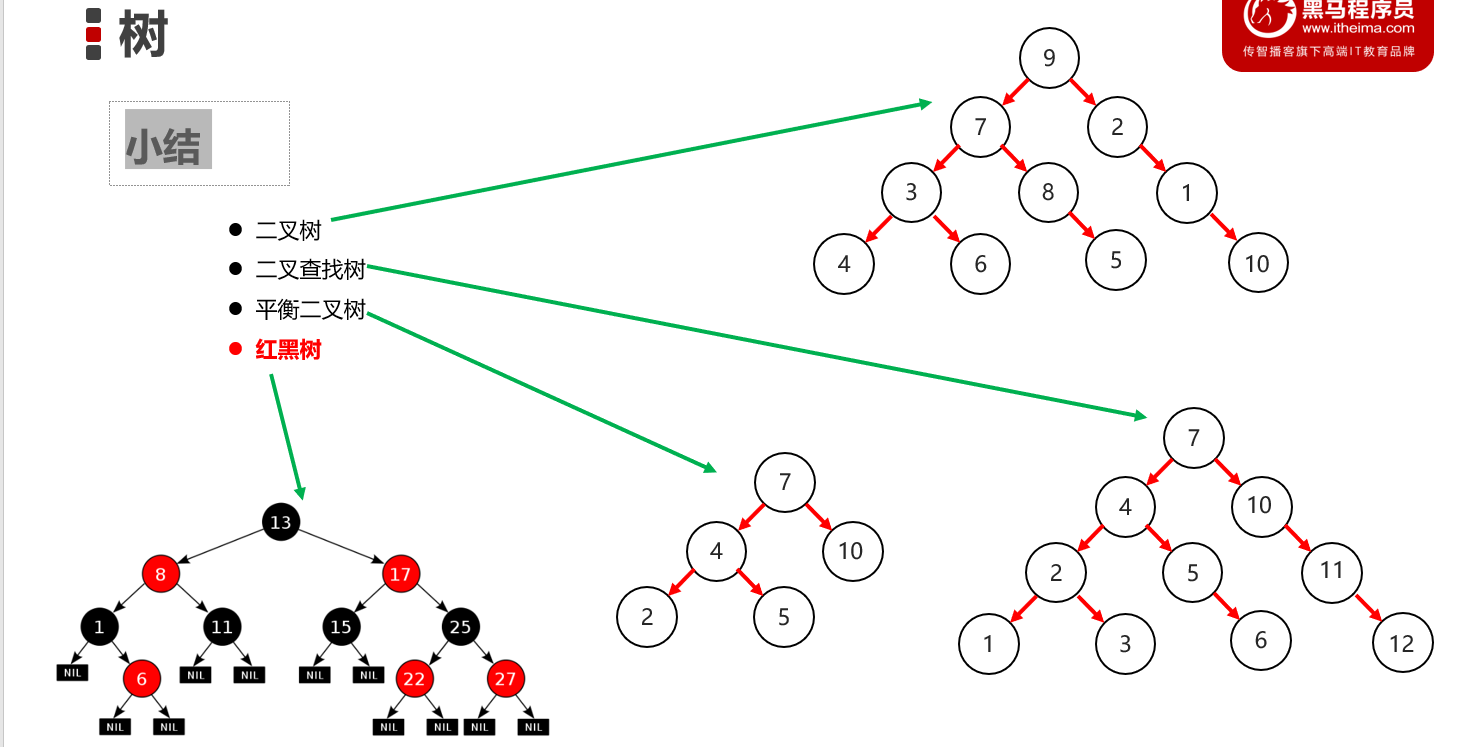
数据结构-二叉树

二叉树是指每个节点的子节点数量不超过2
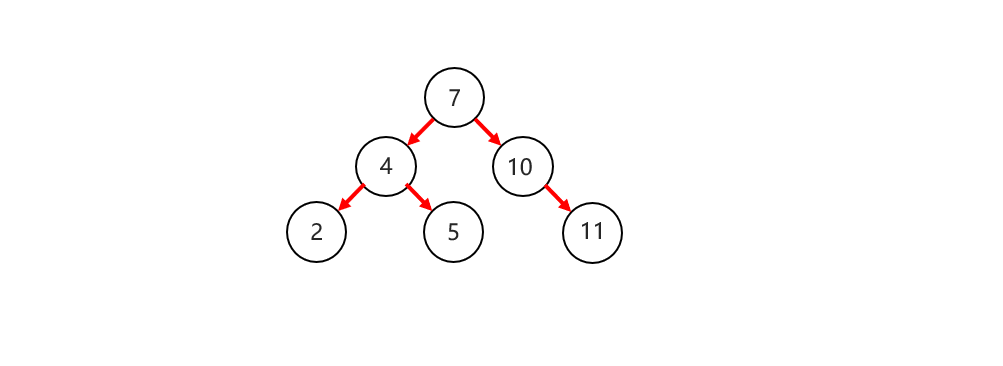
image.png

二叉查找树

在二叉树的基础上，元素排列有顺序，左子树元素小，右子树元素大。
二叉查找树相比于普通二叉树的优势在于查找速度较快。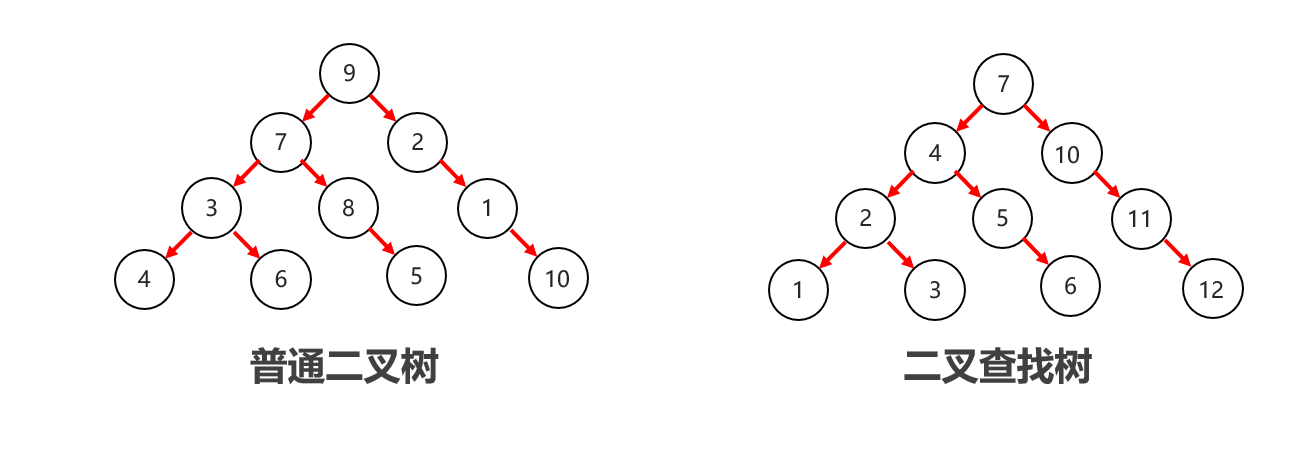
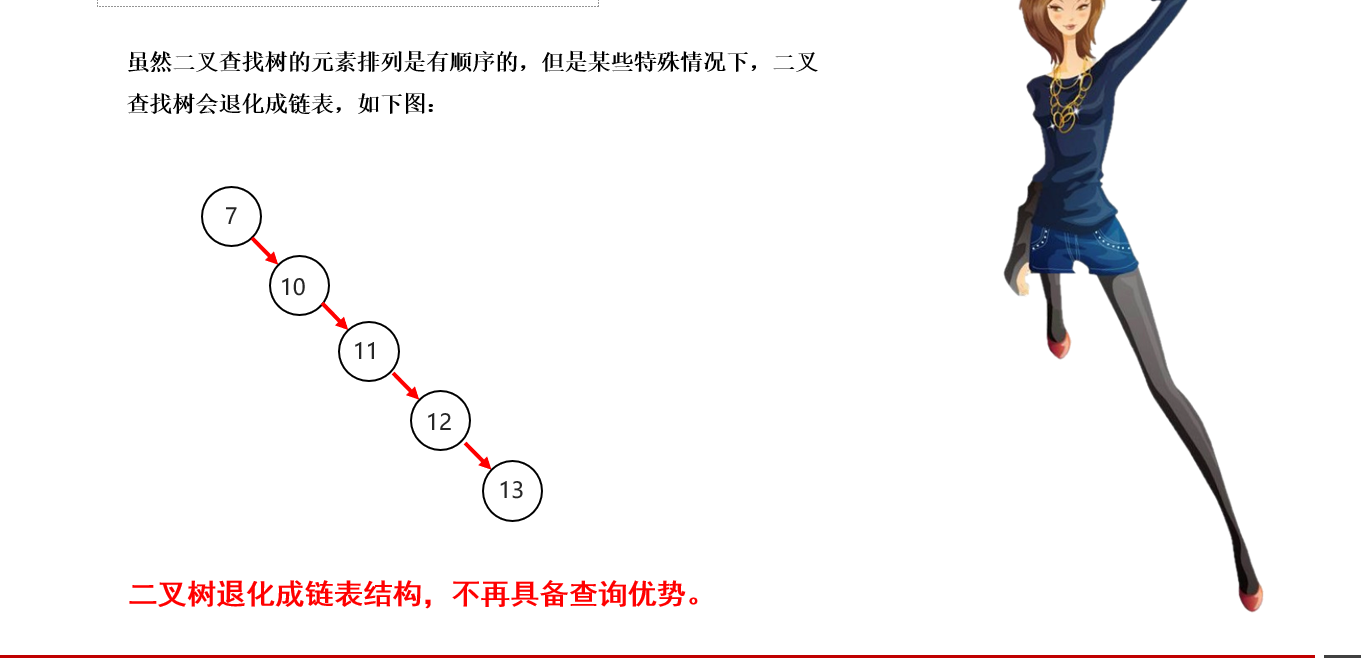
image.png

二叉查找树缺点

image.png

平衡二叉树（AVL树）

平衡二叉树左右两个子树的高度差不超过1。
任意节点的左右两个子树都是一颗平衡二叉树。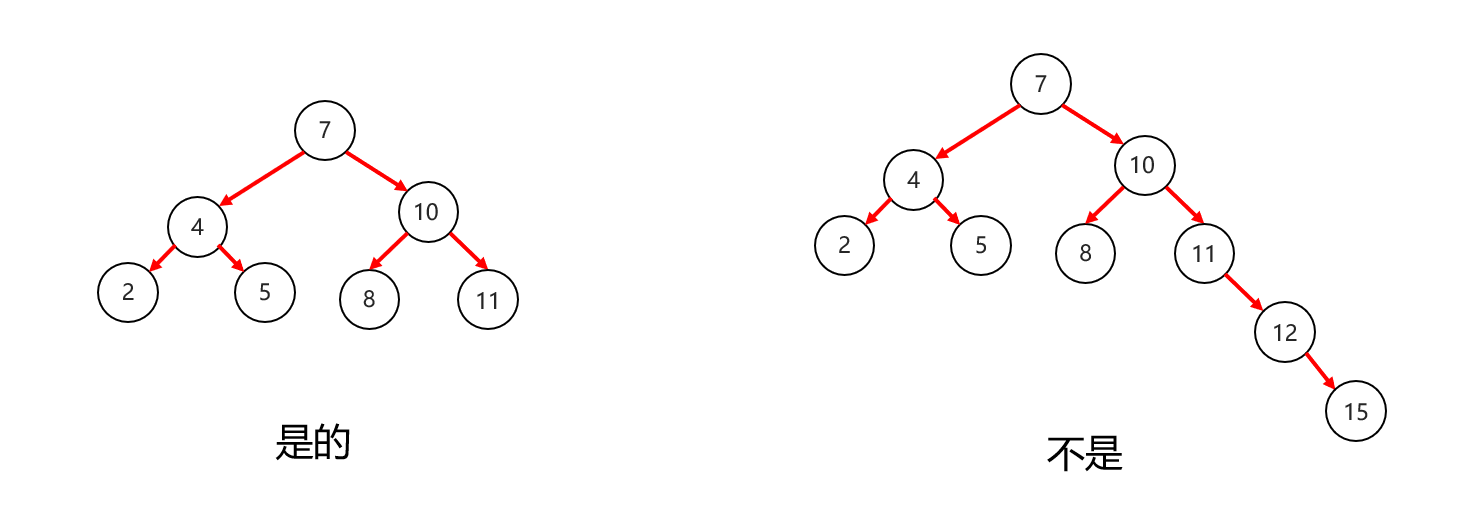
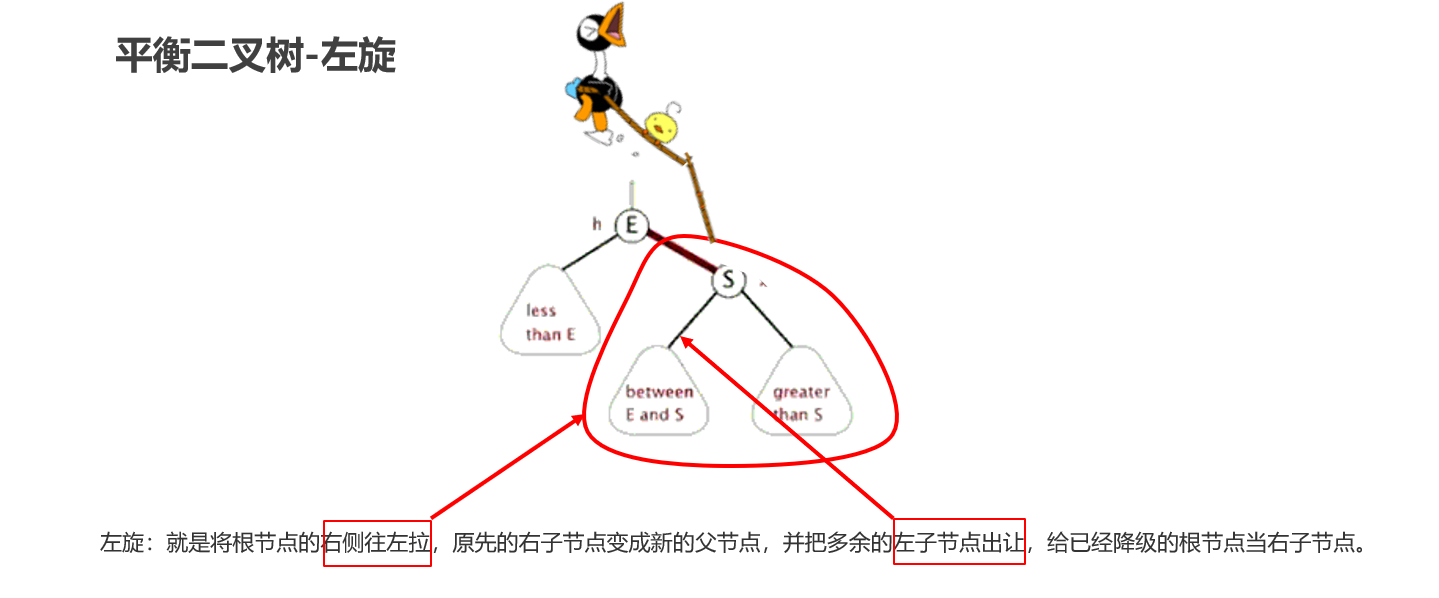
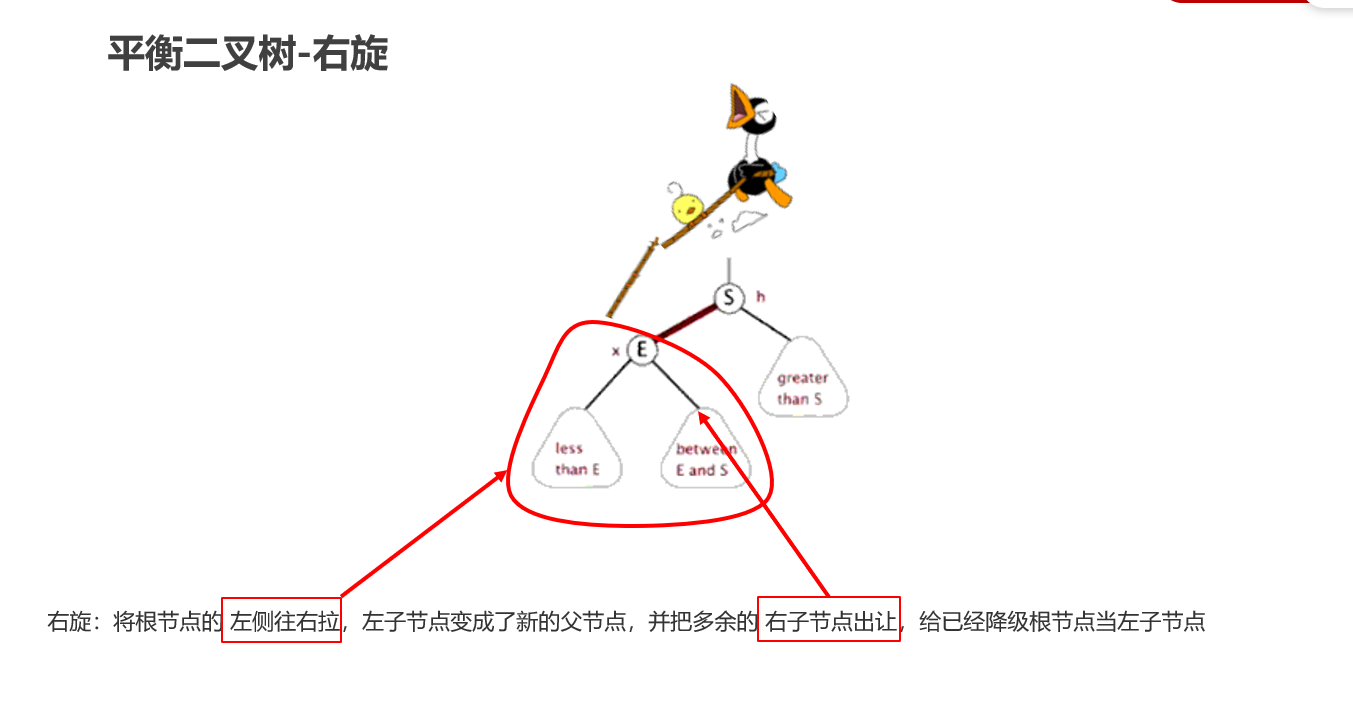
image.png

平衡二叉树-旋转

image.png
image.png
image.png

平衡二叉树小结

平衡二叉树是高度平衡的，当执行插入或者删除操作时，只要左右子树高度差超过1时，就要通过旋转来保持平衡，而旋转是非常耗时的。
由此可见，平衡二叉树适用于元素增删较少，而查找较多的场景。
由于维护高度平衡的代价较大，故而平衡二叉树实际的应用不多，更多时候会选择更加高效的红黑树。

红黑树

概述

红黑树是特殊的二叉查找树，在每个节点上有一个存储位表示节点的颜色，可以是红或黑（非红即黑）。
红黑树是一种弱平衡二叉树，相对于要求严格的平衡二叉树来说，它的旋转次数相对较少。
对于查询，插入，删除都较多的情况下，我们可以使用红黑树达到整体性能的提升。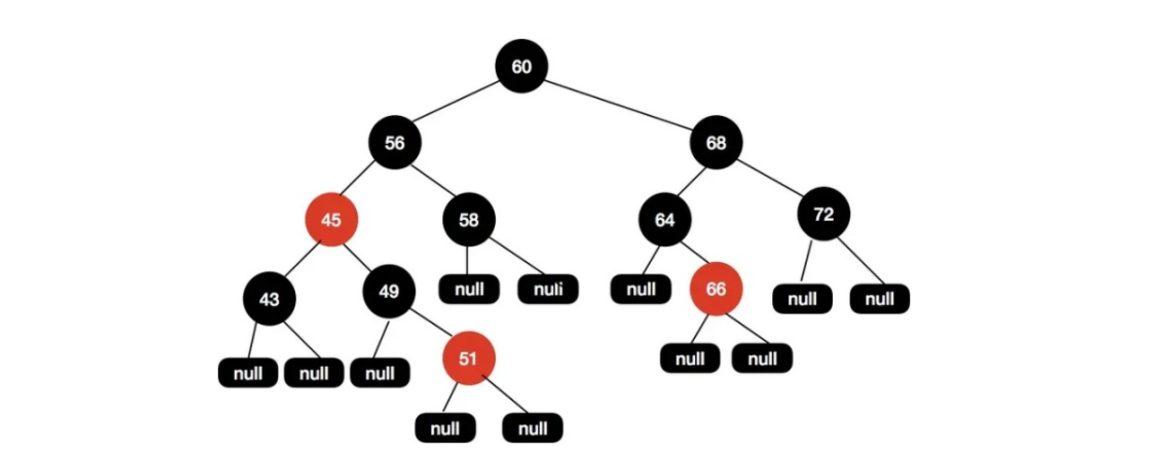
image.png

红黑树特点

红黑树不是高度平衡的，它的平衡是通过“红黑规则”进行实现的。
规则如下：
1.每一个节点或是红色的，或者是黑色的。
2.根节点必须是黑色
3.如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nil，这些Nil视为叶节点，每个叶节点(Nil)是黑色的；
4.不能出现两个红色节点相连的情况
5.对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。
6.新加入的节点是红色的，如果加入后不满足红黑规则，需要进行旋转或变色。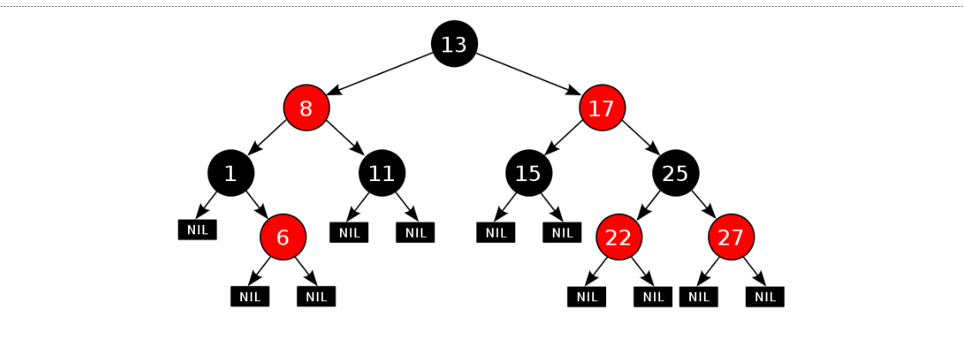image.png

小结

image.png