假设我们现在对“6 1 2 7 9 3 4 5 10 8”这10 个数进行排序。首先在这个序列中随便找一个数作为基准数。为了方便，就让第一个数6 作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在6 的右边，比基准数小的数放在6 的左边，类似下面这种排列。
3 1 2 5 4 6 9 7 10 8
方法其实很简单：分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6 的数，再从左往右找一个大于6 的数，然后交换它们。这里可以用两个变量i 和j，分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i 指向序列的最左边（即i=1），指向数字6。让哨兵j 指向序列的最右边（即j=10），指向数字8。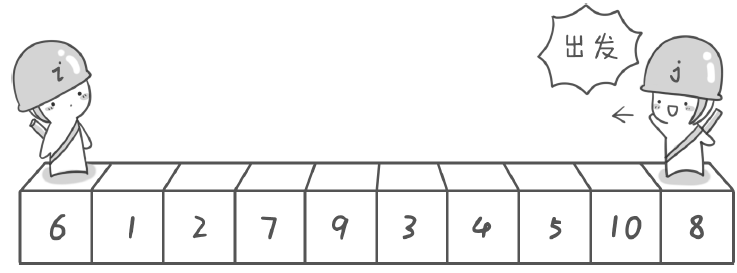

首先哨兵j 开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵j 先出动，这一点非常重要。哨兵j 一步一步地向左挪动（即j—），直到找到一个小于6 的数停下来。接下来哨兵i 再一步一步向右挪动（即i++），直到找到一个大于6的数停下来。最后哨兵j 停在了数字5 面前，哨兵i 停在了数字7 面前。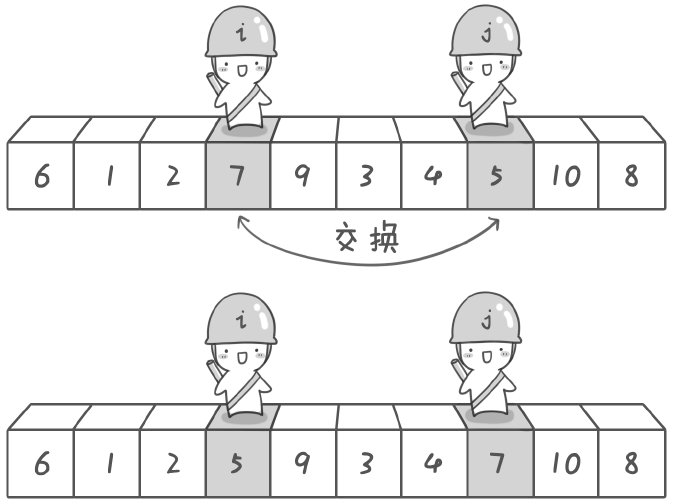

现在交换哨兵i 和哨兵j 所指向的元素的值。交换之后的序列如下。
6 1 2 5 9 3 4 7 10 8
到此，第一次交换结束。接下来哨兵j 继续向左挪动（再次友情提醒，每次必须是哨兵j 先出发）。他发现了4（比基准数6 要小，满足要求）之后停了下来。哨兵i 也继续向右挪动，他发现了9（比基准数6 要大，满足要求）之后停了下来。此时再次进行交换，交换之后的序列如下。
6 1 2 5 4 3 9 7 10 8

第二次交换结束，“探测”继续。哨兵j 继续向左挪动，他发现了3（比基准数6 要小，满足要求）之后又停了下来。哨兵i 继续向右移动，糟啦！此时哨兵i 和哨兵j 相遇了，哨兵i 和哨兵j 都走到3 面前。说明此时“探测”结束。我们将基准数6 和3 进行交换。交换之后的序列如下。
3 1 2 5 4 6 9 7 10 8

到此第一轮“探测”真正结束。此时以基准数6 为分界点，6 左边的数都小于等于6，6右边的数都大于等于6。回顾一下刚才的过程，其实哨兵j 的使命就是要找小于基准数的数，而哨兵i 的使命就是要找大于基准数的数，直到i 和j 碰头为止。
我们已经将原来的序列，以6 为分界点拆分成了两个序列，左边的序列是“3 1 2 5 4”，右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列，因为6 左边和右边的序列目前都还是很混乱的。不过不要紧，我们已经掌握了方法，接下来只要模拟刚才的方法分别处理6 左边和右边的序列即可。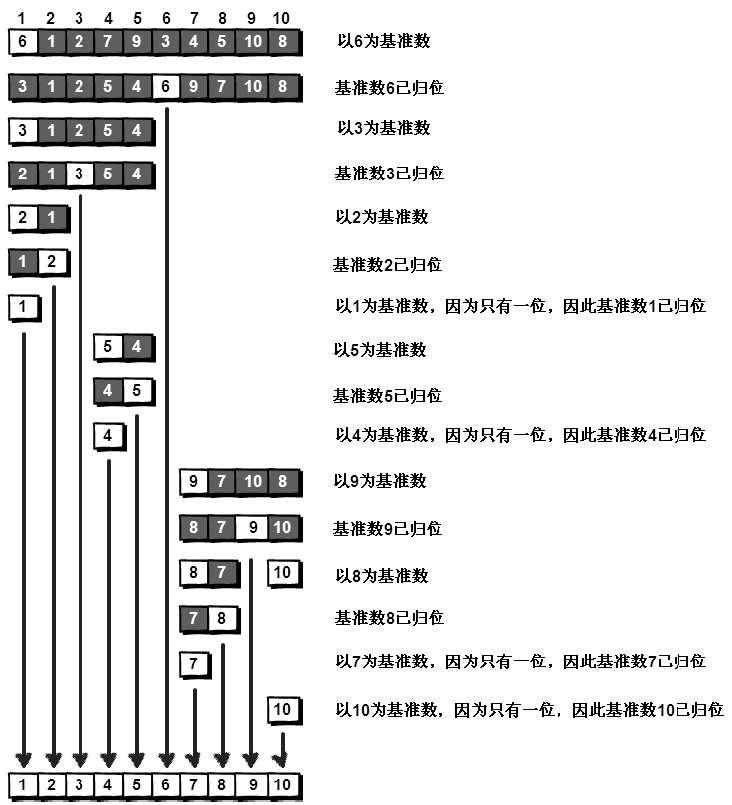

快速排序之所以比较快，是因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样只能在相邻的数之间进行交换，交换的距离就大得多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的，都是O(N^2)，它的平均时间复杂度为O (NlogN)。其实快速排序是基于一种叫做“二分”的思想。

输入输出

[Input Example]

10
6 1 2 7 9 3 4 5 10 8

[Output Example]

1 2 3 4 5 6 7 8 9 10

Solution

import java.util.Scanner;
public class quick_sort 
{
    static int N;
    static int[] a;
    public static void main(String[] args) 
    {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        a = new int[N];
        for(int i=0; i<N; i++)
            a[i] = sc.nextInt();
        sc.close();
        quicksort(0, N-1);
        for(int i=0; i<N; i++)
            System.out.print(a[i] + " ");
    }
    private static void quicksort(int left, int right) 
    {
        if(left > right)
            return;
        int temp = a[left];    //基准数
        int i = left;
        int j = right;
        while(i != j)
        {
            //从右往左找
            while(a[j]>=temp && i<j)
                j--;
            //从左往右找
            while(a[i]<=temp && i<j)
                i++;
            //i和j没有相遇时，交换两个数在数组中的位置
            if(i < j)
            {
                int t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }
        //i和j相遇了，将基准数归位
        a[left] = a[i];
        a[i] = temp;
        quicksort(left, i-1);    //递归处理基准数左边的序列
        quicksort(i+1, right);    //递归处理基准数右边的序列
    }
}