最近打算整理下树相关的数据结构，分享下，实际编程中大家应该都接触过树，举个例子，HashMap在链表尺寸大于8时升级成红黑树；Linux底层源码中大量使用了红黑树。可能掌握红黑树是一个很艰难的过程，我看了很多书，很多资料，至今没掌握红黑树，可能是资质愚钝的原因。直到去年，重新学习了下数据结构，发现其实很多事情化繁为简后，很简单，只是我们思路错了。本系列文章，我会从BST聊到BBST，后面到伸展树，再到红黑树。我们一点点把BST这个难啃的骨头，消化掉，换个角度思考问题，事情可能就会简单很多。

这是本系列的第一篇文章，我们先来聊聊BST。相信大家都接触过二分查找，查找和排序是大学算法课的基础内容。那BST和二分查找有关系吗？为什么说树是结合了Vector和List的特点的产物？相信你读完这篇文章，会有自己的答案。

BST(二叉排序树又叫二叉查找树)，英文全称是：Binary Sort Tree。网上很多资料对BST的介绍很详细，有源码，我们这里列一些不一样的东西。

特点

我们来简单过一下BST的两个特点：顺序性和单调性。

顺序性

二叉树的定义要求：

  • 任一节点均不小于其左后代
  • 任一节点均不大于其右后代
    BST - 二叉搜索树 - 图1

单调性

从顺序性我们能看出，每个BST的局部都是有序的。如果我们把每个有序的局部连起来，是不是能做到全局有序？即：BST的中序遍历（中序遍历是指以左-中-右的方式遍历）序列，必然单调非降。
这个特点也是是不是BST的充要条件。
BST - 二叉搜索树 - 图2

如上图，我们以中序遍历得到的序列是:11,12,13,15,16,18,20,25，是一个单调非降的序列。按照这个方式，BST也可以退化成一个链表。

上面的特点很简单，没看出什么亮点。既然我们都有了数组和向量，为什么还要用BST呢？我们来看一下在BST在查找、插入、删除三个
操作方面有什么特点。

查找操作

利用BST的“顺序性”，我们可以很好的检索数据。
BST - 二叉搜索树 - 图3

上图是从一个BST中查找值为8的流程。可以看到在BST树上查找的过程，本质上就是一个二分查找的过程。这个过程也是减而治之的过程：从根节点触发，逐步的缩小查找范围，直到发现目标（成功），或查找范围缩小至空树（失败）。整个耗时其实和要查找的节点的高度有关，这里我们假设目标节点的高度为h，那么查找时间为h

源码实现

  1. def search_recursively(key, node):
  2.     if node is None or node.key == key:
  3.         return node
  4.     if key < node.key:
  5.         return search_recursively(key, node.left)
  6.     if key > node.key:
  7.         return search_recursively(key, node.right)

插入操作

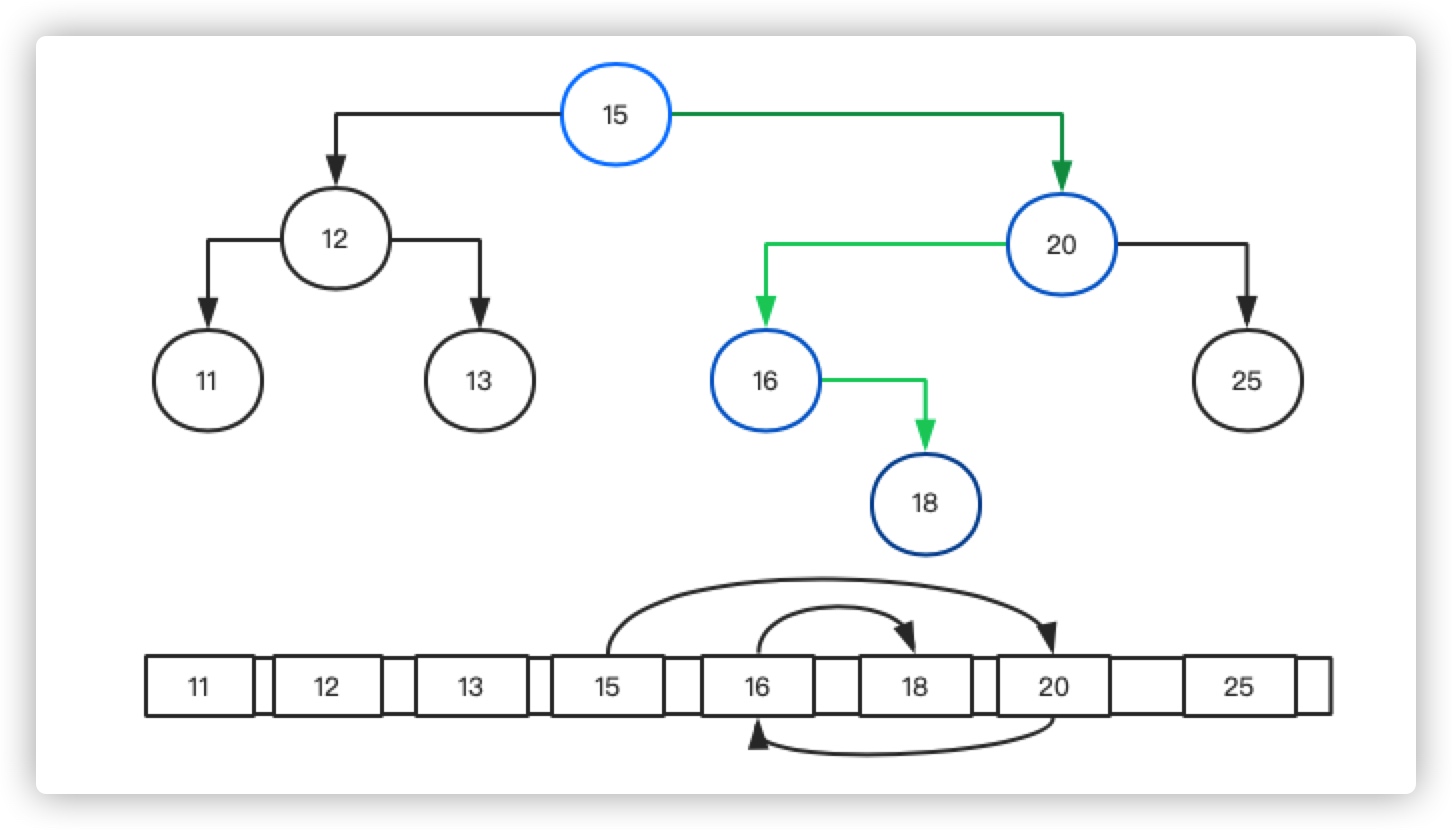
假设我在上面的例子中插入一个Key为19的数据，我们该如何操作呢？插入其实有两种情况：

  1. 树中有该Key，这种情况下，可以根据数据要求，自定义冲突规则，我们默认将Value替换。
  2. 如果树中没有该Key，这种情况下，直接插入到找到节点的左/右节点

针对情况二，我们的插入流程如下：

  1. 先查找树中有没有为19的节点
  2. 如果没有，将19写入到Guard节点，并和Parent节点关联。
    如下图所示：
    BST - 二叉搜索树 - 图4

无论是树还是数组，插入操作都要先找到目标位置，我们来看下对树和对下面数组进行插入操作的时间：

  • 在BST上进行插入操做 = 查找操作h + 1次写操作的时间
  • 但在数组上进行插入操作 = 二分查找log(n) + 1次写入 + n次移动时间，这里扩容时间忽略不计，我们假设数组是无界的。

从插入操作我们可以看出，BST本质上是结合了Vector和List的优点：

  • Vector是插入和修改比较便利
  • List是利用索引查找比较便利，这里的List只得是允许根据下标访问的数组。

源码实现

  1. def binary_tree_insert(node, key, value):
  2.     if node is None:
  3.         return NodeTree(None, key, value, None)
  4.     if key == node.key:
  5.         return NodeTree(node.left, key, value, node.right)
  6.     if key < node.key:
  7.         return NodeTree(binary_tree_insert(node.left, key, value), node.key, node.value, node.right)
  8.     return NodeTree(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))

删除操作

其实查找和插入都比较简单，复杂的是删除操作。删除操作也分两种情况：

  • 单分支：如果没有右孩子/左孩子，或者该节点没有孩子
  • 双分支：如果待删除的节点，有左子树，也有右子树

单分支

针对单分支的情况，处理起来，比较简单，如果该节点没有后代。直接删除该节点就好了。例如，我们在上面的数据中，删除18节点。
BST - 二叉搜索树 - 图5
如果当前节点只有一个后代，例如删除图中的16。只需要删除该节点，并把当前节点的一个child放到原来自己的位置就可以。如下图：
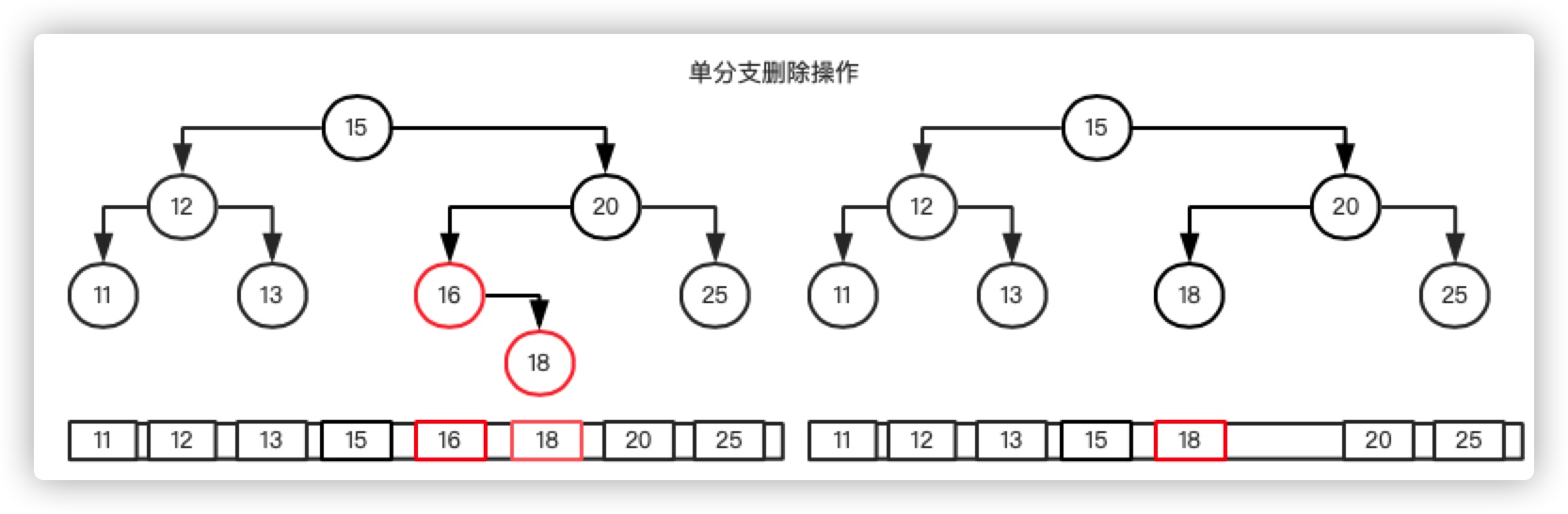
BST - 二叉搜索树 - 图6

我们来看一下算法复杂度，在树上进行单分支的删除操作，同样是一次search，一次清除。但如果是数组上进行删除，需要移动元素。

双分支

双分支的情况可能比较复杂，要考虑的因素也比较多，但我们其实可以想办法将双分支转换为单分支，来简化复杂度。同样是上面的数据，我们分析下删除节点15的流程。
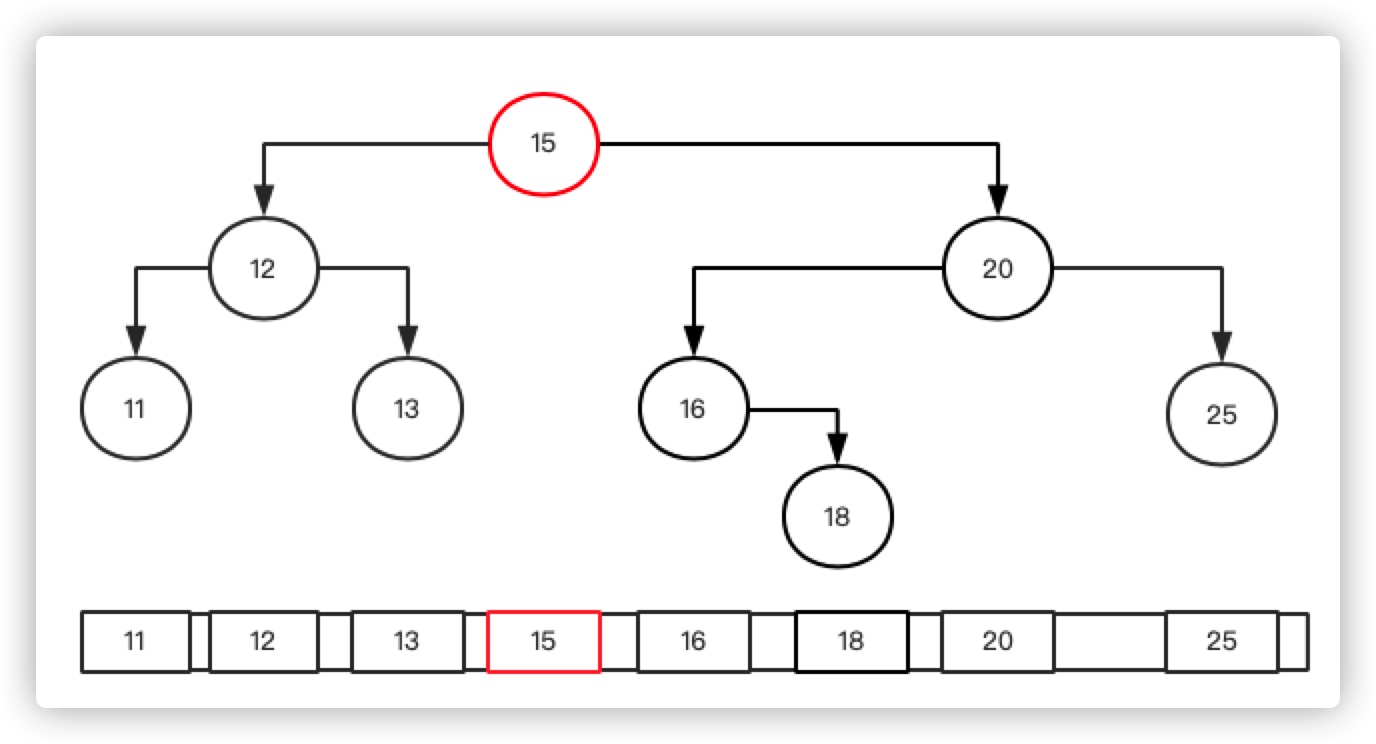
BST - 二叉搜索树 - 图7
如上图，如果我们想把节点15退化成单分支：

  • 从树的角度看那他一定要在树的最低端，变成叶节点，或者叶节点的父亲。并且不能破坏BST的顺序性。

  • 从数组角度看，如果不破坏顺序性，节点15删除后的顺序为：11，12，13，16，18，20，25。所以想把15删除，必定不能将15移动到13前面，或者16后面，他只能和13或者16互换，这样移除15后能保证顺序不变。

    • 和13互换，11，12，15，13，16，18，20，25。
    • 和16互换，11，12，13，16，15，18，20，25。

事情看起来明了了，如何在树中找到13/16节点？这里要引入新概念前驱节点和后继节点。我们看一下Wiki的解释

A node’s in-order successor is its right subtree’s left-most child, and a node’s in-order predecessor is the left subtree’s right-most child.

  • 中序遍历的前驱节点：就是当前节点的左子树中最右的节点。在我们的例子中是：13。
  • 中序遍历的后继节点：就是当前节点的右子树中最左的节点。在我们的例子中是：16。

后继节点的代码示例：

  1. def find_min(self):
  2.     """Get minimum node in a subtree."""
  3.     current_node = self
  4.     while current_node.left_child:
  5.         current_node = current_node.left_child
  6.     return current_node

我们来看一下总流程：
BST - 二叉搜索树 - 图8

源码实现

我们来看一下源码实现：

  1. def replace_node_in_parent(self, new_value=None) -> None:
  2.     if self.parent:
  3.         if self == self.parent.left_child:
  4.             self.parent.left_child = new_value
  5.         else:
  6.             self.parent.right_child = new_value
  7.     if new_value:
  8.         new_value.parent = self.parent
  10. def binary_tree_delete(self, key) -> None:
  11.     if key < self.key:
  12.         self.left_child.binary_tree_delete(key)
  13.         return
  14.     if key > self.key:
  15.         self.right_child.binary_tree_delete(key)
  16.         return
  17.     # Delete the key here
  18.     if self.left_child and self.right_child:  # If both children are present
  19.         successor = self.right_child.find_min()
  20.         self.key = successor.key
  21.         successor.binary_tree_delete(successor.key)
  22.     elif self.left_child:  # If the node has only a *left* child
  23.         self.replace_node_in_parent(self.left_child)
  24.     elif self.right_child:  # If the node has only a *right* child
  25.         self.replace_node_in_parent(self.right_child)
  26.     else:
  27.         self.replace_node_in_parent(None)  # This node has no children

思考

为什么要求所有当前节点不大于/不小于subtree，而不是child？

在将顺序性的时候，我们说根据BST定义，当前节点应不小于/不大于当前节点的左/右后代，而不是不小于/不大于当前节点的左/右孩子呢？可能是中英文差异的原因，也可能是理解的问题，所以这里我们统一一下语言：

  • subtree：子树、后代，不仅仅包含子节点，也包含子节点的子节点的子节点等。哈哈。
  • child：孩子，子节点。

其实，如果如果只是不大于/不小于子孩子会破坏全局顺序性，例如下图：
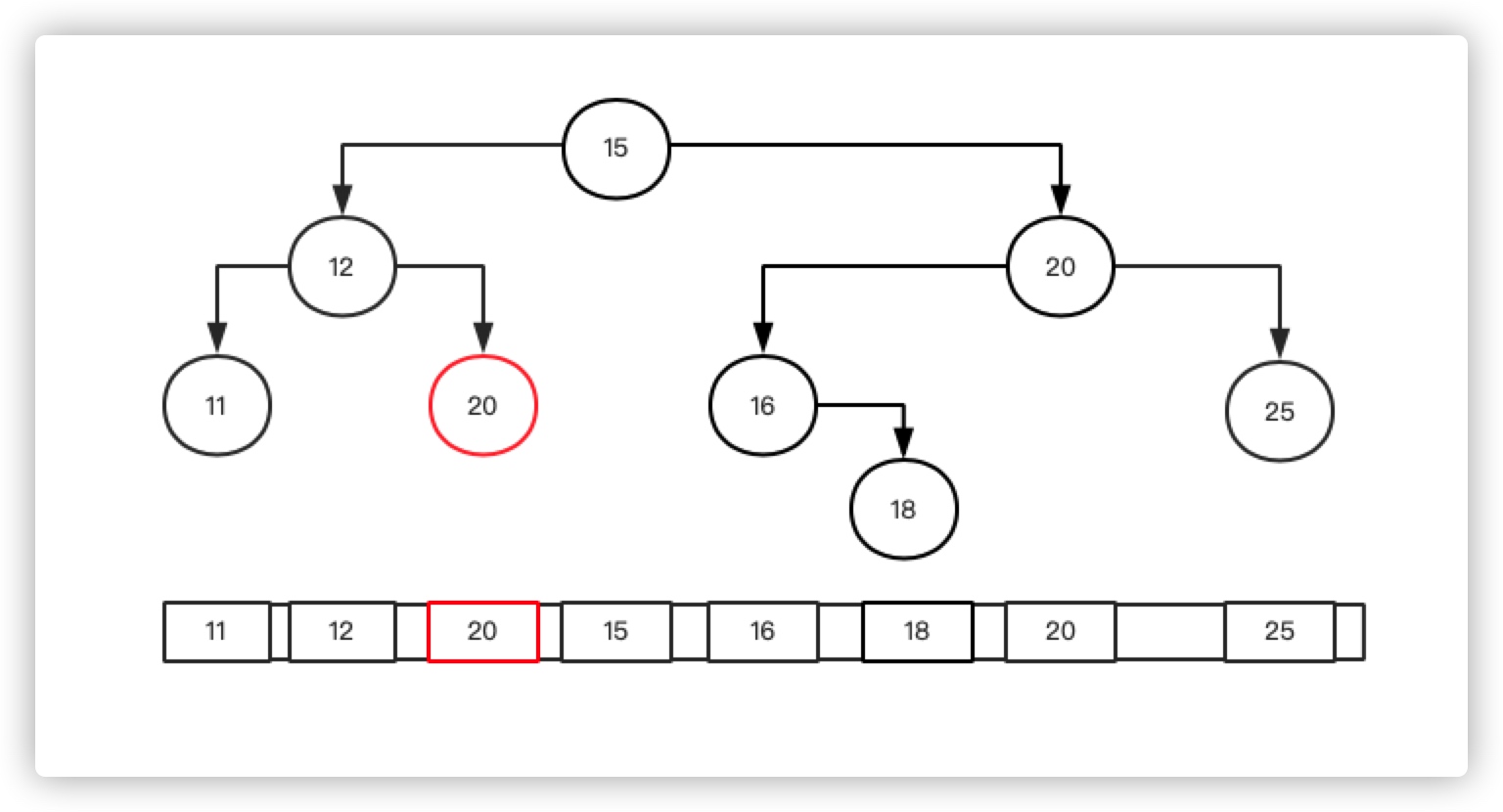
BST - 二叉搜索树 - 图9
20和15顺序是有问题的，破坏了全局单调不降。

BST稳定吗？

正如我们前面所说的：BST = Vector + List，BST充分发挥了两者的优势。但我们目前实现的这种BST还很粗糙。我们来简单分析下算法复杂度，阐明当前BST的缺点。
根据我们上面的分析，当前这棵树的所有操作的复杂度，都和h（树的高度）成正比。所以极端情况下，如果h=n（总元素数量），当前树就退化成了向量（可以理解为链表)，优势当然无存。
可以通过两种方式来分析下，n个节点的情况下，BST的平均高度：

  • 通过排列的方式。将插入的顺序理解为排列的顺序，如果只有1，2，3三个节点，那么可能的排列为6。如果有n个节点，可能的排列为n!，树的平均高度为log(n)，这个大家可以网上找一些资料来证明该结论。
  • 我们也可以按照组合的方式分析下BST的平均高度，即在不破坏顺序性的前提下，节点所能组合出的树的总数。根据分析，树的总数为catalin数，那么树的平均高度为BST - 二叉搜索树 - 图10。有关catalin数可以查阅wiki。

由于第一种方式，不同的序列可能生成重复的树，所以第二种方式的值更加精准。但BST - 二叉搜索树 - 图11可不是个好数字。

那么我们通过控制树的高度，进而让BST更加稳定呢？我们会在下篇文章中分析AVL。看一看AVL是如何控制树的高度，达到理想平衡。

重构

上面的三个操作，其实都用到了树搜索，我们可以设置将查询的过程提取一个公共函数。

参考资料

  1. WIKI-Binary Search Tree: https://en.wikipedia.org/wiki/Binary_search_tree
  2. 学堂在线 - 数据结构（邓俊辉教授）: https://next.xuetangx.com/course/THU08091002048/1515966