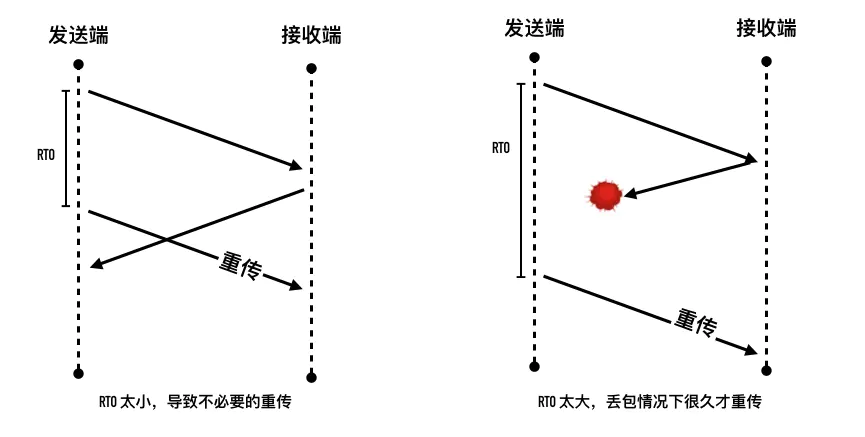
image.png

间隔多久重传就是不是一成不变的，它随着不同的网络情况需要动态的进行调整，这个值就是今天要介绍的「超时重传的时间」（Retransmission TimeOut，RTO），它与 RTT 密切相关，下面我们来介绍几种计算 RTO 的方法

经典方法（适用 RTT 波动较小的情况）

经典算法引入了「平滑往返时间」（Smoothed round trip time，SRTT）的概念：经过平滑后的RTT的值，每测量一次 RTT 就对 SRTT 作一次更新计算:

  1. SRTT = ( α * SRTT ) + ((1- α) * RTT)

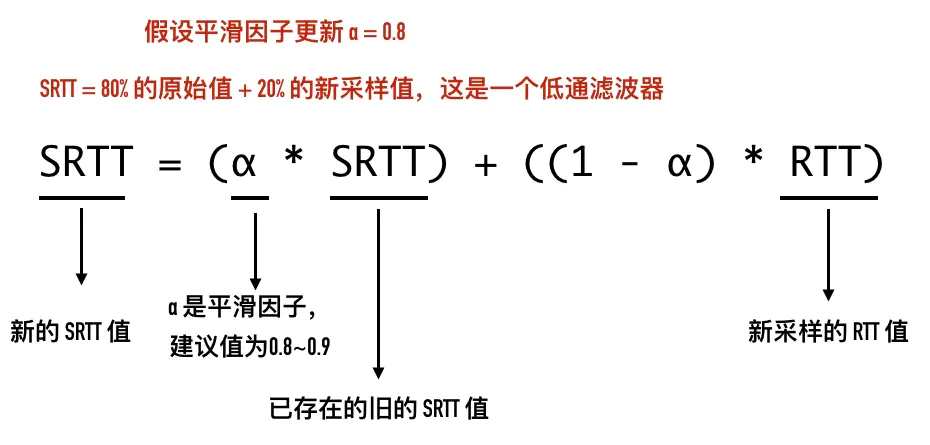
image.png

  • 当 α 趋近于 1 时，1 - α 趋近于 0，SRTT 越接近上一次的 SRTT 值，与新的 RTT 值的关系越小，表现出来就是对短暂的时延变化越不敏感。
  • 当 α 趋近于 0 时，1 - α 趋近于 1，SRTT 越接近新采样的 RTT 值，与旧的 SRTT 值关系越小，表现出来就是对时延变化更敏感，能够更快速的跟随时延的变化而变化

超时重传时间 RTO 的计算公式是：

RTO = min(ubound, max(lbound, β * SRTT))

image.png

这个算法下，平滑因子 α 取值范围是 0.8 ~ 0.9，RTT 对 RTO 的影响太小了，在相对稳定RTT 的网络环境中，这个算法表现还可以，如果在一个 RTT 变化较大的环境中，则效果较差。

标准方法（Jacobson / Karels 算法）

传统方法最大的问题是RTT 有大的波动时，很难即时反应到 RTO 上，因为都被平滑掉了。标准方法对 RTT 的采样增加了一个新的因素:

SRTT = (1 -  α) * SRTT +  α * RTT            // 预测值
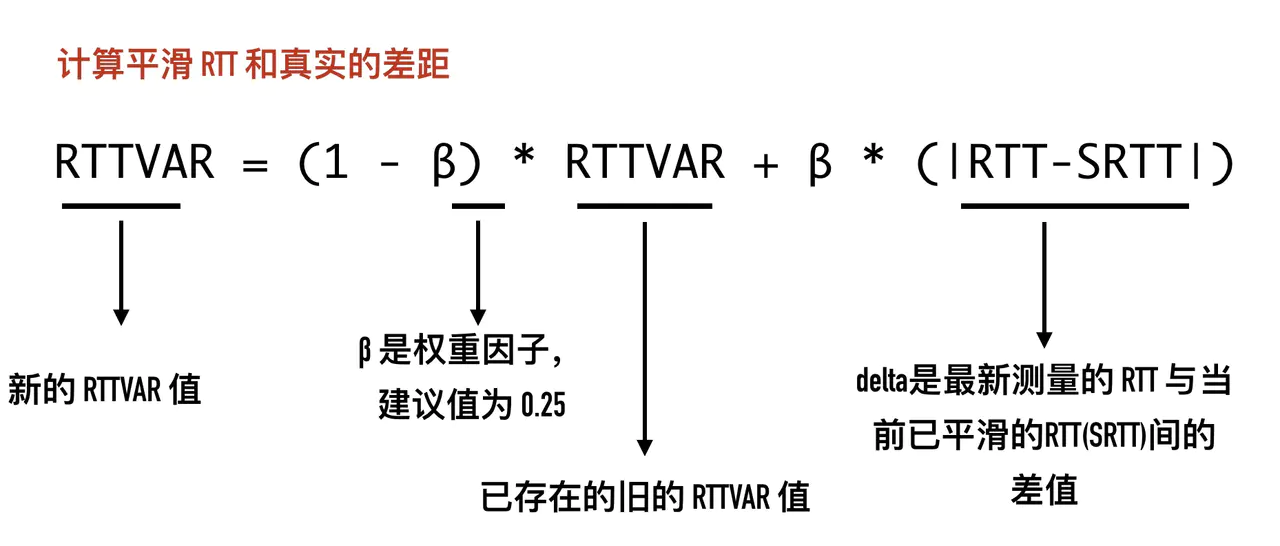
RTTVAR = (1 - β) * RTTVAR + β * (|RTT-SRTT|) // 偏差值
RTO= µ * SRTT + ∂ * RTTVar                   // 预测修正值
  1. SRTT = (1 - α) SRTT + α RTT

image.png

  1. RTTVAR = (1 - β) RTTVAR + β (|RTT-SRTT|)
    1. RTTVAR：「已平滑的 RTT 平均偏差估计器」（round-trip time variation，RTTVAR）

image.png

  1. RTO= µ SRTT + ∂ RTTVar
    1. μ 建议值取 1，∂ 建议值取 4

这种算法下 RTO 与 RTT 变化的差值关系更密切，能对变化剧烈的 RTT做出更及时的调整。

重传二义性与 Karn / Partridge 算法

前面的算法都很精妙，但是有一个最基本的问题还没解决，如何重传情况下计算 RTT，下面列举了三种常见的场景:

image.png

Karn / Partridge 算法就是为了解决重传二义性的。它的思路也是很奇特，解决问题的最好办法就是不解决它：

  • 既然不能确定 ACK 包到底对应重传包还是非重传包，那这次就忽略吧，这次重传的 RTT 不会被用来更新 SRTT 及后面的 RTO
  • 只有当收到未重传过的某个请求的 ACK 包时，才更新 SRTT 等变量并重新计算RTO

Karn 算法采用了出现重传就将 RTO 翻倍的方法，这就是我们前面看到过的指数级退避（Exponential backoff）。这种方式比较粗暴，但是非常简单。