numpy和tensorflow中的广播机制 - _harvey - 博客园

广播的引出

numpy 两个数组的相加、相减以及相乘都是对应元素之间的操作。

import numpy as np

x = np.array([[2,2,3],[1,2,3]])
y = np.array([[1,1,3],[2,2,4]])
print(x*y) #numpy 当中的数组相乘是对应元素的乘积，与线性代数当中的矩阵相乘不一样

输入结果如下：
‘‘‘
[[ 2 2 9]
[ 2 4 12]]
‘‘‘

当两个数组的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）。

比如，一个二维数组减去列平均值，来对数组的每一列进行距平化处理：

import numpy as np

arr = np.random.randn(4,3) #shape(4,3)
arr_mean = arr.mean(0) #shape(3,)
demeaned = arr -arr_mean

很明显上式 arr 和 arr_mean 维度并不形同，但是它们可以进行相减操作，这就是通过广播机制来实现的。

广播的原则

如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为 1，则认为它们是广播兼容的。广播会在缺失和（或）长度为 1 的维度上进行。

这句话乃是理解广播的核心。广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为 1。

数组维度不同，后缘维度的轴长相符

我们来看一个例子：

import numpy as np

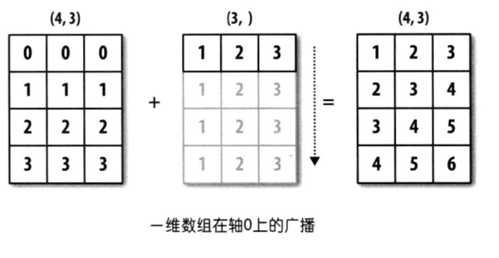
arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]]) #arr1.shape = (4,3)
arr2 = np.array([1, 2, 3]) #arr2.shape = (3,)
arr_sum = arr1 + arr2
print(arr_sum)

输入结果如下:
‘‘‘
[[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]]
‘‘‘

上例中 arr1 的 shape 为（4,3），arr2 的 shape 为（3，）。可以说前者是二维的，而后者是一维的。但是它们的后缘维度相等，arr1 的第二维长度为 3，和 arr2 的维度相同。arr1 和 arr2 的 shape 并不一样，但是它们可以执行相加操作，这就是通过广播完成的，在这个例子当中是将 arr2 沿着 0 轴进行扩展。

上面程序当中的广播如下图所示：

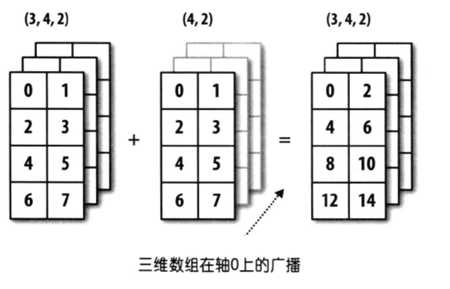
同样的例子还有：

从上面的图可以看到，（3,4,2）和（4,2）的维度是不相同的，前者为 3 维，后者为 2 维。但是它们后缘维度的轴长相同，都为（4,2），所以可以沿着 0 轴进行广播。

同样，还有一些例子：（4,2,3）和（2,3）是兼容的，（4,2,3）还和（3）是兼容的，后者需要在两个轴上面进行扩展。

数组维度相同，其中有个轴为 1

我们来看下面的例子：

import numpy as np

arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]]) #arr1.shape = (4,3)
arr2 = np.array([[1],[2],[3],[4]]) #arr2.shape = (4, 1)

arr_sum = arr1 + arr2
print(arr_sum)

输出结果如下：
[[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]

arr1 的 shape 为（4,3），arr2 的 shape 为（4,1），它们都是二维的，但是第二个数组在 1 轴上的长度为 1，所以，可以在 1 轴上面进行广播，如下图所示：

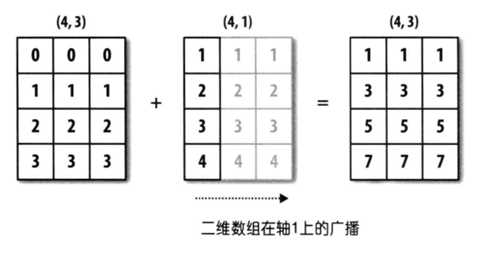
在这种情况下，两个数组的维度要保证相等，其中有一个轴的长度为 1，这样就会沿着长度为 1 的轴进行扩展。这样的例子还有：（4,6）和（1,6） 。（3,5,6）和（1,5,6）、（3,1,6）、（3,5,1），后面三个分别会沿着 0 轴，1 轴，2 轴进行广播。

后话：还有上面两种结合的情况，如（3,5,6）和（1,6）是可以相加的。在 TensorFlow 当中计算张量的时候也是用广播机制，并且和 numpy 的广播机制是一样的。
https://www.cnblogs.com/harvey888/p/10211800.html