一、排列问题

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。 示例一： 输入：nums = [1,1,2] 输出： [[1,1,2], [1,2,1], [2,1,1]] 示例二： 输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

1. 解题思路：

本题在LeetCode的46题中增加了数组中元素可重复这一条件，但要求：返回的结果又不能有重复元素。

首先看看46题的回溯树和回溯代码：
lc之回溯算法 - 图1

  1.     // 路径记录在path中，
  2.     // 结束条件：nums数组中的元素全都在list中，即两者的size一样
  3.     public void dfs(int[] nums, LinkedList<Integer> path) {
  4.         // 递归结束条件
  5.         if(nums.length == path.size()){
  6.             res.add(new LinkedList<>(path));
  7.             return;
  8.         }
  9.         // 单次递归操作 
  10.         for(int i = 0; i < nums.length; i++){
  11.             // 如果nums[i]已经在path中有了，就不能加了，因为全排列元素不能重复
  12.             if(path.contains(nums[i])){
  13.                 continue;
  14.             }
  15.             // if没执行就执行这句
  16.             path.add(nums[i]);
  17.             // 添加操作结束，进入下一层继续判断
  18.             dfs(nums, path);
  19.             // 当下一层完后，会返回到当前层，那么 path 就可能改变了，得回溯，回到当前层刚开始的模样
  20.             path.removeLast();
  21.         }
  22.     }

我们就可以 在搜索之前就对候选数组排序，一旦发现某个分支搜索下去可能搜索到重复的元素就停止搜索，这样结果集中不会包含重复列表。
假设数组为{1,1,2}，画出的回溯树如下图所示：
lc之回溯算法 - 图2
完整代码：

  1.     public void dfs(int[] nums, boolean[] used) {
  2.         // 递归出口
  3.         if(path.size() == nums.length)  {
  4.             res.add(new ArrayList(path));
  5.             return;
  6.         }
  7.         //
  8.         for(int i = 0; i < nums.length; i++) {
  9.             // 数字不能重复，使用了就跳过该数字
  10.             if(used[i] == true){
  11.                 continue;
  12.             }
  13.             // i > 0 是为了保证 nums[i - 1] 有意义
  14.             //写 used[i - 1]==false 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
  15.             if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false){
  16.                 continue;
  17.             }
  18.             // 选择
  19.             path.add(nums[i]);
  20.             used[i] = true;
  21.             // 下一层递归
  22.             dfs(nums, used);
  23.             // 回溯
  24.             path.removeLast();
  25.             used[i] = false;
  26.         }
  27.     }

二、组合问题

三、子集问题

78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）

输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

画出递归树：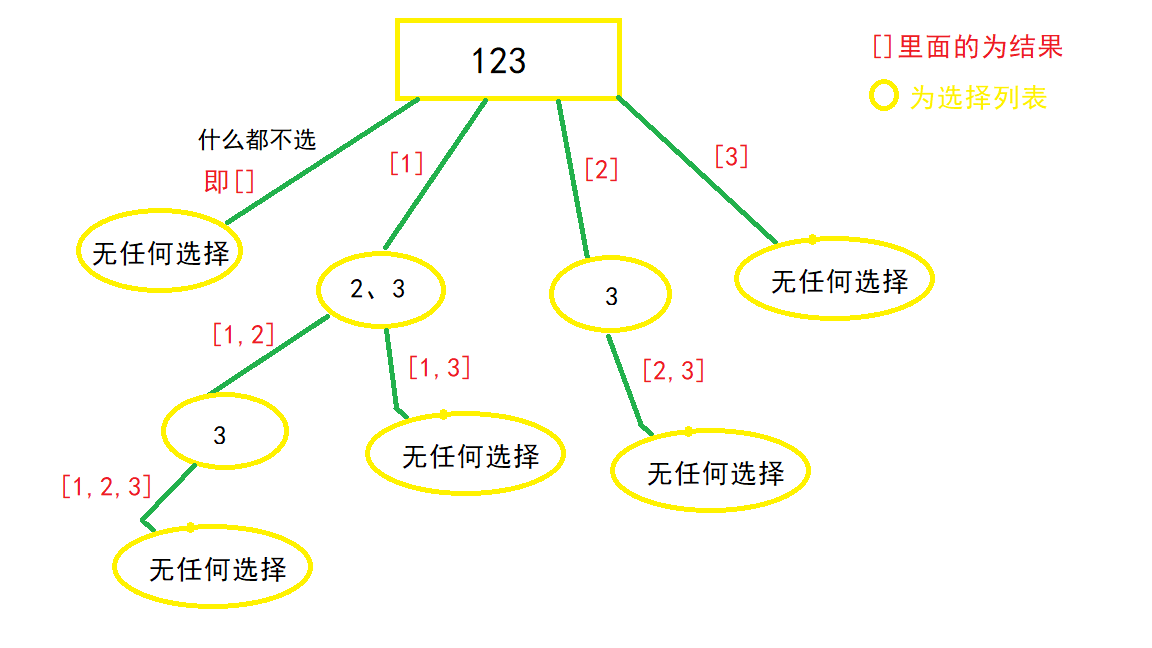
lc之回溯算法 - 图3

  • 使用一个参数start，来标识当前的选择列表的起始位置。也就是标识每一层的状态。
  • 此题非常特殊，所有路径都应该加入结果集，所以不存在结束条件。或者说当 start 参数越过数组边界的时候，程序就自己跳过下一层递归了，因此不需要手写结束条件,直接加入结果集。

  • 从递归树中看到，路径没有重复的，也没有不符合条件的，所以不需要剪枝。

    1. class Solution {
    2.   List<List<Integer>> res = new ArrayList<>();
    3.   public List<List<Integer>> subsets(int[] nums) {
    4.       if(nums == null || nums.length == 0)    return res;
    5.       List<Integer> path = new ArrayList<>();
    6.       backtrack(nums, 0, path);
    7.       return res;
    8.   }
    10.   public void backtrack(int[] nums, int start, List<Integer> path){
    11.       res.add(new ArrayList<>(path));
    13.       for(int i = start; i < nums.length; i++) {
    14.           path.add(nums[i]);
    15.           backtrack(nums, i + 1, path);
    16.           path.remove(path.size() - 1);
    17.       }
    18.   }
    19. }