从图灵到冯诺依曼
罗马不是一天建成的,计算机当然也不是。
生活中我们会将许多工具叫成“计算机”,历史上的计算机也有过数次巨大的变化发展。那么,这些机器之间有什么共性,到底什么样的机器会被叫成计算机呢?
再计算机发展史上,有两个重要的概念,分别是“图灵机”与“冯·诺依曼结构”。这两个理论是现今计算机的基石,了解他们对于编程语言的学习会很有帮助。
图灵机
简单的描述
图灵机是英国数学家艾伦·麦席森·图灵(Alan Mathison Turing,1912年6月23日-1954年6月7日)于1936年发表的论文《论可计算数在判定问题上的应用》中提出的数学模型。
简单的说,人可以解决的问题,都可以用图灵机来解决。
它可以理解成下图的样子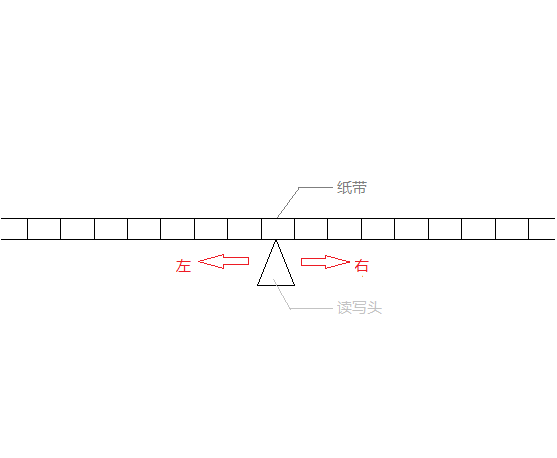
图中的纸带是一个被分成一个个小格的无限长单位,其中每个格子都可以写入或者擦除特定的信息,而负责写入或擦除信息的正是图中的读写头。
读写头可以向左或者向右移动任意个小格的距离,并根据图灵机所处的特定状态做出设定好的操作。
下面我们通过一个简单的例子来理解:
- 如果任意一个小格中是’0’,读写头到达这个小格中,设定他要给这个’0’加一。
- 如果任意一个小格中是’1’,读写头到达这个小格中,设定他把’1’变成’0’。
- 每当读写头处理完毕一个小格之后,就需要去处理下一个小格,一旦遇到’空白’小格,即停机。
现在我们构造一个简单的图灵机,用表格的方式来表示它的运行过程:
| 状态 | 小格内容 | 操作 |
|---|---|---|
| 开机 | 1 | 写入0,移到下一格 |
| 开机 | 0 | 写入1,移到下一格 |
| 停机 | 空格 | 停机 |
初始状态:
| 无限长~ | 1 | 0 | 0 | 1 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|---|
| 读写头 |
第一步:
| 无限长~ | 0 | 0 | 0 | 1 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|---|
| 读写头 |
读写头将“1”改写为“0”
第二步:
| 无限长~ | 0 | 0 | 0 | 1 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|---|
| 读写头 |
读写头右移了一位
第三步:
| 无限长~ | 0 | 1 | 0 | 1 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|---|
| 读写头 |
读写头将“0”改写为“1”
第四至第七步略……读者可以自行推导
第八步:
| 无限长~ | 0 | 1 | 1 | 0 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|---|
| 读写头 |
读写头读到空格,机器进入停机状态。
或许读者会认为,上述这样麻烦的步进过程,如果是人工来计算的话,只需要几秒钟就可以完成,完全没必要进行这样繁琐的操作。
确实,人脑思考过程的灵活性远超这样顽固的过程,而且上面的步骤也完全是在人脑中模拟进行的。我们完全没必要用人脑来进行这样耗时且繁琐的思考。
为了让读者更容易理解图灵机的意义,我们接着会进行一些更复杂的思考,并试着从人脑和图灵机的角度分别描述他们。
用图灵机实现乘法
一位数的加法运算
图灵机实际上是模仿人类计算的过程而提出的。现在想象我们在进行一个简单的一位数加法计算,例如:
如今当我们阅读“1+2”这样的算式时,会习惯性从右往左,首先得到“1”然后是“+”最后是“2”,于是我们接受的教育会告诉我们,要进行一个抽象的数学计算,用语言来表达,这个计算叫“加法”,而这个计算实际上是将它左右两边的数字,进行一个特殊的难以描述的过程(实际上在数学上有相当严格的定义)。
- 我们读到“1”并将它存在脑海中;
- 我们读到“+”并进入“计算加法”的状态;
- 我们读到“2”,于是开始计算加法,将这个“2”与存在脑海中的“1”进行一个加法运算;
- 运算结束。
总之,我们会将“1”和“2”塞进这样一个“加法”的操作里,然后得到一个新的数字“3”。
那么我们是如何知道这个加法的结果的?许多人实际上是记忆下来的,即通过类似下面表格这样的记忆,通过表中两个数相交处就是加法的结果。(部分重复的组合省略)。特别地,零加任何一个数等于这个数。
| + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | ||||||||
| 2 | 3 | 4 | |||||||
| 3 | 4 | 5 | 6 | ||||||
| 4 | 5 | 6 | 7 | 8 | |||||
| 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
接下来从图灵机的视角来看
现在我们构造一个专门用于这个加法的图灵机,它的初始状态是这样的:
| 无限长~ | 1 | + | 2 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|
| 读写头 |
首先,读写头会读取到“1”,然后读取到“+”,于是读写头进入了一个特殊的状态,这个状态会进行一个特殊的状态,这个状态会在读取到写着“+”的格子时进入,并通过这个格子两边格子的内容进行“加法”运算,然后写到后面的空格里去。
我们让它写到“2”所在的格子后面第二个空格里。
- 读取到“1”,并右移四格,然后在这个格子里写入“1”,然后左移回三格;
- 读取到“+”,进入“加法”状态,并右移一格;
- 读取到“2”,然后右移两格,然后读取里面已经写入的“1”,接着与刚刚读取到的“2”进行“加法”运算,从而将得到得结果“3”写入这个格子并覆盖掉原来的“1”;
- 停机。
终于,这个笨拙的图灵机完成了这个加法运算!
我们可以认为这个机器储存了一个和大脑一样的加法表格,当进行加法运算时可以通过两个读取到的数得出对照的结果。
如果读者仔细对比,或许会发现,图灵机的运算过程实际上和人脑的运算过程有那么些相似。
实际上,图灵的基本思想就是用机器来模拟人们用纸笔进行数学运算的过程。现在我们再更进一步试着来模拟更复杂的过程。
一位数的乘法运算
小学算术告诉我们,乘法实际上是特殊形式加法的简写。例如:
实际上是:
于是我们可以利用两个数的加法来完成这个问题,即先计算第一个加法,再将第一个加法的结果与第三个加数相加。
当然我们也可以让图灵机可以直接进入一个“乘法状态”,然后解决这个问题,毕竟我们脑海中也有乘法表。
但我们还能用另一种方式——给图灵机添加一个“循环”状态。
| 无限长~ | 9 | * | 5 | 空格 | 空格 | 空格 | 无限长~ |
|---|---|---|---|---|---|---|---|
| 读写头 |
- 读取到“9”,右移一格;
- 读取到“*”;
- 右移一格,读取到“5”,右移两格,写入“5”;
- 右移一格写入“0”,左移一格;
- 进入循环状态;
- 读取到“5”,将“5”减一并写入覆盖,左移四格读取到“9”
- 右移五格,读取到“0”,将其与刚读取到的“9”进行加法运算,将结果写入并覆盖原来的数;
- 循环上述步骤3、4,直到步骤3读取到“0”则退出循环。(注意,步骤3、4中的数字会改变)
- 关机。
多位数的加法和乘法运算
在多位数的算术运算中,我们会遇到一个新的重要问题,即参与运算的数字有无限种可能性了。
两个在一位数的加法中,参与运算的只可能是0-9这十个数字,只会出现这几个数字与其他九个数字或者与自身进行的运算。
而在更多位数的加法中,参与运算的可能是1可能是12可能是132,甚至可能是一个上亿或者更大的数字。这样我们就有了无限种可能的组合,以及他们带来的无限种结果。
不过在很久以前,这个问题就已经被前人用简化的思路解决了。
有一个调侃数学家的笑话:
一天,数学家觉得自己已受够了数学,于是他跑到消防队去宣布他想当消防员。消防队长说:“您看上去不错,可是我得先给您一个测试。”消防队长带数学家到消防队后院小巷,巷子里有一个货栈,一只消防栓和一卷软管。消防队长问:“假设货栈起火,您怎么办?”数学家回答:“我把消防栓接到软管上,打开水龙,把火浇灭。”消防队长说:“完全正确!最后一个问题:假设您走进小巷,而货栈没有起火,您怎么办?”数学家疑惑地思索了半天,终于答道:“我就把货栈点着。”消防队长大叫起来:“什么?太可怕了!您为什么要把货栈点着?”数学家回答:“这样我就把问题化简为一个我已经解决过的问题了。”
来源未知
也就是说,虽然我们无法解决所有问题,但是我们可以把未知的问题转换成已解决的问题。多位数的运算暂时留给读者自行思考,后续版本或许会增加相关内容。
上面简略地描述了图灵机的构造,要注意上面所说的纸带读写头这些东西,并不是必须的,他们只是为了方便讲述而使用的概念。实际中我们也并不存在一条无限长的纸带,所以图灵机只能停留在想象中。
而且上述内容实际上有很多内容上的省略,例如“开机”、“停机”、“加法”这样的状态如何在图灵机中保存的。如果想要更深入的了解图灵机,读者可以去搜索相关内容。
通用图灵机
现在我们可以试着用大脑构建一台简单图灵机,但是这样需要使用大脑进行复杂且繁琐的推导
那么,我们能不能设计出一种特殊图灵机,这台特殊图灵机可以去模拟任何图灵机?
答案是可以。
由此,我们就可以用这台特殊图灵机去解决所有计算问题,这种特殊图灵机被称为“通用图灵机”。
冯·诺依曼结构
图灵机只是一个理想的设备,笼统的说,它可以解决任何人可以解决得数学问题(不论代价)。所以,如果一个计算机系统可以模拟出通用图灵机时,我们就称它是图灵完备的;当一个图灵完备的系统可以被图灵机模拟时,我们称其是图灵等效的。也就是说,这个系统如同通用图灵机一样,理论上可以解决所有的数学问题。
那么,怎样实际制作这样一个系统呢?
冯·诺依曼结构就是一种实现通用图灵机的计算设备。现如今,绝大部分计算机都是在冯诺依曼结构的基础上设计的。
出于篇幅考虑,具体的冯诺依曼结构将在更后面的章节详细描述。
“海日生残夜,江春入旧年。”
【未完待续】

