Segment Tree

Cosider using other algorithms before using it.
A solution for leetcode 699: Falling Squares

  1. class SegTree:
  3.     def __init__(self, nums: List[int]): 
  4.         # init the tree with intervals, nums can be sorted endpoints of them
  5.         k = len(nums)
  6.         if k <= 1:
  7.             self.n = 0
  8.             return
  9.         k -= 1
  10.         self.n = n = int(math.pow(2,int(math.ceil(math.log(k,2)))))
  12.         self.data = data = [[0,0,0,0] for i in range(2*n)] # [left, right, data1, data2]
  13.         data[n:n+k] = [[nums[i],nums[i+1],0,0] for i in range(k)]  # intervals of the leaves
  14.         for i in range(n-1,0,-1):   
  15.             data[i][1] = max(data[2*i][1], data[2*i+1][1])
  16.             data[i][0] = data[2*i][0]
  18.     def update(self, i: int, j: int, val: int, start: int=1) -> None:
  19.         # there can be two cases: 
  20.         # 1. update a node, then update bottom up (starting from one of the leaves)
  21.         # 2. update an interval, then update top down (starting from the root)
  22.         if start >= 2* self.n:
  23.             return
  24.         l,r = self.data[start][:2]
  25.         if j <= l or i >= r:
  26.             return
  27.         self.data[start][2] = max(val, self.data[start][2])  # max height
  28.         if i <=l and j >= r:
  29.             self.data[start][3] = max(val, self.data[start][3])  # min height
  30.             return
  31.         if start >= self.n:
  32.             return
  33.         self.update(i, j, val, 2 * start)
  34.         self.update(i, j, val, 2 * start + 1)
  36.     def query(self, i: int, j: int, begin:int = 1) -> int:
  37.         # there can be two cases:
  38.         # 1. query one interval
  39.         # 2. query one point
  40.         if begin >= 2* self.n:
  41.             return 0
  42.         l,r = self.data[begin][:2]
  43.         if j <= l or i >= r:
  44.             return 0
  45.         if i <= l and j >= r:
  46.             return self.data[begin][2]
  47.         return max(self.data[begin][3], self.query(i,j,2*begin),self.query(i,j,2*begin+1))

Fenwick Tree

It is also called Binary Indexed Tree (树状数组)
The problem can be soved by this often can be solved by segment tree.

Implementation

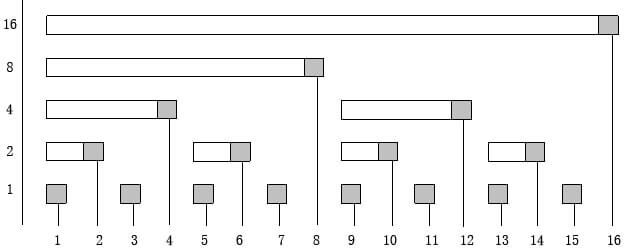
image.png
n的二进制最后一个1对应的值为： lowbit(n) = n&(-n)

注意起始从1开始，不是从0开始

  1. class FenwickTree:
  2.     def __init__(self, n):
  3.         self.sum_array = [0] * (n + 1)
  4.         self.n = n
  6.     def lowbit(self, x):
  7.         return x & -x
  9.     def add(self, x, val):
  10.         while x <= self.n:
  11.             self.sum_array[x] += val
  12.             x += self.lowbit(x)
  14.     def sum(self, x):
  15.         res = 0
  16.         while x > 0:
  17.             res += self.sum_array[x]
  18.             x -= self.lowbit(x)
  19.         return res

Problems

Leetcode 493: 链接
Leetcode 315: Count of Smaller Numbers After Self
Leetcode 327: count of range sum

Prefix Tree