想学理论的同学请移步Bilibili白板推导机器学习https://www.bilibili.com/video/BV1Hs411w7ci?spm_id_from=333.337.search-card.all.click
科研工具分享(由研二某大佬创建,欢迎提PR,issue):https://github.com/Les1ie/Awesome-research-tools
Notes
(1)二分类:就是给的一坨数据有两种类别啦,比如有一堆大佬和菜鸡写的文章,拿出一篇文章来判断它是到底是大佬还是菜鸡写的,如果你看完本文章之后判断出我是菜鸡,那么恭喜,你是一个好的分类器。
(2)线性可分:字面意思,对于二维平面上的两类数据样本点,可以通过一条直线分开,对于三维空间数据点,可以通过一个平面分开,
(3)超平面:有的时候我们的数据点不仅仅有一个,两个或者三个维度特征,有可能有三个以上的维度特征,那么我们可以统称直线、平面、高维平面啥的为超平面。每个样本点都有
个维度特征的话就是
,向量化之后就是
。这其实就是点法式啦,请你不要试图寻找
在哪里,因为,假设一个二维坐标,那么横纵坐标分别表示
.
(4)数据样式:数据样本的话基本上就是特征点和标签的样式,即,
出来喽,它指样本的标签,对于二分类就是
.
(5)对偶问题:svm涉及到对偶问题,有对偶问题必然存在原问题。原问题的对偶问题可以简单理解为从另一个角度去求解原问题,最终是等价的。比如你想毕业以后进BAT,你可以每天刷题,写代码提高工程能力,最终进BAT;也可以每天搞科研,发一堆论文,最终进BAT,反正我是进不了,你们加油。
SVM略讲
SVM无论之前还是现在都是非常受欢迎的机器学习算法,那你可能会问现在不都用深度学习嘛,额,等你参加过几次面试之后,当面试官随意的说一句“你聊一聊SVM吧”,你就知道它为啥现在还受欢迎了(不是)。<br /> 言归正传,对于一个**二分类**问题,假设它是**线性可分**的,那么我们希望能够得到一个超平面可以将这两类数据样本分开,那么这样的超平面**可能有很多个**,我们希望找到那个**最优的超平面**,即正样本(+1)在超平面上方,负样本(-1)在超平面下方,**并且正负样本离超平面尽可能的远**,防止出现分类模棱两可的问题,这个超平面有参数确定。假设超平面能够进行正确分类,对于样本集中的数据点满足下面不等式:<br /><br />我们边缘的样本点使得上述不等式的等号成立,即,这两个超平面被称为为**支持向量**,这两个不等式合起来其实是(细品)。那么我们可以通过**最大化这两个超平面到我们所求的超平面之间的距离来优化参数**,其距离之和可以表示为(平行平面之间的距离,小学二年级学过嗷),最大化这个距离就是最小化,这显然是个凸优化问题,而且要满足限制条件。(下图很形象)<br />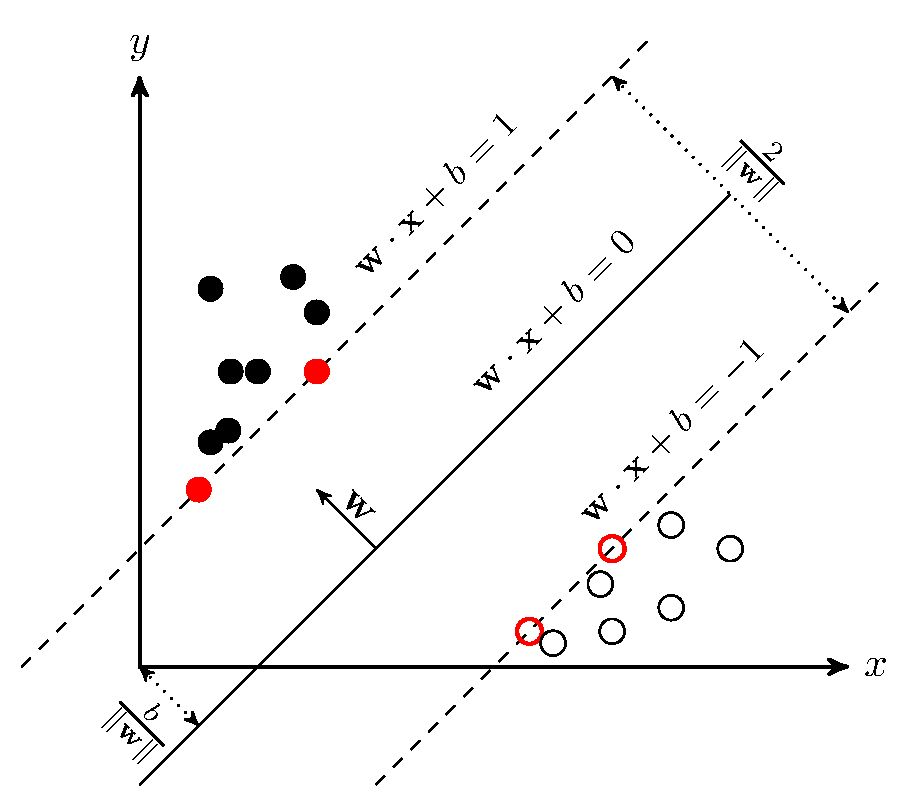<br /> 这个优化问题可以通过构建**拉格朗日乘子法**(拉格朗日乘子法求解带限制条件的函数的最优解,小学二年级学过嗷)进行求解,从而将原问题转化为其**对偶问题,如下公式,最终得到最大间隔划分超平面所对应的模型**。需要优化的参数就是和乘子参数,我们输入的样本有多少个,就有多少个。<br /><br />然后就是经典的拉格朗日乘子法步骤啦,对和求导等于0得到,,然后将这个两个式子带到上面公式就能消掉,会变成它的对偶求解公式:<br />。(这里的公式是需要推导的,感兴趣的可以推推看。另外这里是,经典的最小最大化套娃,对于最大化,这一项显然是小于等于0的,那么这项最大值是啥,那肯定是0咯,那么,套娃成功。由此也引出使用拉格朗日乘子法所需满足的KKT条件:。)<br />因此我们要去求解这一堆,它其实是一个二次规划问题,但是参数量等于样本量,直接求解开销巨大。优于限制条件,因此可以可以使用**SMO算法**。其大致思想是,每次求一对,固定其他的不变,以此求解完所有的参数,直到参数收敛。解出后,求出,最终我们求得模型:<br />.。(至于这个怎么求,可以把所有样本点带进去求得b取均值啦。)
对于线性不可分的情况,我们可以通过将样本映射到高维空间使得其在高维空间可分,假设升维函数为,即超平面为
,我们在用拉格朗日乘子法优化时,需要计算
,计算这样的高维内积是复杂的,因此我们将其转换为它们在低维的计算,引入一个核函数来表示其内积,即
。常用的核函数有线性核,多项式核,高斯核,sigmoid核,拉普拉斯核等等。
有时候,我们可能找不到这样一个超平面,或者说我们不知道找到的这个超平面是不是优于过拟合引起的。我们称必须要满足条件为硬间隔,而如果我们可以容忍间隔之间存在一些样本,给它一个容忍参数,这种方式为软间隔:
,对于函数
是一个离散函数,即不满足限制条件时为1,满足时为0,C为容忍系数。当C为无穷大时,我们要求强制满足限制条件。
SVM可以用于做回归问题,即转化为SVR,SVR和线性回归有所不同,线性回归是当点不在回归线上时就计算损失,而SVR允许一定的误差,设其为,当样本点落在
和
之间就不计算损失。因此SVR的优化目标和SVM一样,只是目的是为了容下更多的点。
在SVM中感悟生活
SVM比较重要的几个地方就是:限制条件求最优,对偶问题,SMO,核函数,软间隔。
我们可以对应这几个地方发表一些生活感悟嗷:
- 很喜欢罗翔说的一句话,人是具有社会属性的,不可能存在跟别人利益绝对无关的个人性,蝴蝶震动翅膀都有可能影响整个世界的气候,更何况是人的行为呢,你要承担因为追求自由而造成的后果,也要接受别人不喜欢你的自由。
- 换一种角度看问题,或许能得到更好地求解方式。
- 当你有很多想法要去实现而不知所措的时候,不妨每次实现其中一两个,慢慢的时间久了,或许所有的想法都能完成。
- 当生活遇到瓶颈走不出去的时候,不妨想一想初心,清楚自己真正想要的是什么,或许就能释然了。
- 不要对自己要求太严格,或许可以容忍自己犯一两次错误,在心情轻松的同时也能收获好的结果。
有啥理论或者感悟上的意见,大家可以在评论区提嗷,我读书少,欢迎批评指正!

