两样本t检验

两样本t检验用于检验两个总体的均值是否相等。两总体都是未知的，且我们不想或不易测量出总体中所有的个体，来求得总体均值进行比较。所以我们从总体中随机抽样得到样本。对两样本进行统计检验，来看两样本是否存统计学差异。

案例

  1. 若我们想知道两个不同物种的乌龟的平均重量是否相等。我们可以进行随机抽样选择部分乌龟来代表总体乌龟。由于存在误差，两个物种样本的平均重量是存在差异的。而我们可以通过two sample t-test知道它们之间的差异是否显著。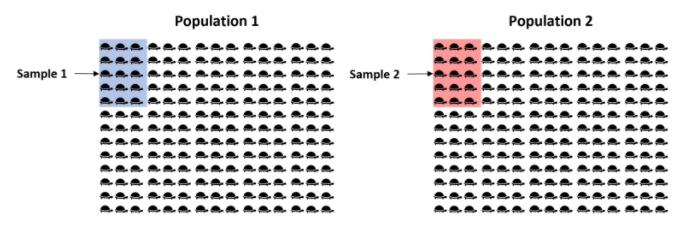
    Two Sample t-test - 图1

前提假设

为使two sample t-test结果有效，需要满足一些条件。

  1. 两总体相互独立
  2. 两总体均服从正太分布，且两总体方差相等
    • 样本应是从总体随机抽样而来

假设检验步骤

  1. 确定零假设：
    • Two Sample t-test - 图2, 假设两总体均值相等
  2. 确定备择假设，这里有3种假设方法，根据实际问题进行假设：
    • Two Sample t-test - 图3, 双侧检验，两总体均值不相等
    • Two Sample t-test - 图4, 单侧检验，总体均值Two Sample t-test - 图5小于Two Sample t-test - 图6
    • Two Sample t-test - 图7, 单侧检验，总体均值Two Sample t-test - 图8大于Two Sample t-test - 图9
  3. 计算检验统计量Two Sample t-test - 图10:
    Two Sample t-test - 图11

其中：

  • Two Sample t-test - 图12: 样本均数
  • Two Sample t-test - 图13:样本大小
  • Two Sample t-test - 图14：合并标准差
    • Two Sample t-test - 图15
    • Two Sample t-test - 图16:样本方差
  1. 计算p-_value：
    选择一个显著性水准Two Sample t-test - 图17，一般为0.01，0.05，0.1，然后根据Two Sample t-test - 图18和自由度Two Sample t-test - 图19,去找到相应的_p    -value。可以去查t界值表或者通过程序计算出来。

实例计算

以之前乌龟为例，若样本数据为：

  • 样本大小： Two Sample t-test - 图20， Two Sample t-test - 图21
  • 样本均值： Two Sample t-test - 图22
  • 样本标准差： Two Sample t-test - 图23

建立检验假设，检验水准

  • Two Sample t-test - 图24 ，即假设两物种乌龟总体平均重量相等
  • Two Sample t-test - 图25，即两物种乌龟总体平均重量不相等
  • Two Sample t-test - 图26

计算t检验统计量：
Two Sample t-test - 图27

Two Sample t-test - 图28

Two Sample t-test - 图29
以Two Sample t-test - 图30 为输T Score to P Value Calculator计算，可得出Two Sample t-test - 图31。

确定结论
Two Sample t-test - 图32， 故不拒绝零假设Two Sample t-test - 图33，差异无统计学意义。没有充分理由说明两个乌龟物种的平均重量不相等。

Python 代码实现

一般常见的算法，都是有Python库封装好的了，我们直接调用它给的接口就行了。
这里借助一个Python科学计算库 scipy, 一般可以通过命令pip install scipy安装。

  1. import numpy as np
  2. import scipy.stats as stats
  4. ## 研究者想知道两种植物的平均高度是否相等，所以他们各搜集了20株植物
  5. ## group1,group2分别为两个植物样本身高
  6. group1 = np.array([14, 15, 15, 16, 13, 8, 14, 17, 16, 14, 19, 20, 21, 15, 15, 16, 16, 13, 14, 12])
  7. group2 = np.array([15, 17, 14, 17, 14, 8, 12, 19, 19, 14, 17, 22, 24, 16, 13, 16, 13, 18, 15, 13])
  9. # 确定总体方差是否相等
  10. # 根据经验，如果较大的样本方差与较小的样本方差之比小于4：1，我们可以假定总体具有相同的方差。
  11. print(np.var(group1), np.var(group2))
  12. # 7.73 12.26  # 12.26 / 7.73 = 1.586，小于4。这意味着我们可以假设总体方差相等
  15. ## 通过stats.ttest_ind 进行两样本t检验
  16. res = stats.ttest_ind(a=group1, b=group2, equal_var=True)
  17. print("t statistic: ", res.statistic)
  18. print("P Value: ", res.pvalue)
  19. ## output
  20. ## t statistic:  -0.6337397070250238
  21. ## P Value:  0.5300471010405257

stats.ttest_ind 的参数a和b分布是第一个样本和第二个样本；equal_var只两个总体方差是否相等。默认为True，若为False可使用Welch’s t-test

结果说明：

Two Sample t-test - 图34,假设两种植物平均高度相等
Two Sample t-test - 图35,该植物平均高度不相等

因为此次检验p-value(0.53005) 大于 Two Sample t-test - 图36, 不能拒绝Two Sample t-test - 图37,所以没有充分的证据说明两植物的平均高度不同。

R代码

t-test在R里使用t.test进行计算

  1. > group1 <- c(14, 15, 15, 16, 13, 8, 14, 17, 16, 14, 19, 20, 21, 15, 15, 16, 16, 13, 14, 12)
  2. > group2 <- c(15, 17, 14, 17, 14, 8, 12, 19, 19, 14, 17, 22, 24, 16, 13, 16, 13, 18, 15, 13)
  3. > ?t.test
  4. > t.test(group1, group2, alternative = "two.sided", var.equal = T, mu=0)
  6.     Two Sample t-test
  8. data:  group1 and group2
  9. t = -0.63374, df = 38, p-value = 0.53
  10. alternative hypothesis: true difference in means is not equal to 0
  11. 95 percent confidence interval:
  12.  -2.726335  1.426335
  13. sample estimates:
  14. mean of x mean of y 
  15.     15.15     15.80

t.test 中的参数设置：

  • alternative设置备择假设的单双尾检验，默认为”two.sided” ,双尾检验，单位设置成”greater”或”less”
  • 参数mu，为两总体的差异均值，这里设为0，因为假设了两总体均值相等。所以差值为0。
  • var.equal, 两总体方差是否相等

最后的结果和Python中的一样，甚至更详细。

参考

Two Sample t-test: Definition, Formula, and Example