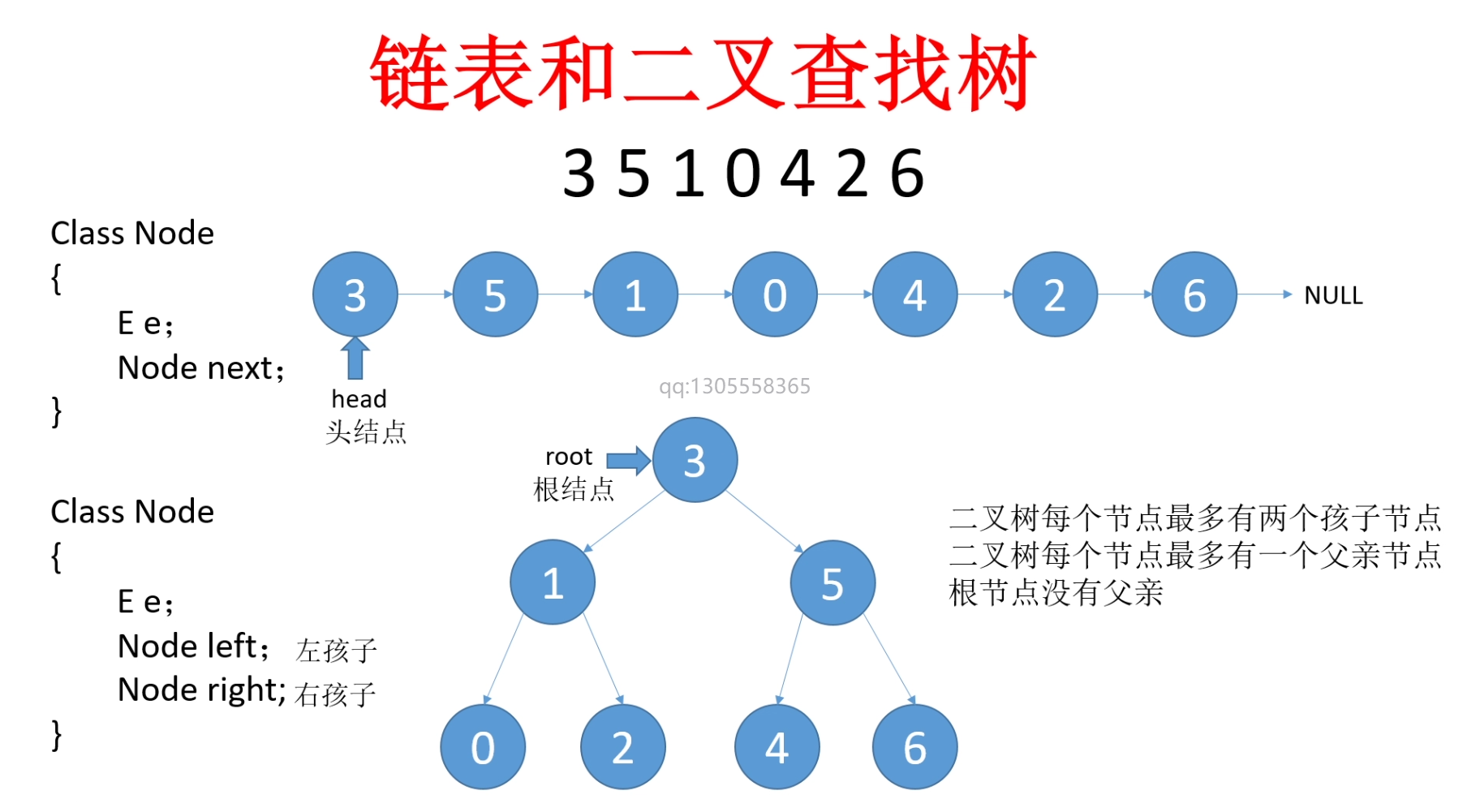
具有下列性质的二叉树：

  1. 左子树上所有节点的值均小于它的根节点的值
  2. 右子树上所有节点的值均大于它的根节点的值
  3. 任意节点的左、右子树也分别为二叉查找树
  4. 没有相等的节点

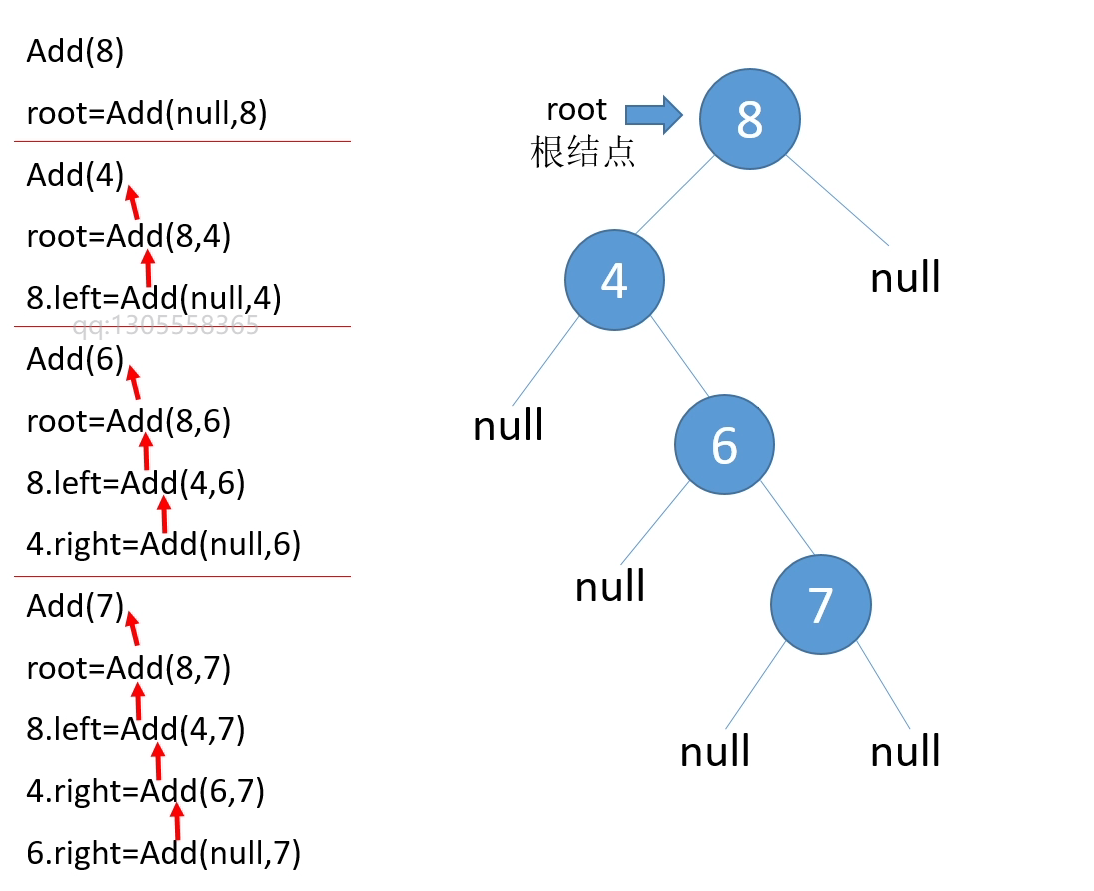
image.png

二叉树的元素添加：

公有修饰符 Add是依附于私有修饰符 Add的。 假设添加 8、4、6、7 四个元素： （1）Add（8）➡ Add（null，8）➡ 由于 node 为空，所以容量加一，8 将会作为根节点进行返回。 （2）Add（4）➡ Add（8，4）➡ 由于 8 大于 4 ，8.left = Add（8.left==null，4）➡由于 8.left 为空，所以 4将作为 8 的左孩子。 （3）Add（6）➡ Add（8，6）➡ 由于 8 大于 6，8.left = Add（8.left==4，6）➡由于 4 小于 6 ，4.right = Add（4.right==null，6），最后 Add（null，6），6 将作为 4 的右孩子节点 （4）Add（7）➡ Add（8，7）➡ 由于8 大于 7，8.left = Add（8.left==4，7）➡ 由于4小于7，4.right= Add（4.right==6，7）➡由于 6 大于 7 ，6.right = Add（6.right==null，7），最后Add（null，7），7 将作为 6 的右孩子节点。

image.png

  1. class BST1<E> where E : IComparable<E> 
  2.     {
  3.         private class Node
  4.         {
  5.             public E e;
  6.             public Node left;
  7.             public Node right;
  9.             public Node(E e)
  10.             {
  11.                 this.e = e;
  12.                 left = null;
  13.                 right = null;
  14.             }
  15.         }
  17.         private Node root;
  18.         private int N;
  20.         public BST1()
  21.         {
  22.             root = null;
  23.             N = 0;
  24.         }
  26.         public int Count { get { return N; } }
  28.         public bool IsEmpty { get { return N == 0; } }
  30.         /// <summary>
  31.         /// 非递归方式的二叉树添加元素
  32.         /// </summary>
  33.         /// <param name="e">添加的元素</param>
  34.         public void add(E e)
  35.         {
  37.             //如果根节点未空，就调用 Node 的构造函数，并作为根节点
  38.             //容量加一，退出这个方法
  39.             if (root == null)
  40.             {
  41.                 root = new Node(e);
  42.                 N++;
  43.                 return;
  44.             }
  46.             Node pre = null;
  47.             Node cur = root;
  49.             //只要 cur 不为空就一直循环
  50.             //（1）如果添加的元素跟 cur.e 的节点一致就跳出这个循环
  51.             //（2）如果添加的元素小于 cur.e 的节点， cur 的左节点就是 cur，否则 cur 的右节点就是 cur
  52.             //找到了一个空的位子跳出循环
  53.             //（1）调用 Node 的构造函数，传进来的 e ，就是要添加的元素，并且在 cur 的位子上，因为 cur 为空
  54.             //（2）在判断添加的元素是否小于 pre(就是cur 的上一个节点，这里是确定 cur 是父节点的左孩子还是右孩子) 的节点，那 pre 的左孩子就是 cur，否则右孩子就是 cur
  55.             //最后容量加一
  56.             while (cur != null)
  57.             {
  58.                 if (e.CompareTo(cur.e) == 0)
  59.                     return;
  61.                 pre = cur;  //pre 记录 cur 上一个节点
  63.                 if (e.CompareTo(cur.e) < 0)
  64.                     cur = cur.left;
  65.                 else
  66.                     cur = cur.right;
  67.             }
  69.             cur = new Node(e);
  71.             if (e.CompareTo(pre.e) < 0)
  72.                 pre.left = cur;
  73.             else
  74.                 pre.right = cur;
  76.             N++;
  77.         }
  79.         /// <summary>
  80.         /// 递归方式的给二叉树添加元素
  81.         /// </summary>
  82.         public void Add(E e)
  83.         {
  84.             root = Add(root, e);
  85.         }
  87.         /// <summary>
  88.         /// 以node为根的树中添加元素e，添加后返回根节点node
  89.         /// </summary>
  90.         /// <param name="node">根节点</param>
  91.         /// <param name="e">添加的元素</param>
  92.         /// <returns>返回根节点</returns>
  93.         private Node Add(Node node, E e)
  94.         {
  95.             if (node == null)
  96.             {
  97.                 N++;
  98.                 return new Node(e);
  99.             }
  101.             if (e.CompareTo(node.e) < 0)
  102.                 node.left = Add(node.left, e);
  103.             else if (e.CompareTo(node.e) > 0)
  104.                 node.right = Add(node.right, e);
  106.             return node;
  107.         }
  109.         public bool Contains(E e)
  110.         {
  111.             return Contains(root, e);
  112.         }
  114.         /// <summary>
  115.         /// 以 node 为根的树是否包含元素 e
  116.         /// </summary>
  117.         private bool Contains(Node node, E e)
  118.         {
  119.             if (node == null)
  120.                 return false;
  122.             if (e.CompareTo(node.e) == 0)
  123.                 return Contains(node.left, e);
  124.             else if (e.CompareTo(node.e) < 0)
  125.                 return Contains(node.left, e);
  126.             else    //e.CompareTo(node.e) > 0
  127.                 return Contains(node.right, e);
  128.         }
  130. //前序遍历
  131.         public void PreOrder()
  132.         {
  133.             PreOrder(root);
  134.         }
  136.         /// <summary>
  137.         /// 前序遍历以 node 为根的二叉查找树
  138.         /// </summary>
  139.         private void PreOrder(Node node)
  140.         {
  141.             if (node == null)
  142.                 return;
  144.             Console.WriteLine(node.e);
  145.             PreOrder(node.left);
  146.             PreOrder(node.right);
  147.         }
  149. //中序遍历
  150.         public void InOrder()
  151.         {
  152.             InOrder(root);
  153.         }
  155.         //中序遍历以 node 为根的二叉查找树
  156.         private void InOrder(Node node)
  157.         {
  158.             if (node == null)
  159.                 return;
  161.             InOrder(node.left);
  162.             Console.WriteLine(node.e);
  163.             InOrder(node.right);
  164.         }
  166. //后序遍历
  167.         public void PostOrder()
  168.         {
  169.             PostOrder(root);
  170.         }
  172.         private void PostOrder(Node node)
  173.         {
  174.             if (node == null)
  175.                 return;
  177.             PostOrder(node.left);
  178.             PostOrder(node.right);
  179.             Console.WriteLine(node.e);
  180.         }    
  181. //层序顺序
  182.         public void LevelOrder()
  183.         {
  184.             Queue<Node> p = new Queue<Node>();
  185.             p.Enqueue(root);
  187.             while(p.Count != 0)
  188.             {
  189.                 Node cur = p.Dequeue();
  191.                 Console.WriteLine(cur.e);
  193.                 if (cur.left != null)
  194.                     p.Enqueue(cur.left);
  195.                 if (cur.right != null)
  196.                     p.Enqueue(cur.right);
  197.             }
  198.         }
  199.     }
  201. //在数组中添加元素
  202. class Program
  203.     {
  204.         private static void Main(string[] args)
  205.         {
  206.             int[] a = { 8, 4, 12, 2, 6, 10, 14 };
  208.             BST1<int> bst = new BST1<int>();
  210.             for (int i = 0; i < a.Length; i++) 
  211.                 bst.Add(a[i]);
  213.             bst.PreOrder();
  215.             Console.WriteLine();
  217.             bst.InOrder();
  219.             Console.WriteLine();
  221.             bst.PostOrder(); 
  223.             Console.WriteLine();
  225.             bst.LevelOrder();
  227.             Console.ReadKey();
  229.         }
  230.     }

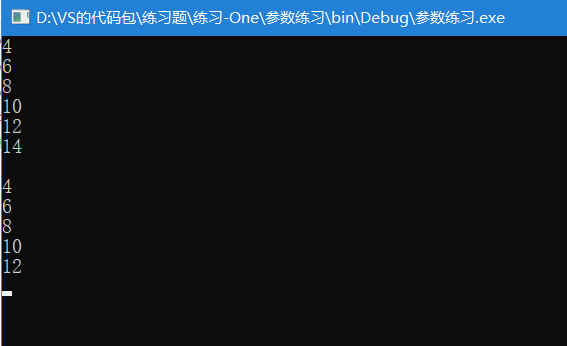
bst.PreOrder()的运行结果：（不管是Add或add添加元素的方法，他们的运行结果都是一致的）

image.png

bst.InOrder()的运行结果：

image.png

bst.postOrder()的运行结果：

image.png

bst.LevelOrder()的运行结果：

image.png

删除最大元素和最小元素

        ///////////////////////
        //          8              //
        //      /       \          //
        //     4        12       //
        //   /   \     /   \      //
        //  2     6   10   14 //
        ///////////////////////

首先查找最大、最小元素的节点，即最右边、最左边。 而查找到元素的方法也很简单，就一直返回调用 node.left ，直到 node.left 为空，说明左孩子已经没元素了，那当前节点元素就是最小的了。查找最大元素同理！ 首先，Min函数即是锁定最小的值，代码逻辑就是，往最左边一直走，直到 node.left 为空，此时只需返回 node即可。 然后就是 RemoveMin 函数，它的删除操作就是，赋值取代。第一步的操作 node.left = RemoveMin(node.left)；return node；直到 node.left 为空。最后的结果：返回 8 ； 具体逻辑：先传进来的 node = 8；那就是 4 = removemin（4）；return 8 ； 2 = removemin（2）；return 4； null = removemin（null）; return 2； 此时，2.left 为空；容量减一，并且 return null； 又因为锁定了 node = 2；就是最小，随后进行容量减一。 那现在 最左边就是 4 ；但是 此时的 4.left 还不为 null 所以当 4.left = removemin（4.left），而 removemin（4.left）返回一个 null ，也就完成了复制取代 4.left = null 4 = removemin（4）；return 8 ；知道了 removemin（4）返回了 4，也就验证了 4 = 4 ；return 8；

  // 寻找二叉查找树的最小元素
        public E Min()
        {
            if (IsEmpty)
                throw new ArgumentException("空树");

            return Min(root).e;
        }

        /// <summary>
        /// 返回以node为根的二叉查找树的最小值所在的节点
        /// </summary>
        private Node Min(Node node)
        {
            if (node.left == null)
                return node;

            return Min(node.left);
        }

        public E Max()
        {
            if (IsEmpty)
                throw new ArgumentException("空树");

            return Max(root).e;
        }

        /// <summary>
        /// 返回以node为根的二叉查找树的最大值所在的节点
        /// </summary>
        private Node Max(Node node)
        {
            if (node.right == null)
                return node;

            return Max(node.right);
        }

        public E RemoveMin()
        {
            E ret = Min();
            root = RemoveMin(root);
            return ret;
        }

        /// <summary>
        /// 删除掉以Node为根的二叉查找树中的最小节点
        /// 返回删除节点后新的二叉查找树的根
        /// </summary>
        private Node RemoveMin(Node node)
        {
            if (node.left == null)
            {
                N--;
                return node.right;
            }

            node.left = RemoveMin(node.left);
            return node;
        }

        public E RemoveMax()
        {
            E ret = Min();
            root = RemoveMax(root);
            return ret;
        }

        /// <summary>
        /// 删除掉以Node为根的二叉查找树中的最大节点
        /// 返回删除节点后新的二叉查找树的根
        /// </summary>
        private Node RemoveMax(Node node)
        {
            if (node.right == null)
            {
                N--;
                return node.left;
            }

            node.right = RemoveMax(node.right);
            return node;
        }

//Main函数中，删除最大、小元素
    class Program
    {
        private static void Main(string[] args)
        {
            int[] a = { 8, 4, 12, 2, 6, 10, 14 };

            BST1<int> bst = new BST1<int>();

            for (int i = 0; i < a.Length; i++) 
                bst.Add(a[i]);

            bst.RemoveMin();
            bst.InOrder();

            Console.WriteLine();

            bst.RemoveMax();
            bst.InOrder();
            Console.ReadKey();

        }
    }

运行结果：

image.png

任意删除元素

Remove 函数的运行逻辑： 调用 Remove(4); remove(8,4); if(4.compareTo(8) < 0){8.left = remove(4.4) return node} if(4.compareTo(4) == 0){if(4.left ==0)、if(4.right ==0);不符合条件，不运行。} 此时的Node为 4 node s = min(node.left) =>node s = min(6) => node s = 6; s.right = RemoveMin(node.right) =>6.right = removemin(6) => 6.right = null s.left = node.left => 6.left = 6.left => 6.left = null return s => return 6; 然后回到 8.left = remove(4.4) =>8.left = 6 return 8;

public void Remove(E e)
        {
            Remove(root, e);
        }

        /// <summary>
        /// 删除掉以Node为根的二叉查找树中的最大节点
        /// 返回删除节点后新的二叉查找树的根
        /// </summary>
        private Node Remove(Node node,E e)
        {
            //如果二叉树中没有要删除的元素节点，就直接返回 null
            if (node == null)
                return null;

            //当二叉树的根节点只有左（右）孩子时
            //如果要删除的元素（大）小于当前节点元素，那就意味着要删除的元素在左（右）边
            //跟 RemoveMin（RemoveMax） 函数同样的代码逻辑
            if (e.CompareTo(node.e) < 0)
            {
                node.left = Remove(node.left, e);
                return node;
            }
            else if (e.CompareTo(node.e) > 0)
            {
                node.right = Remove(node.right, e);
                return node;
            }
            else  //e.CompareTo(node.e)== 0
            {
                //假设 e 为 4.
                //那他的左右孩子分别为 2、6
                //也就不符合判断条件
                //跳出循环

                if (node.right == null)
                {
                    N--;
                    return node.left;
                }
                if (node.left == null)
                {
                    N--;
                    return node.right;
                }

                //要删除的节点左右都有孩子
                //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
                //用这个节点顶替待删除节点的位置

                //Node s = min（6）
                //Node s = 6
                //6.right = removemin(6) => null = removemin(6)
                //6.right = null
                //6.left = null
                Node s = Min(node.right);
                s.right = RemoveMin(node.right);
                s.left = node.left;
                return s;
            }
        }
}

class Program
    {
        private static void Main(string[] args)
        {
            int[] a = { 8, 4, 12, 2, 6, 10, 14 };

            BST1<int> bst = new BST1<int>();

            for (int i = 0; i < a.Length; i++) 
                bst.Add(a[i]);

            ///////////////////////
            //          8              //
            //      /       \          //
            //     4        12       //
            //   /   \     /   \      //
            //  2     6   10   14 //
            ///////////////////////
            ///
            bst.Remove(4);
            bst.InOrder();
            Console.ReadKey();

        }
    }

运行结果：

image.png

树的最高度和性能分析

树的最高度决定了二叉树的时间复杂度，按简单的来看，分为两种极端的情况：《最好情况》《最坏情况》 而二叉树的时间复杂度在O（Log N）- O（N） 之间 当添加的数据随机性越强，他的时间复杂度越趋近O（Log N），而添加的数据是有顺序的话那时间复杂度就是O（N），其查找的时间复杂度有是O（N） 当查找数据时，会忽略掉一些不需要查找的元素，其时间复杂度也是O（log N） 而我们查找到数据的最高度，是为了更好的看到当前的二叉树的时间复杂度

《最好情况》：
///////////////////////

        //          8              //

        //      /       \          //

        //     4        12       //

        //   /   \     /   \      //

        //  2     6   10   14 //

        ///////////////////////

《最坏情况》： //2-4-6-8-10-12-14 他们之间的时间复杂度： image.png

public int MaxHeight()
        {
            return MaxHeight(root);
        }

        private int MaxHeight(Node node)
        {
            if (node == null)
                return 0;

            //int l = MaxHeight(node.left);
            //int r = MaxHeight(node.right);
            return Math.Max(MaxHeight(node.left), MaxHeight(node.right)) + 1;
        }

   class Program
    {
        private static void Main(string[] args)
        {
            int[] a = { 8, 4, 12, 2, 6, 10, 14 };

            BST1<int> bst = new BST1<int>();

            for (int i = 0; i < a.Length; i++) 
                bst.Add(a[i]);

            ///////////////////////
            //          8              //
            //      /       \          //
            //     4        12       //
            //   /   \     /   \      //
            //  2     6   10   14 //
            ///////////////////////

            Console.WriteLine(bst.MaxHeight());
            Console.ReadKey();

        }
    }

运行结果：

image.png