手写题笔记

刚入门如何刷题，借知乎 lucifer 的一篇回答，小白刷题分为两个阶段，系统学习数据结构和算法只是，针对性刷题。以 LRU 缓存机制为例，有这样一个思考的过程，审题、抽象算法模型、根据模型选取合适的数据结构和算法。

1. 看完题目，要抓住一个或两个其中的核心点。LRU 的核心点在于删除最久未使用、O(1)时间。
2. 这道题是设计题，只需要填充功能，模型就不需要我们设立了。
3. LRU 中涉及 get/put 操作，获取/添加数据，那么肯定需要一个数据结构保存数据，数组？链表，单向还是双向？循环还是不循环？哈希表？回到a，需要满足常数时间，那么数组、链表就不行，数组没法在常数时间内做到更新、删除，链表没法在常数时间内做到查找、更新、删除。而哈希表是无序的，就没有实现最久未使用。那只有考虑组合多种数据结构了。
4. 优化。使用哈希表的话，空间是线性的，如果无法接受，可以设置存档点。可以将空间变为常数，时间变为斜率更小的线性，增加的存档点越多，时间的斜率就更小。其实这是一种跳表的实现思路，在工程实践中很常见，是一种取舍。

   数组

   简单题

   26. 删除有序数组中的重复项

   题目说明，删除数组中的重复项，要求原地修改，也就是空间O(1)，返回值是修改后数组不重复项的个数。力扣是对这个数组进行去重，然后根据返回的个数，去遍历比较的数组，以这样的方式来判断的。
   考察知识点，数组、双指针（读写/快慢指针）、数组为空。
   读写指针的主要思路，遍历数组的下标作为读指针，设置一个写指针，当读指针不等于写指针指向的数值时，移动写指针并修改指向数值。写指针初始化为0，读指针在循环初始化语句中初始化为1，最后返回不重复项个数，即 slow + 1。

   var removeDuplicates = function(nums) {
   let slow = 0, len = nums.length;
   for (let i = 1; i < len; i++) {
     if (nums[i] !== nums[slow]) {
         nums[++slow] = nums[i];
     }
   }
   return slow + 1;
   };

   剑指 Offer 29. 顺时针打印矩阵

   
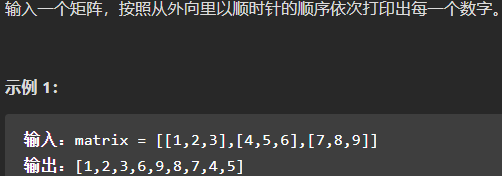
   考察知识点，数组边界，分解问题，模拟实现的能力。
   变相的也是一种区间问题。多个变量维护水平方向和垂直方向的区间。区间处理不好的话，就很头痛，代码量是不多的，而且很有规律。

   var spiralOrder = function(matrix) {
   const ret = [];
   let top = 0, right = (matrix[0] ? matrix[0].length : 0) - 1, bottom = matrix.length - 1, left = 0;
   while(top <= bottom && left <= right) {
     // 从右到左
     for (let column = left; column <= right; column++) {
         ret.push(matrix[top][column]);
     }
     for (let row = top + 1; row <= bottom; row++) {
         ret.push(matrix[row][right]);
     }
     if (top >= bottom || left >= right) break; 
     for (let column = right - 1; column > left; column--) {
         ret.push(matrix[bottom][column])
     }
     for (let row = bottom; row > top; row--) {
         ret.push(matrix[row][left]);
     }
     top++; bottom--; left++; right--;
   }
   return ret;
   };

   169. 多数元素

   
   考察的数据结构并不多，就是数组指针、哈希表。但是考察的算法是真的多，可以用“排序”、“分治-递归实现”、“投票算法”。
   数组指针+哈希表，10分钟搞出来。很简单的思路，首先遍历数组，进行计数。然后再遍历一次哈希表，用值和阈值进行比较，找到了大于阈值的键就保存下来并终止循环。返回大于阈值的键，就是要找的数字了。

   var majorityElement = function(nums) {
   let hash = {};
   for (let num of nums) {
     if (!(num in hash)) hash[num] = 0;
     hash[num]++;
   }
   let maxKey = 0, bound = Math.floor(nums.length / 2);
   for (let [k, v] of Object.entries(hash)) {
     if (v > bound) {
         maxKey = k;
         break;
     }
   }
   return maxKey;
   };

   时间空间都是O(n)。

投票算法
这个算法只有在题目条件下，才能用上。众数出现的次数大于 nums.length / 2，为什么不足满这个条件就用不了投票算法？
投票算法的详细步骤是，设置一个候选众数marjority，以及计数器count，marjority初始化数组任一个数，count为0。遍历数组，每一轮，首先都判断count，为0，当前元素赋值给marjority。\
然后判断marjority与num[i]，如果相同则count++，否则，count—。整个算法过程中，count 不为负。
这个算法的思路是，遇到相同的数字就加票，数字不同的时候就减票，直到票数为0，那么就会重置一次候选众数。跟分治的思想有点像，也相当于把数组划分为了多个区间。这样划分到最后，就剩一个数字，这个数字就是满足题目的数字了。

var majorityElement = function(nums) {
    let marjority = nums[0], count = 1;
    for (let i = 1, len = nums.length; i < len ; i++) {
        if (count === 0) marjority = nums[i];
        if (marjority === nums[i]) count++;
        else count--;
    }
    return marjority;
};

时间O(n)，空间O(1)。

414. 第三大的数

，这个数组最多可以有1w个数字。
考察的知识点，挺多的，排序、有序集合、三指针（一次遍历）。
排序的话就比较简单，但是排序算法上的选择还是有讲究的，尽量选择时间在O(nlogn)的。题解如下：

var thirdMax = function(nums) {
    nums.sort((a,b) => b - a);
    for (let i = 1, diff = 1, len = nums.length; i < len; i++) {
        if (nums[i] !== nums[i-1] && ++diff === 3) return nums[i];
    }
    return nums[0];
};

时间O(nlogn)，空间O(logn)。
三指针-一次遍历
遍历数组，用3个变量保存最大、次大、第三大的值，然后模拟有序集合的插入、删除操作。主要思路，初始化3个变量为最小的负值(-Number.MAX_VALUE)。如何保证有序呢？答案就是，划分区间。3个值，可以划分出4个区间，比c小，c-b，b-a，比a大。只有右边三个区间去需要做赋值，落入这3个区间的话，每次都从第三个大的值开始，将上一个大的值覆盖过来。

var thirdMax = function(nums) {
    let firstBigNum = -Number.MAX_VALUE, secondBigNum = -Number.MAX_VALUE, thirdBigNum = -Number.MAX_VALUE;
    for (let i = 0, len = nums.length; i < len; i++) {
        if (nums[i] > firstBigNum) {
            thirdBigNum = secondBigNum; secondBigNum = firstBigNum; firstBigNum = nums[i];
        } else if (firstBigNum > nums[i] && nums[i] > secondBigNum) {
            thirdBigNum = secondBigNum; secondBigNum = nums[i];
        } else if (secondBigNum > nums[i] && nums[i] > thirdBigNum) {
            thirdBigNum = nums[i];
        }
    }
    return thirdBigNum === -Number.MAX_VALUE ? firstBigNum : thirdBigNum;
};

时间O(n)，空间O(1)。

283. 移动零

考察，数组指针、双指针、原地置换（原地修改）。这道题要求原地操作，那么可以原地置换（力扣解法）或者原地修改。主要思路，快慢指针，slow指向0，fast指向非零，然后再遍历一次slow到fast的数组区间，将fast指向的值赋值给slow。最后将slow到数组末尾的值置0。

var moveZeroes = function(nums) {
    let slow = 0, fast = 0, len = nums.length;
    for (; fast < len; fast++) {
        if (nums[fast] !== 0) nums[slow++] = nums[fast];
    }
    while(slow < len) nums[slow++] = 0;
};

时间O(n)，空间O(1)。虽然时间是常数，但是整个数组其实遍历了两次，第一个循环中，fast遍历了一遍，slow遍历了一部分，第二个需要slow将剩下的部分也遍历完了。

118. 杨辉三角

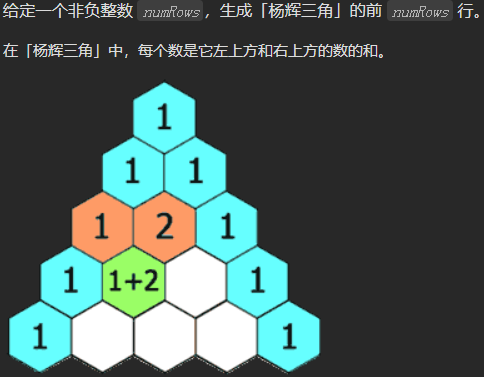
这个杨辉三角只需要计算左上角元素和同列的上一个元素之和。不是另一个杨辉三角，这个还算简单。
考察知识点，二维数组、指针控制。
我的解法就比较常规，两层循环来计算每层每个数的数值，然后添加进结果数组中。

var generate = function(numRows) {
    const ret = [];
    for (let row = 0; row < numRows; row++) {
        let sub = [1];
        for (let i = 1; i <= row; i++) {
            sub[i] = ret[row-1][i-1] + (ret[row-1][i] ? ret[row-1][i] : 0);
        }
        ret.push(sub);
    }
    return ret;
};

时间O(n^2)，空间O(n^2)。空间这个没得法，就是返回二维数组。

中等题

695. 岛屿的最大面积

https://www.yuque.com/heyao-uthnw/gr9otg/oku1ck#aZfU3

209. 长度最小的子数组

输入 7，[2,3,1,2,4,3]。输出2。
考察知识点，数组、数组中所有值之和都不大于target的情况、前缀和、二分查找、双指针（滑动窗口）。
首先来一发暴力求解。分析哈，先要找出满足条件的子数组，需要两层循环确定子数组的首尾索引，然后再加一层遍历，求姐子数组的和。再更新最小值。

var minSubArrayLen = function (target, nums) {
    const len = nums.length;
    let sum = 0, minLen = len + 1;
    for (let i = 0; i < len; i++) {
        for (let j = i; j < len; j++) {
            sum = 0;
            for (let k = i; k <= j; k++) {
                sum += nums[k];
            }
            if (sum >= target) {
              minLen = Math.min(minLen, j - i + 1);
              break;
            }
        }
    }
    return minLen > len ? 0 : minLen;
};

时间优化，3重循环，最内层计算子数组的和，子数组的很多部分其实是重复的。可以利用一个数组，将前缀和保存下来，将第3层循环舍弃掉，这样可以将时间降到O(n^2)。此时，可以通过力扣了。

var minSubArrayLen = function (target, nums) {
    const len = nums.length, prefixSum = new Array(len).fill(0); // prefixSum[i] 表示[0,i-1]之间的和。
    let sum = 0, minLen = len + 1;
    for (let i = 0; i < len; i++) {
        for (let j = i; j < len; j++) {
            sum = 0;
            if (j > 0 && prefixSum[j] === 0) prefixSum[j] = prefixSum[j-1] + nums[j-1];
            sum = prefixSum[j] - prefixSum[i] + nums[j];
            if (sum >= target) {
                minLen = Math.min(minLen, j - i + 1);
                break;
            }
        }
    }
    return minLen > len ? 0 : minLen;
};

其实不用3层循环哈，看了力扣题解知道，两层循环，也能计算出最大连续和的最小长度子数组。

var minSubArrayLen = function(target, nums) {
  const len = nums.length;
  let sum = 0, minLen = len + 1;
  for (let i = 0; i < len; i++) {
    sum = 0;
    for (let j = i; j < len; j++) {
      sum += nums[j];
      if (snum >= target) {
        minLen = Math.min(minLen, j - i + 1);
        break;
      }
    }
  }
  return minLen > len ? 0 : minLen;
}

继续优化，还是可以用到前缀和，不过使用方式就变了，在前缀和的基础上进行二分查找。这个不懂，没弄出来，明天继续。

48. 旋转图像

还是比较简单的。考察知识点，数组指针、原地操作、二维数组的上三角遍历、主副对角线对称坐标的计算、边界。解决的方法就是对角线置换，然后再对折置换。有两条线路可以选，第一，主对角线+垂直方向对称，第二，副对角线+水平方向对称。我选择第二条，水平方向对称置换的时候很舒服，就是副对角线的坐标计算稍微饶了一些。
需要注意的是左上三角的遍历，就是i、j的边界值，坐标计算公式。

var rotate = function (matrix) {
    const n = matrix.length;
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n - 1 - i; j++) {
            if (i + j >= n - 1) break;
            swapNum(matrix, i, j, n - 1 - j, n - 1 - i);
        }
    }
    for (let i = 0, bound = Math.floor(n / 2); i < bound; i++) swapRow(matrix, i, n - 1 - i);
};
var swapNum = function (array, ai, aj, bi, bj) {
    const tmp = array[ai][aj];
    array[ai][aj] = array[bi][bj];
    array[bi][bj] = tmp;
}
var swapRow = function (array, rowA, rowB) {
    const tmp = array[rowA];
    array[rowA] = array[rowB];
    array[rowB] = tmp;
}

时间O(n^2)，空间O(1)，虽然只遍历了半个矩阵，但是时间复杂度还是这么多哈。

33. 搜索旋转排序数组

比较注重二分，放在二分查找里。

链表

简单题

21. 合并两个有序链表

考察知识点，递归、指针操作、双指针。需要注意链表的边界情况，①其中一条为空，另一条不为空，②两条都为空。
递归解法主要思路，递归函数返回值是节点，list1.val <= list2.val 时递归 list1.next 与 list2，并返回 list1，另一个大于的情况就反过来。注意特殊情况，当 list1 或 list2 为空的时候，就返回另一个节点。这样最终返回的节点也就是合并后的链表头节点。

var mergeTwoLists = function(list1, list2) {
    if (!list1) return list2;
    if (!list2) return list1;
    if (list1.val <= list2.val) {
        list1.next = mergeTwoLists(list1.next, list2);
        return list1;
    } else {
        list2.next = mergeTwoLists(list1, list2.next);
        return list2;
    }
};

双指针的主要思路，先创建一个哑节点 dummyHead 和当前节点 cur，while 迭代两个链表 list1、list2，当其中一个链表为空时终止迭代，在循环中判断两链表节点的大小，赋值 cur.next，并移动 list1、list2、cur。最后需要注意其中一个链表非空的情况，cur = list1 ? list1 : list2 即可。

var mergeTwoLists = function(list1, list2) {
    const dummyHead = new ListNode(-1);
    let cur = dummyHead;
    while(list1 && list2) {
        if (list1.val <= list2.val) {
            cur.next = list1;
            list1 = list1.next;
        } else {
            cur.next = list2;
            list2 = list2.next;
        }
        cur = cur.next;
    }
    cur.next = list1 ? list1 : list2;
    return dummyHead.next;
};

中等题

2. 两数相加

链表版本的大数相加，和字符串相加一样的思路。就是需要处理链表这种结构，其实就是其中一个链表节点为空、两个链表为空但进位有值的两种情况。
考察，哑节点简化技巧、循环条件、进位标志 carryFlag、空节点的处理。
思路就是设置一个cur指针用来连接新链表，遍历两个链表的时候，用node指针指向存值的节点，将3个值进行相加取余、除法，将取余的值复制给 node.val，除法的商赋值给 carryFlag。然后再移动3个指针，cur、l1、l2。

var addTwoNumbers = function(l1, l2) {
    const dummyHead = new ListNode(-1);
    let cur = dummyHead, plus = 0, node;
    while(l1 || l2 || plus) {
        node = l1 ? l1 : l2;
        if (!node) node = new ListNode();
        let left = l1 ? l1.val : 0, right = l2 ? l2.val : 0;
        node.val = (left + right + plus) % 10;
        plus = Math.floor((left + right + plus) / 10);
        cur.next = node;
        l1 = l1 && l1.next;
        l2 = l2 && l2.next;
        cur = cur.next;
    }
    return dummyHead.next;
};

82. 删除排序链表中的重复元素 II

比较简单，考察，哑节点简化、遍历链表、重复值标志repetition、尾节点置空来断链。
设置一个cur指向哑节点，用来连接链表，遍历时首先比较 repetition，然后再比较 head 当前值与下一个节点，相同时赋值repetition。最后连接 cur.next，移动 cur、head。链表处理完记得设置 cur.next 为空，不然仍连接着链表中原来的节点，没有断开。

var deleteDuplicates = function(head) {
    const dummyHead = new ListNode(-1);
    let cur = dummyHead, repetition = Number.MAX_VALUE;
    while(head) {
        if (head.val === repetition) {
            head = head.next; continue;
        }
        if (head.next && head.next.val === head.val) {
            repetition = head.val; continue;
        }
        cur.next = head;
        cur = cur.next;
        head = head.next;
    }
    cur.next = null;
    return dummyHead.next;
};

445. 两数相加 II

知识迁移能力确实重要，没有一点联想能力。两数相加的低位从链表头开始，这道题的低位从链表尾开始。
考察，链表指针、哑节点简化、进位标志、节点为空的边界情况、反转链表、栈、尾插法。
有一种思路很简单，先反转再相加再反转。这样的时间是O(3m+2n），m是两链表较长的长度。空间是O(1)。

var addTwoNumbers = function(l1, l2) {
    l1 = reverseList(l1); l2 = reverseList(l2);
    const dummyHead = new ListNode(-1);
    let cur = dummyHead, carry = 0;
    while(l1 || l2 || carry) {
        let node = l1 ? l1 : l2;
        if (!node) node = new ListNode();
        let left = l1 ? l1.val : 0;
        let right = l2 ? l2.val : 0;
        node.val = (left + right + carry) % 10;
        carry = Math.floor((left + right + carry) / 10);
        cur.next = node;
        cur = cur.next;
        l1 = l1 && l1.next;
        l2 = l2 && l2.next;
    }
    dummyHead.next = reverseList(dummyHead.next);
    return dummyHead.next;
};
var reverseList = function(list) {
    let cur = list, pre = null, next = list.next;
    while(cur) {
        next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}

第二种解法，逆序应该想到栈，这是一种思路。用栈保存节点值，然后弹出进行相加，每次相加的结果插入到哑节点后面。用栈的好处是没有改变来那边的结构，虽然空间上到了O(m+n)。时间是O(2m+2n)。

var addTwoNumbers = function(l1, l2) {
    const stk1 = [], stk2 = [], dummyHead = new ListNode();
    let carry = 0;
    while(l1) {stk1.push(l1.val); l1 = l1.next;}
    while(l2) {stk2.push(l2.val); l2 = l2.next;}
    while(stk1.length || stk2.length || carry) {
        let left = stk1.length ? stk1.pop() : 0;
        let right = stk2.length ? stk2.pop() : 0;
        let node = new ListNode((left + right + carry) % 10);
        carry = Math.floor((left + right + carry) / 10);
        node.next = dummyHead.next;
        dummyHead.next = node;
    }
    return dummyHead.next;
};

栈

简单题

20. 有效的括号

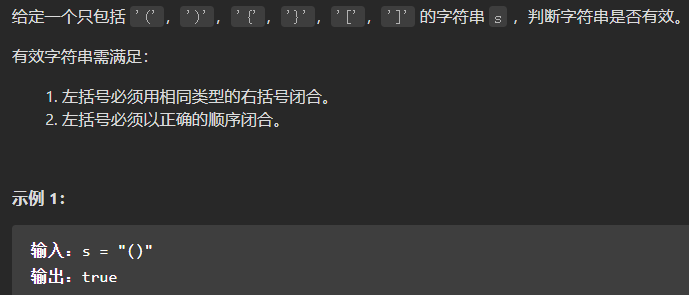
考察知识点，栈。
主要思路。用一个对象保存三种右括号为键，左括号为相应的值。初始化一个数组作为栈，遇到左括号就压栈，遇到右括号就出栈，从哈希表中取出当前右括号对应的左括号与栈顶元素比较。其中有3种情况需要注意，①当前右括号在哈希表中的值与栈顶元素不相等；②字符串为连续左括号；③字符串为连续右括号。

var isValid = function(s) {
    const kuohao = {
        ')':'(',
        ']':'[',
        '}':'{'
    }, stack = [];
    for (let c of s) {
        if (!(c in kuohao)) {
            stack.push(c);
        } else {
            if (stack.pop() !== kuohao[c]) return false;
        }
    }
    return stack.length === 0; // 为防止字符串为连续左括号的情况。
};

如果题目要求只匹配一种括号的话，空间复杂度可以降低为O(1)。使用计数器，不用栈。用栈和键值对象只是为了处理多种类型的括号。像C++语言还可以通过计数并改变字符串本身的方法，使这道题的空间复杂度降为O(1)，很巧妙。js 就不行，因为 js 无法改变字符串本身。

class Solution {
public:
    bool isValid(string s) {
        int top = -1;
        for(int i =0;i<s.length();++i){
            if(top<0 || !isMatch(s[top], s[i])){
                ++top;
                s[top] = s[i]; // 必须得修改字符串，其实s有效的话，top会一直在第-1、0之间反复横跳，最后还是-1。
            }else{
                --top;
            }
        }
        return top == -1;
    }
    bool isMatch(char c1, char c2){
        if(c1 == '(' && c2 == ')') return true;
        if(c1 == '[' && c2 == ']') return true;
        if(c1 == '{' && c2 == '}') return true;
        return false;
    }
};

232. 用栈实现队列

首先得知道队列常用的方法，push/pop/peek/isEmpty。用栈来实现队列。考察，栈和队列的特点、入栈和出栈。
主要思路，用两个数组来模拟栈，一个 count 变量保存队列长度。入队时压入栈1，出队和peek时检查栈2长度，如果为空，就将栈1的元素倒进来。判空更简单了，就判断 count 是否为0。这样的话应该不算O(1)时间了，因为可能存在一次O(n)的操作。

var MyQueue = function() {
    this.stack1 = [];
    this.stack2 = [];
    this.count = 0;
};
MyQueue.prototype.push = function(x) {
    this.stack1.push(x);
    this.count++;
};
MyQueue.prototype.pop = function() {
    if (this.count <= 0) return;
    if (!this.stack2.length) {
        while(this.stack1.length) this.stack2.push(this.stack1.pop());
    }
    this.count--;
    return this.stack2.pop();
};
MyQueue.prototype.peek = function() {
    if (this.count <= 0) return;
    if (!this.stack2.length) {
        while(this.stack1.length) this.stack2.push(this.stack1.pop());
    }
    return this.stack2[this.stack2.length-1];
};
MyQueue.prototype.empty = function() {
    return this.count === 0;
};

还有另一种思路是入队的时候倒弄两个栈。这样push的时间总是O(n)。出队的时候倒弄，pop 的摊还时间是O(1)。这个摊还分析还是挺顶的。

中等题

227. 基本计算器 II

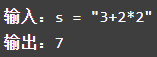，整数除法仅保留整数部分，忽略小数。字符串中包含空格、数字、运算符。不包含括号。
考察，栈的使用、区分+-和/的操作、负数取整、简化操作、字符串转换为数值。
区分+-、/的思路是，遍历当前字符，如果是字符是数值，就继续遍历下一个字符，将连续的数值转换出来。如果是空格就跳过。主体思路是计算/的结果，然后压入栈中，最后对栈中的数值进行累加。
如果是运算符就判断 pre_flag，处理当前字符的操作数是比较难的，取数也难取，遍历也被打乱顺序。所以处理上一个运算符的逻辑。+就入栈，-就将数值取负入栈，就将栈中的数值与当前数相乘，/尤其需要注意，js 中只有位运算可以忽略小数部分，其他的取整在负数的时候都有影响，比如向下取整，-3/2就会变成-2，与题目要求不符。

var calculate = function(s) {
    let pre_flag = '+', num = 0, stack = [];
    s += '$';
    for (let c of s) {
        if (!Number.isNaN(Number(c)) && c !== ' ') {
            num = num * 10 + (+c);
        } else if (c === ' ') {
            continue;
        } else {
            switch(pre_flag) {
                case '+': stack.push(num);break;
                case '-': stack.push(-num);break;
                case '*': stack.push(stack.pop() * num);break;
                case '/': stack.push((stack.pop() / num) | 0);break;
            }
            pre_flag = c;
            num = 0;
        }
    }
    let ans = 0;
    while(stack.length) ans += stack.pop();
    return ans;
};

71. 简化路径

总的来说就是返回一个绝对路径，只有小写字符、数字、/、_、.、组成。对输入的路径字符串进行处理，主要就做2个操作，如果是路径是一个点就跳过，两个点就返回上一级目录，其余的情况都是正常路径。返回绝对路径的最后一个字符不能是斜杠。
考察，如何简化问题、如何全面考虑问题，栈的使用倒是其次。首先我想到的是遍历字符串，用索引的方式对每个字符进行判断，入栈出栈也是以字符为单位，这种粒度很细，就导致难以处理。将粒度划分粗一些，其实更好处理。以斜杠为分隔符，这样的话，就能明确每一个具体的子路径。当子路径是一个点、两个点的时候就可以简单直接的进行处理。
粒度的划分很重要，对于简化问题。还有一个简化操作是最后才添加斜杠。
其实这道题要考虑的问题不是很多。总的来说只有4种情况，当以子路径为粒度思考的时候要容易总结的多，① 子路径部分为空字符串（连续斜杠的话，两斜杠中间就没有值，注意是空字符串，不是空格字符串），② 一个点，③ 两个点，④ 其余情况都入栈。

var simplifyPath = function (path) {
    let strs = path.split('/'), stack = [];
    for (let c of strs) {
        if (c === '.' || c === '') continue;
        if (c === '..') {
            stack.pop();
        } else {
            stack.push(c);
        }
    }
    return '/'+stack.join('/');
};

如果以每个字符为粒度的话，也需要做一个子路径部分范围的查找限定，要有两个指针去限定子路径的首尾。这是一种方法。

503. 下一个更大元素 II

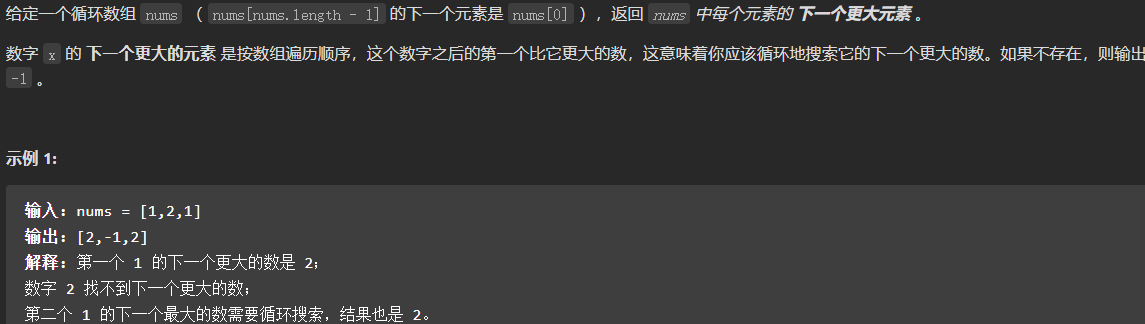
例子简单，就更需要全面的考虑问题。这道题的知识点太多了，考察了，“单调栈、保存索引、初始化技巧、拉直循环数组”。单调栈就是保存的值呈单调趋势，单调上升或下降，这题就需要单调不升的顺序。保存索引，我也想到过一点，但是没能进行下去。拉直循环数组，一般能想到的都是对下标做取余，这道题不需要遍历最后一个元素两次。
这道题单调栈保存的是数组值得索引，当前值大于栈顶元素时，将返回数组中数组索引对应的值保存为当前值，然后弹出栈顶元素，这个过程持续执行直到小于或者栈为空。这个循环过程结束后，将当前值的索引入栈。
这样的一个过程肯定是在遍历数组的过程中进行的。因为是循环数组，从索引1开始的元素都有可能需要绕一圈到它的前一个元素才能知道第一个比他大的值。所以遍历的话就需要遍历 2*n-1 次。

var nextGreaterElements = function(nums) {
    let len = nums.length, ret = new Array(len).fill(-1), stk = [];
    for (let i = 0, n = len * 2 - 1; i < n; i++) {
        while(stk.length && nums[stk[stk.length-1]] < nums[i % len]) {
            ret[stk[stk.length - 1]] = nums[i % len];
            stk.pop();
        }
        stk.push(i % len);
    }
    return ret;
};

时间是O(n)，除了最后一个元素，其他元素都要遍历两次，这样的一个耗时其实是O(2n)，每一次都要入栈出栈，所以耗时应该是O(4n)。空间是O(n)。

907. 子数组的最小值之和

这题太tm难了。一点想法都没有。。。

队列

中等题

103. 二叉树的锯齿形层序遍历

https://www.yuque.com/heyao-uthnw/gr9otg/oku1ck#jkC4g。解题在搜索专题。因为考察的重点更在BFS。

哈希表

简单题

1. 两数之和

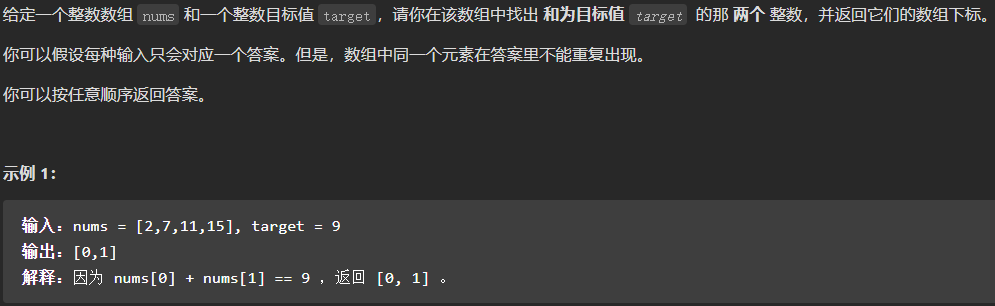
考察知识点，哈希表。
主要思路，初始化一个键值对存储对象，遍历数组nums，num（当前数值）查不到，就以target-num为键保存当前值索引。\
当num查得到的时候，就取出满足条件的另一个数的下标，返回两个数的下标即可。
注意，js 中的遍历方法只有 for、while、异常、every、some、find、findIndex、filter 可以中止或跳出循环。

var twoSum = function(nums, target) {
    const map = {};
    for (let i = 0, len = nums.length; i < len; i++) {
        if (!map.hasOwnProperty(nums[i])) {
            map[target-nums[i]] = i;
        } else {
            return [map[nums[i]], i];
        }
    }
};

387. 字符串中的第一个唯一字符

找到第一个不重复的字符，返回索引，没有这样的字符就返回-1。题目很简单，解决方法倒挺多的。
考察，哈希表的键值对存储活用、辅助队列。为啥说是键值对存储活用呢？因为这道题可以存储字符的频数或者索引。而且还可以用辅助队列来找第一个满足条件的值，队列挺适合解决这种问题。这些方式的时间复杂度都差不多，就是O(n)，空间也是26个字符的常数空间。
我用hash寸的值也不一样，我用来存标志位。true 表示重复，false 表示不重复。不论 value 存的是啥，都需要遍历两次。

var firstUniqChar = function(s) {
    let hash = {}; // key 是否为重复字符
    for (let c of s) hash[c] = (c in hash);
    for (let i = 0, len = s.length; i < len; i++) {
        if (!hash[s[i]]) return i;
    }
    return -1;
};

187. 重复的DNA序列

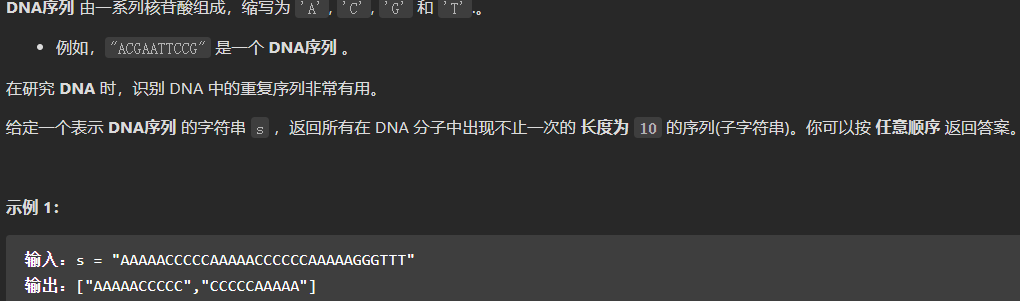
读题干，找到3个点，① 字符只有4个，② 子串的长度必须为10，③ 子串在s中有完全一样的存在视为重复出现。
考察，哈希表、常量语义清晰、滑动窗口、位运算。剩下两种技巧都是高级的了。直接用哈希表就能解出来。
只要遍历s，以10为单位分割子串，用子串为key，出现次数为value。value等于2就添加到结果数组中。时间是O(10N)，空间是O(10N)。

var findRepeatedDnaSequences = function(s) {
    const ans = [], L = 10, LEN = s.length, map = new Map();
    for (let i = 0, n = LEN - L; i <= n; i++) {
        const sub = s.slice(i, i + L);
        if (!map.has(sub)) map.set(sub, 0);
        map.set(sub, map.get(sub) + 1);
        if (map.get(sub) === 2) {
            ans.push(sub);
        }
    }
    return ans;
};

第二种方法，待做。。。。

数学

简单题

7. 整数反转

32位有符号整数x，将整数部分反转。如果反转后整数超过有符号整数的范围（[-2^31, 2^31-1]），就返回0。
考察，越是简单的题越要注重鲁棒。反转方法、负数处理、js 中n次幂的表示。js 中通过移位得到的在32位以内是有效的，但是超过32位就不准了。所以这里的有符号整数边界不能用位运算来表示。我用的是Math.pow()。

var reverse = function(x) {
    let negative = false, sum = 0, rightBound = Math.pow(2, 31) -1 , leftBound = Math.pow(2, 31);
    if (x < 0) {
        negative = true;
        x = -x;
    }
    while(x) {
        sum = sum*10 + x % 10;
        if ((sum > rightBound && !negative) || (sum > leftBound && negative)) return 0;
        x = Math.floor(x/10);
    }
    return negative ? -sum : sum;
};

171. Excel 表列序号

读清题干，其实就是26进制转换为10进制，字符串仅有大写字符，长度为1-7。

var titleToNumber = function(columnTitle) {
    let sum = 0;
    for (let c of columnTitle) {
        let num = (c.charCodeAt() - 'A'.charCodeAt() + 1);
        sum = sum * 26 + num;
    }
    return sum;
};

507. 完美数

完美数就是它和除了它自身以外的所有正因子之和相等，完美数是正整数。判断是否为完美数。还有一种更简洁的解法，用欧拉定理就可以算出来，在[1,10^8]内只有几个数满足这个题目要求。
考察，除了数学理论，也有一些边界情况需要考虑，① sum 初始化为1（需要首先排除 num 为 1 的情况），② 游标需要等于 num 的平方根（num 为 6 的情况，如果平方根的结果取整的话就需要等于，否则就不需要）。

// O(sqrt(num))/O(1)
var checkPerfectNumber = function(num) {
    if (num <= 1) return false;
    let sum = 1, bound = Math.floor(Math.sqrt(num));
    for (let i = 2; i <= bound; i++) {
        if (num % i === 0) {
            sum += i;
            sum += Math.floor(num / i);
        }
    }
    return sum === num;
};
// O(1)/O(1)
var checkPerfectNumber = function(num) {
    return num === 6 || num === 28 || num === 496 || num === 8128 || num === 33550336;
};

中等题

593. 有效的正方形

var validSquare = function(p1, p2, p3, p4) {
    if (
        (p1[0] === p2[0] && p1[1] === p2[1]) ||
        (p1[0] === p3[0] && p1[1] === p3[1]) ||
        (p1[0] === p4[0] && p1[1] === p4[1]) ||
        (p3[0] === p2[0] && p3[1] === p2[1]) ||
        (p4[0] === p2[0] && p4[1] === p2[1]) ||
        (p4[0] === p3[0] && p4[1] === p3[1])
    ) {
        return false;
    }
    return check(p1, p2, p3, p4) || check(p1, p3, p2, p4) || check(p1, p2, p4, p3);
};
var dist = function(p1, p2) {
    return (p2[1]-p1[1])*(p2[1]-p1[1]) + (p2[0]-p1[0])*(p2[0]-p1[0]);
};
var check = function(p1, p2, p3, p4) {
    return dist(p1, p2) > 0 && dist(p1, p2) === dist(p2, p3) && dist(p2, p3) === dist(p3, p4) && dist(p3, p4) === dist(p4, p1) && dist(p1, p3) === dist(p2, p4);
};

双指针

简单题

28. 实现 strStr()

实现还是比较简单，这道题应该可以用 kmp，然而并不记得了。考察，双指针、kmp。
从思考问题的角度出发，应该先列举各种情况，两个字符串都是小写，而且两个字符串的长度可能大于、小于、等于。
双指针思路比较简单，遍历原字符串，当前字符和 needle[0] 相等时，设置两个指针指向haystack[i]和needle[0]，同时比较并且移动。不相等或者 needle 的指针到达 needle.length 时退出循环。

var strStr = function(haystack, needle) {
    let nePot = 0;
    const hLen = haystack.length, nLen = needle.length;
    for (let i =  0; i < hLen; i++) {
        if (haystack[i] === needle[nePot]) {
            let hayPot = i;
            while(nePot < nLen && haystack[hayPot] === needle[nePot]) {nePot++; hayPot++;}
            if (nePot >= nLen) return i;
            nePot = 0;
        }
    }
    return -1;
};

中等题

187. 重复的DNA序列

滑动窗口，yyds。https://www.yuque.com/heyao-uthnw/gr9otg/oku1ck#Xvi9B

字符串

简单题

13. 罗马数字转整数

这道题比较简单，但是写法还真的很简单，但是又能包含所有情况。首先知道的特殊情况，总结一下的话就是当前字符的值小于下一个字符的值就做减法。只需要一个键值对对象保存下罗马字符对应的数值，遍历字符串，做加减法就行了。

var romanToInt = function (s) {
    const hash = { I: 1, V: 5, X: 10, L: 50, C: 100, D: 500, M: 1000 }, len = s.length;
    let sum = 0;
    for (let i = 0; i < len; i++) {
        sum = sum + (hash[s[i]] < hash[s[i+1]] ? -hash[s[i]] : hash[s[i]]);
    }
    return sum;
};

中等题

43. 字符串相乘

第一种解法，乘数与被乘数的每一位进行竖式乘法，再对每次的结果累加。
考察，如何遍历两个字符串、竖式乘法需要根据位数来补零、竖式乘法也要处理仅剩进位的情况、用什么来保存每次竖式乘法的结果（数组？字符串？）。
解题步骤，首先排除其中一个数为0的情况。然后用 for 循环从后往前遍历两个字符串，第一层遍历中定义一个数组，用来保存每一次竖式乘法的结果。补零的操作就可以在定义时进行，使用数组构造函数和 fill。第二层遍历每次结束需要判断 carry，为真则添加进数组中。然后调用 addStrings 进行字符串相加。最终的结果保存在一个字符串变量 ret 里。

var multiply = function(num1, num2) {
    if (num1 === '0' || num2 === '0') return '0';
    let l1 = num1.length - 1, l2 = num2.length - 1, ret = '';
    for (let i = l1; i >= 0; i--) {
        let sub = new Array(l1 - i).fill('0');
        let carry = 0, res;
        for (let j = l2; j >= 0; j--) {
            res = (+num1[i]) * (+num2[j]) + carry;
            sub.push(res % 10);
            carry = Math.floor(res / 10);
        }
        carry && sub.push(carry);
        sub = sub.reverse().join('');
        ret = add(ret, sub);
    }
    return ret;
};
var add = function(num1, num2) {
    let l1 = num1.length - 1,  l2 = num2.length - 1, carry = 0;
    let ret = [];
    while(l1 >= 0 || l2 >= 0 || carry) {
        // 没有转换字符为数字
        let left = l1 < 0 ? 0 : +num1[l1];
        let right = l2 < 0 ? 0 : +num2[l2];
        // 没有控制 l1\l2 移动
        l1--; l2--;
        let sum = left + right + carry;
        ret.push(sum % 10);
        carry = Math.floor(sum / 10);
    }
    return ret.reverse().join('');
}

总逻辑需要两层 for 循环，即 m * n。字符串相加需要 n ^ 2（n 为短的字符串长度）。所以需要时间 O(mn+n^2)。而空间为O(m+n)，不知道咋个分析的。

第二种解法，不是利用竖式乘法的中间结果来做字符串累加，而是一种控制数组下标的方法。提前定义一个 m+n 长的数组 res，然后从后往前遍历进行乘法。规律是这样的 res[i + j + 1] += num1[i] * num2[j]。用 i + j + 1 位来保存相乘的结果，注意是累加的。两层循环乘完之后，再进行单层循环，对 res 里的值进行处理（取余、进位累加）。这里的步骤是 res[i - 1] += res[i] / 10, res[i] = res[i] % 10。这样处理完之后，res 每一个元素都是最终的值了。最后需要判断第一位是否为0，如果不为0，则返回 [0, length-1] 的数字组成的字符串，否则就从 1开始。

var multiply = function(num1, num2) {
    if (num1 === '0' || num2 === '0') return '0';
    let l1 = num1.length - 1, l2 = num2.length - 1, res = new Array(l1 + l2 + 2).fill(0);
    for (let i = l1; i >= 0; i--) {
        for (let j = l2; j >= 0; j--) {
            res[i + j + 1] += (+num1[i]) * (+num2[j]);
        }
    }
    for (let i = l1 + l2 + 1; i > 0; i--) {
        res[i - 1] += Math.floor(res[i] / 10);
        res[i] = res[i] % 10;
    }
    let ret = [];
    for (let i = res[0] === 0 ? 1 : 0, bound = l1 + l2 + 1; i <= bound; i++) {
        ret.push(res[i]);
    }
    return ret.join('');
};

第三种解法，更数学，进行多项式乘法，然后FFT 加速卷积计算，时间 O(clogc)。

树

简单题

面试题 17.12. BiNode

https://leetcode.cn/problems/binode-lcci，题目要求是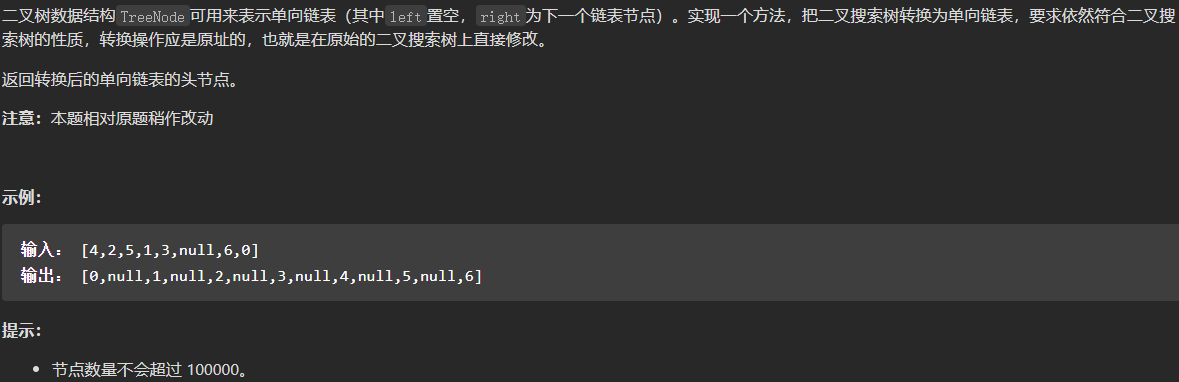

考察知识点，①二叉搜索树；②指针操作；③中序遍历。
BST树的中序遍历就是一个递增的序列。特别需要注意的是指针的操作，和链表反转相同，但不同的是链表反转保存的是下一个节点，这道题需要保存前驱节点。主要思路就是中序遍历的过程中改变前驱节点的指针即可。但是这个过程中需要注意两个问题，①指向相互引用，导致死循环；②构造的单链表的头结点是BST最左下角的节点。

var convertBiNode = function (root) {
    let pre = null, ret = null;
    const inOrderTraverse = (node) => {
        if (node == null) return;
        inOrderTraverse(node.left);
        if (!pre) ret = node;
        node.left = null;
        if (pre) pre.right = node;
        pre = node;
        inOrderTraverse(node.right);
    }
    inOrderTraverse(root);
    return ret;
};

100. 相同的树

很简单，要有一样的结构。题目简单，情况更要考虑全面。考察，树结构、递归。

相同的定义是结构相同，两棵树的结构相同，不仅当前节点要相同，子树也要相同。所以首先检查当前节点。当前节点有4种情况，① 两者都是空节点，② 其中一个为空，③ 都不为空但值不等，④ 都不空且值相等，递归判断左右子树。

var isSameTree = function(p, q) {
    if (p == null && p === q) return true;
    if (p == null || q == null) return false;
    if (p && q && p.val !== q.val) return false;
    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

剑指 Offer 27. 二叉树的镜像

顾名思义，看题干，首先该想到的是改变节点的左右孩子指向。从叶节点到根节点，遍历顺序无所谓。
考察，回溯、修改树节点指向（防止断链）。
中序遍历的时候，终止条件设置为空节点返回当前节点。然后递归左右孩子节点，将返回的节点保存下来，接下来进入回溯部分。将递归左孩子返回的节点赋值给 root.right，root.left 同理。只有这样才能保证不断链。

var mirrorTree = function(root) {
    if (!root) return root;
    let left = mirrorTree(root.right);
    let right = mirrorTree(root.left);
    root.left = left;
    root.right = right;
    return root;
};

中等题

105. 从前序与中序遍历序列构造二叉树

输入两个数组，前序遍历和中序遍历，根据两个数组来建立二叉树。考察，二叉树的构建、递归、迭代、简化查找时间（哈希表-空间换时间）、辅助函数、数组的区间划分。
第一种思路最开始想到，就是用递归，用当前值构造树节点，然后再递归创建左右子树，回溯之后将左右子树的根节点连接上当前节点。每次的根节点就是 preorder[0]，以这个值为准再 inorder 中查找对应的索引。根据这个索引就可以知道如何划分数组了。inorder/preorder 都需要划分为两个子数组。inorder 的新边界就是[instart, index-1]和[index+1, inend]，preorder 的新边界就是[prestart + 1, prestart + index - instart]和[prestart + index - instart + 1, preend]。index-instart 就是新的左边inorder的长度，可以用来计算 preorder 的边界。
重点在于根节点在中序遍历中的索引查找，用 indexOf 方法，这样的时间复杂度势必就上去了，递归加上遍历，O(n^2)。
第二种方法的思路就是简化时间，用哈希表，在构造二叉树之前，保存节点值在inorder的索引。后面构造的时候，查找银锁只需要O(1)的时间，总的时间就被线性拉平了。

var buildTree = function(preorder, inorder) {
    if (!preorder.length) return null;
    const value = preorder[0],
        inorderIndex = inorder.indexOf(value),
        leftPreorder = preorder.slice(1, 1 + inorderIndex),
        rightPreorder = preorder.slice(inorderIndex + 1, preorder.length),
        leftInorder = inorder.slice(0, inorderIndex),
        rightInorder = inorder.slice(inorderIndex + 1, inorder.length);
    let node = new TreeNode(value);
    node.left = buildTree(leftPreorder, leftInorder);
    node.right = buildTree(rightPreorder, rightInorder);
    return node;
};

var buildTree = function(preorder, inorder) {
    const map = new Map(), len = preorder.length;
    for (let i = 0; i < len; i++) {
        map.set(inorder[i], i);
    }
    return doBuildTree(preorder, inorder, 0, len - 1, 0, len - 1, map);
};
var doBuildTree = function(preorder, inorder, preStart, preEnd, inStart, inEnd, map) {
    if (preStart > preEnd) return null;
    let node = new TreeNode(preorder[preStart]);
    const index = map.get(node.val); // 保存的是中序数组中的索引
    node.left = doBuildTree(preorder, inorder, preStart + 1, preStart + index - inStart, inStart, index - 1, map);
    node.right = doBuildTree(preorder, inorder, preStart + index - inStart + 1, preEnd, index + 1, inEnd, map);
    return node;
}

662. 二叉树最大宽度

有思路，但是是错的，总有边界没包括完。

1145. 二叉树着色游戏

不会做。

递归与回溯

简单题

342. 4的幂

判断一个数是不是 4 的幂次方，返回布尔值。读题，考虑问题情况，输入的整数 n 可正可负，负数不可能是 4 的幂次方，直接 false。根据进阶提示，可知“递归”和“迭代”是基础作法，进阶的做法是位运算。
考察，处理正负数的幂次方计算、递归（终结条件、返回值、内部逻辑）、位运算、js 位运算只限32位。
第一种思路，将数取正，利用快速幂，进行拆分，递归直到求解 0 次幂，然后再将结果根据正负取反。需要一个辅助函数。但是需要确定递归的次方，每次从1开始递归时间复杂度必定就会很大，有更聪明一点的做法吗？@TODO
第二种思路，位运算，进行左移位的过程中去判断是否与 n 相等。

var isPowerOfFour = function(n) {
    if (n < 0) return false;
    let tmp = 1, bound = Math.pow(2, 31);
    while(0 < tmp && tmp <= n && tmp < bound) {
        if (tmp === n) return true;
        tmp = tmp << 2;
    }
    return false;
};