排列树- 127-letter combinations of a phone number

Link: https://leetcode.com/problems/letter-combinations-of-a-phone-number/

/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function(digits) {
  let rst = [], local = '';
  if(digits.length === 0) return rst;
  let map = new Map();
  map.set(2, ['a', 'b', 'c']);
  map.set(3, ['d', 'e', 'f']);
  map.set(4, ['g', 'h', 'i']);
  map.set(5, ['j', 'k', 'l']);
  map.set(6, ['m', 'n', 'o']);
  map.set(7, ['p', 'q', 'r', 's']);
  map.set(8, ['t', 'u', 'v']);
  map.set(9, ['w', 'x', 'y', 'z']);
  backtrack(map,rst,local, 0, digits);
  return rst;
};
function backtrack(map, rst, local, index, digits) {
  if(index === digits.length) {
    rst.push(local);
  } else {
    for(let i=0; i<map.get(Number(digits[index])).length; i++) {
      local = local + map.get(Number(digits[index]))[i];
      backtrack(map, rst, local, index+1, digits);
      local = local.substr(0, local.length - 1);
    }
  }
}

算法框架

• 当所给的问题四从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树，例如n个物品的0-1背包问题所相应的解空间树就是一颗子集树。这类子集树通常有2^n个叶节点，其节点总个数为2^(n+1)-1.遍历子集树的任何算法均需2^n的计算时间。

void backtrack(int t)
{
  if(t>n) output(x);
  else
    for(int i=0l i<=1;i++){
      x[t]=i;
      if(Constraint(t)&& Bound(t)) backtrack(t+1);
    }
}

• 当所给问题四是确认n个元素满足某种性质的排列时，相应的解空间树称为排列树，排列树通常有n!个叶节点，因此遍历排列树需要n!的计算时间，旅行售货员问题的解空间树就是一个排列树。

void backtrack(int t)
{
  if(t>n) output(x);
  else
    for(let i=t; i<=n;i++){
      Swap(x[t], x[i]);
      if(Constraint(t)&& Bound(t)) backtrack(t+1);
             // 回溯， 换回去
      Swap(x[t], x[i]);
    }
}

例题讲解

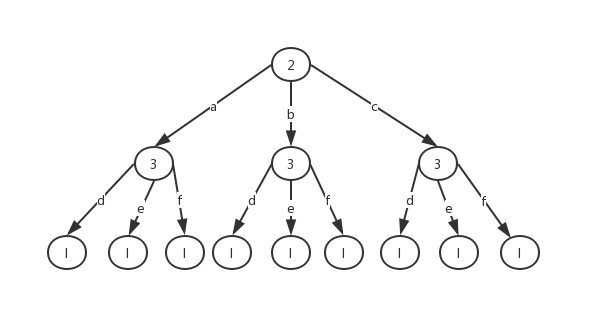
对于“23”来说，其解空间排列树