一、排序
1.排序算法
能够保证相同值元素相对位置的排序算法,叫做稳定排序。
基数排序和归并排序就属于稳定排序,而之前我们学习的快速排序、堆排序都属于非稳定排序。
1.1 快速排序
找到基准值的位置<br /> 将小于基准值的元素放在基准值的前面,将大于基准值的元素放在基准值的后面<br /> 对基准值的左右两侧,递归地进行第一步和第二步<br />基准值的选择决定了时间复杂度<br />基准值每次都是当前区间的中间值时,操作数最少,时间复杂度为 O(nlog_{2}{n})。<br />基准值每次都是当前区间的最小值或最大值时,操作数最多,时间复杂度为 O(n^2)。
// arr : 待排序数组
// l : 待排序区间起始坐标
// r : 待排序区间结束坐标
void quick_sort(int *arr, int l, int r) {
// 递归的边界条件是区间中只有一个元素
// x : 记录从前向后扫描的位置
// y : 记录从后向前扫描的位置
// z : 基准值,选择待排序区间的第一个元素
// while 循环中是 partition 过程
// 每一轮,先从后向前扫,再从前向后扫
if (l >= r) return ;
int x = l, y = r, z = arr[l];
while (x < y) {
while (x < y && arr[y] >= z) --y;
if (x < y) arr[x++] = arr[y];
while (x < y && arr[x] <= z) ++x;
if (x < y) arr[y--] = arr[x];
}
// 将基准值 z 放入其正确位置数组的 x 位
// 其实,此时 x==y,所以写成 arr[y] = z 也行
// 再分别对左右区间,进行快速排序
arr[x] = z;
quick_sort(arr, l, x - 1);
quick_sort(arr, x + 1, r);
return ;
}
1.1.1 快速排序优化
1.1.1.1 单边递归优化
减少函数调用的次数 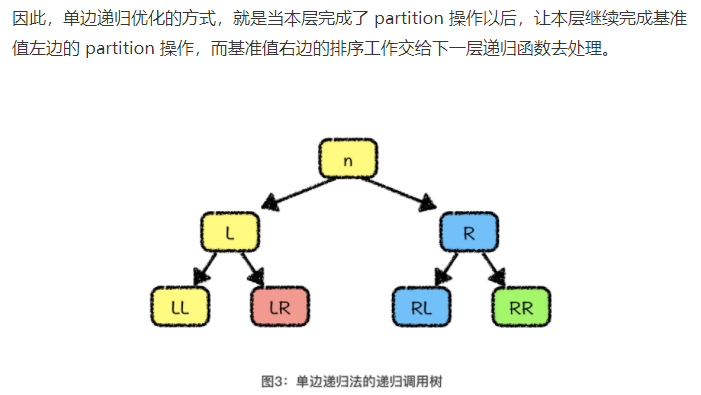
void quick_sort(int *arr, int l, int r) {
while (l < r) {
// 进行一轮 partition 操作
// 获得基准值的位置
int ind = partition(arr, l, r);
// 右侧正常调用递归函数
quick_sort(arr, ind + 1, r);
// 用本层处理左侧的排序
r = ind - 1;
} return ;
}
1.1.1.2 基准值选取优化
为了使快速排序的时间复杂度尽量稳定在 O(nlogn) 而提出来的
三点取中法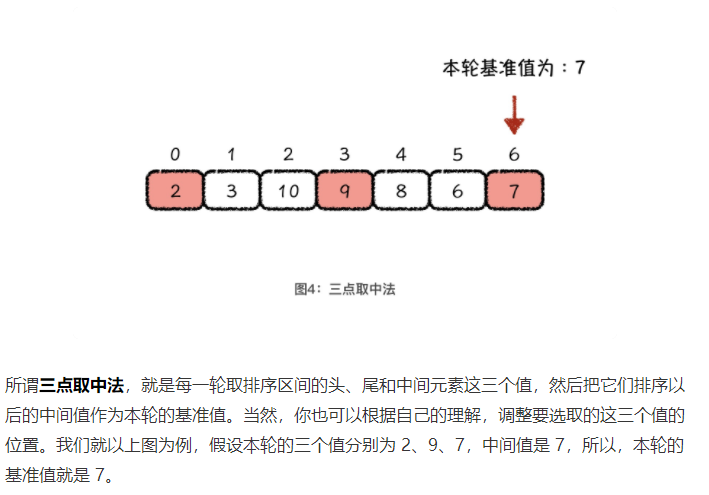
1.1.1.3 partition 操作优化
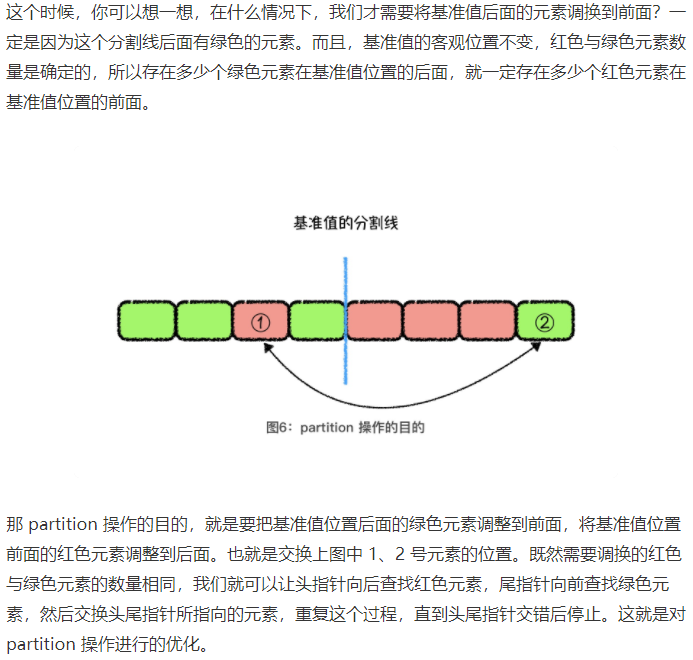
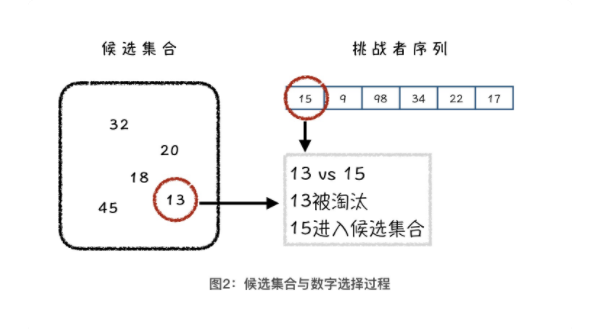
1.2 快速选择
经过一轮 partition 操作以后,我们总能将在当前数组中查找排名第 k 位元素的问题,转化成递归子问题。也就是在基准值的前面查找排名第 k 位的元素,或者在基准值的后面查找排名第 k - ind 位的元素。
快速选择算法的时间复杂度,最好情况是 O(n) ,最坏情况是 O(n^2) ,平均情况是 O(n)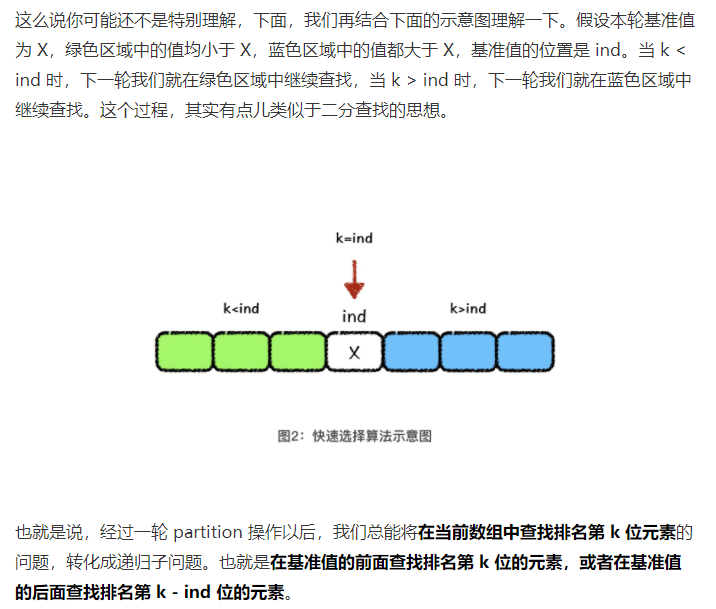
1.3 堆排序
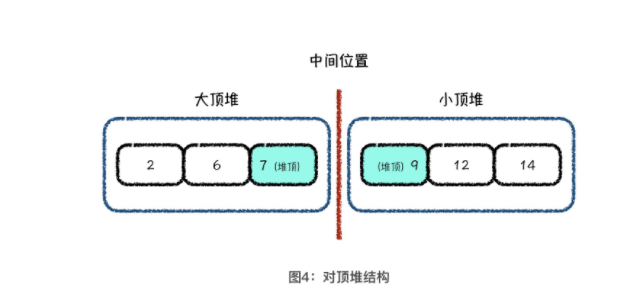
1.3.1 堆是用来维护集合最值的高效数据结构
小顶堆 大顶堆
堆的实际存储结构是数组,这个数组是一段从下标 1 开始的连续存储空间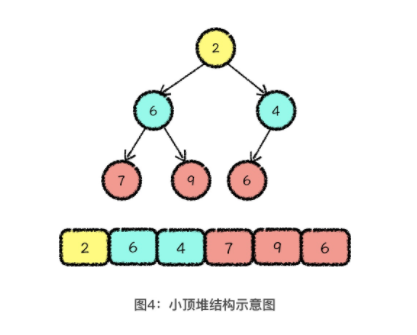
插入操作
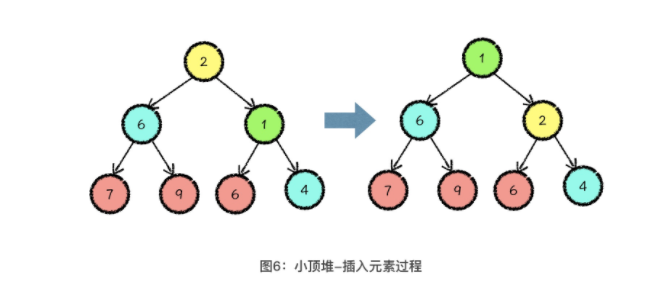
元素放置,放置到整个数组的最后一位,对应到完全二叉树的思维逻辑结构中,就是向树中的最后一层添加了一个新的叶节点 ——> 向上调整,它的原理就是在当前元素值小于其父节点值的时候,交换子节点与父节点值的位置,就这样一直向上调整,直到当前节点大于父节点的值或者调整到了堆顶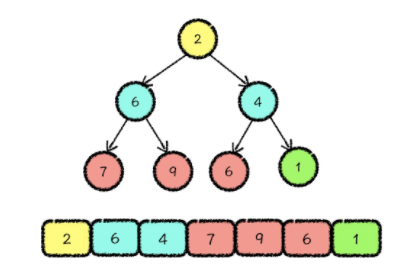
删除操作—-删除最值元素
元素覆盖,用堆的最后一位元素,覆盖掉堆顶元素 ——> 向下调整,从堆顶位置开始,每次从当前元素所在三元组中找到一个最小值,与当前元素交换。交换后,让当前位置的元素继续和下面两个元素比较,如果这个三元组中依然有最小值,那我们就继续向下调整,直到当前元素是三元组中的最小值为止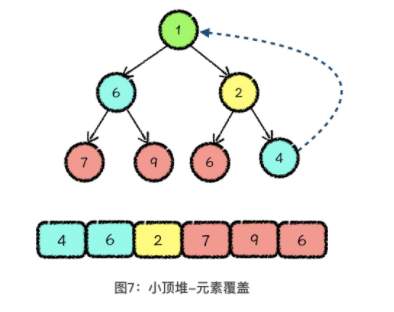
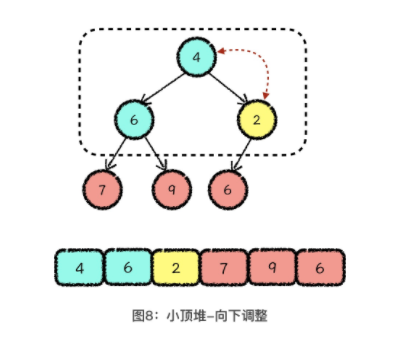
1.3.2 优先队列
如果我们把堆的存储结构看成是一个队列的话,那堆就是一种可以灵活控制元素出队优先级的数据结构,我们管这种结构就叫做优先队列。优先队列当成是一种概念,那它的定义就是一种可以实现根据优先级出队的结构。而堆只是实现优先队列的其中一种方式,当然也是最普遍的方式。
堆排序的流程:
在原数组上建立堆结构 ——>尾插法建堆:用的是向上调整
将堆顶元素与堆末元素进行调换,再对堆顶元素进行向下调整
经过 n 轮操作以后,数组中的元素就有序了
1.3.3 优化
线性建堆法—-用的就是向下调整策略
线性建堆法之所以称为线性,是因为时间复杂度真的为 O(n)
1.3.4 面试题
1.4 线程池
进程 操作系统进行资源分配的最基本单元
线程 操作系统进行运算调度的基本单元
线程池
2.归并排序
2.1 逆序数问题
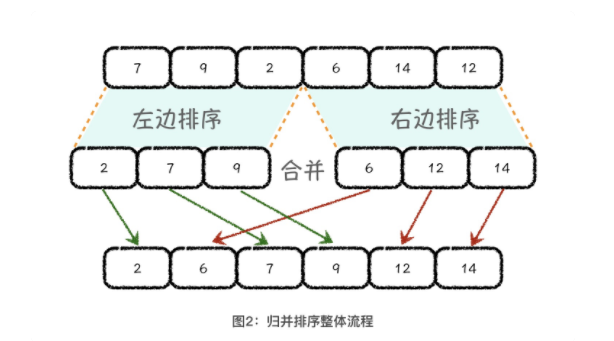
void merge_sort(int *arr, int l, int r) {
if (l == r) return ;
int mid = (l + r) >> 1;
merge_sort(arr, l, mid);
merge_sort(arr, mid + 1, r);
merge(arr, l, mid, r); //关键步骤
return ;
}
2.2 大数据排序问题
多路归并排序 合并过程借用堆 搜索引擎中的倒排索引结构<br />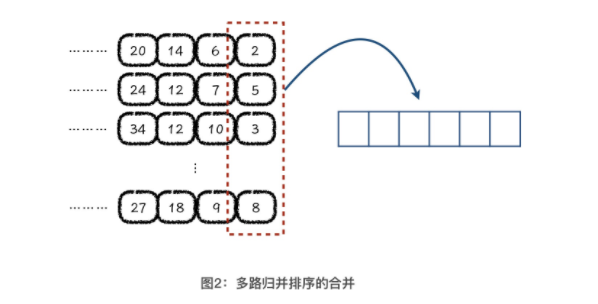
3.有趣的几个排序
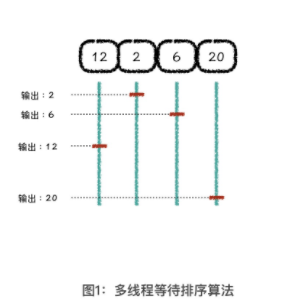
3.1 多线程等待排序
3.2 计数排序
数据具备这种数据范围小,可以有序地映射成数组整型下标的排序问题,采用计数排序算法,是一种既简单又高效的做法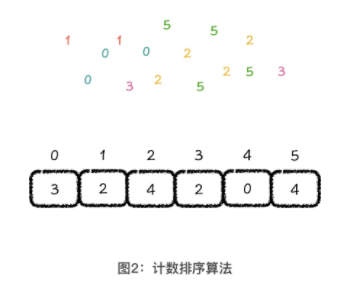
3.3 基数排序
所谓前缀和累加,就是求当前位置之前的所有元素的和值
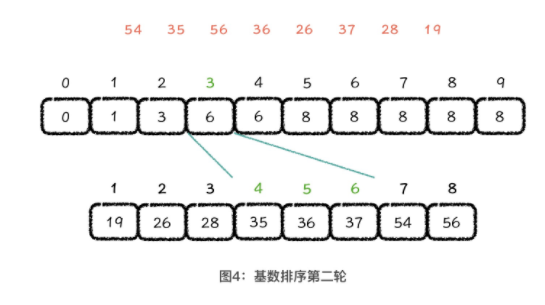
基数排序是从数据的低位到高位进行多轮处理,每一轮以其中一位做为排序的基准,在排序过程中,保证对应位置相同值元素的相对位置保持不变。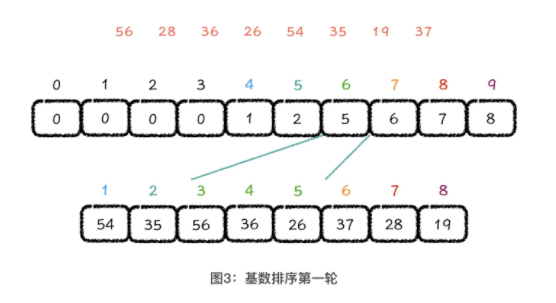
4.面试题
2-sum 问题 存在重复元素 两个数组的交集 合并两个有序的数组
二、查找搜索
1.树
一棵树 T 有一个特定的节点,被称为根节点 root(T)
除根节点之外,其余的节点没切分成 m(m≥0)个不相交的子集 T1,T2,⋯,Tm,每一个子集也都是一棵树,这些子集被称作根节点的子树
树是一种针对集合建模的数据结构。并且,因为树表示了集合的性质,所以树结构有非常好的递推能力
二叉树 树 森林 (无中序遍历)
树—-> 二叉树 左孩子右兄弟 先序遍历是先访问根,再依次访问所有孩子,后序遍历是先访问所有孩子,再访问根
森林—-> 二叉树 我们可以假设森林有一个总体的根,而森林中的所有树都是那个根节点的子树。 先序遍历是先访问第一棵树的根,再访问第一棵树的所有孩子,再访问其他树。后序遍历是先访问第一棵树的所有孩子,再访问第一棵树的根,再访问其他树。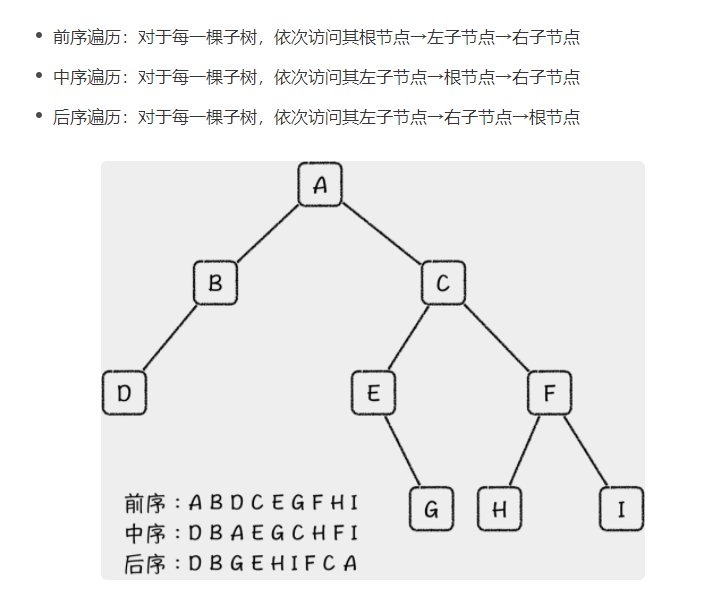
线索化 每一个节点都会存在两条出边,每一个节点的边都会指向它的前驱或者后继,根据遍历顺序的不同,线索化过程也可以分为前序线索化、中序线索化以及后序线索化。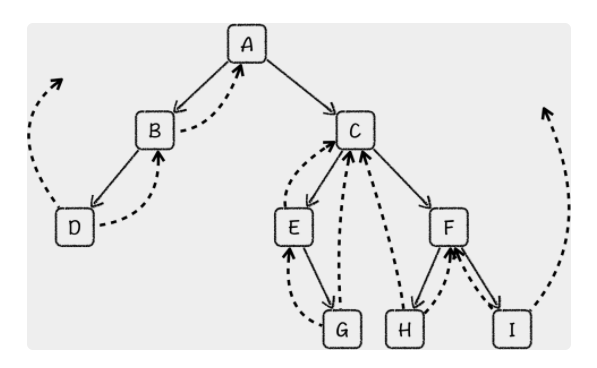
你可以看到,树中只有两个指针是指向空的,分别是最左节点的左线索和最右节点的右线索,每一个节点的左线索指向中序前驱,右线索指向中序后驱。这样,在线索二叉树上的遍历过程中,我们只需要沿着边一直走下去就可以了。
2.二叉排序树(二叉搜索树)
2.1二叉排序树
在二叉排序树中,每一个节点的左子节点都比它小,而右子节点都比它大。
插入 —— 二分查找法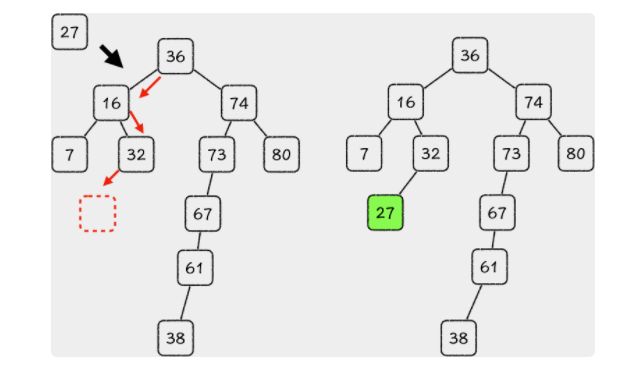
删除 ——找到当前节点中序遍历的后继,使用后继代替被删除节点的位置
3种情况
如果 N 既没有右子节点,也没有左子节点,那我们直接删除 N,释放空间即可。
如果 N 没有右子节点,但是有左子节点,那么我们将左子节点 leftSon(N) 放到 N 的位置上,然后删除 N,释放空间即可。
如果 N 有右子节点,那么从它的右子节点 rightSon(N) 出发,一直向左走,直到走不了为止,然后将最终到达的那个节点 succ(N) 放到 N 的位置,删除掉 N,释放空间即可。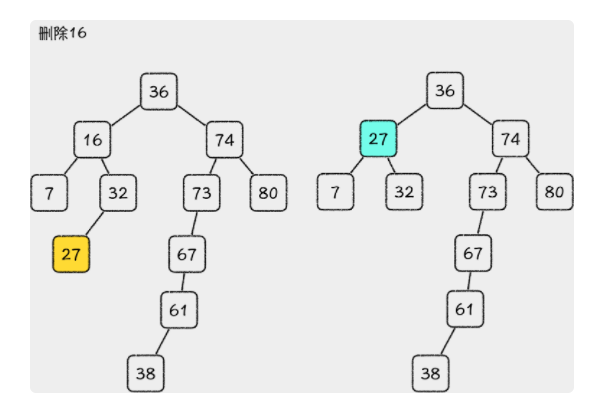
2.2最优二叉排序树
2.3动态规划
状态定义:给问题定义一个带有明确语义信息的数学符号
状态转移方程:我们从递推过程中,总结出来的公式
正确性证明:利用数学归纳法来证明状态转移方程的重要性
程序设计与实现:
3.AVL树(平衡树)
一棵平衡树的左右两棵子树的树高之差不会超过 1。
旋转(Rotate)操作
二叉树的左孩子作为根进行的旋转操作,也被称作是右旋操作(Right Rotate),那与之对称的就是左旋操作(Left Rotate)。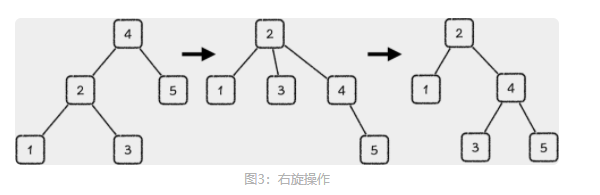
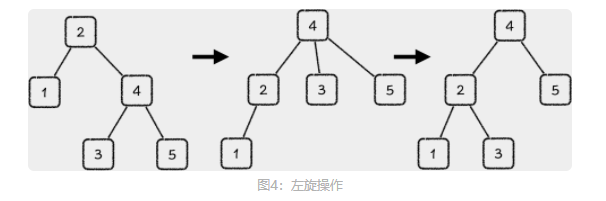
右子树的树高减去左子树的树高,把得到的差叫做平衡因子,在平衡树中,平衡因子只可能有 3 个值:+1,-1 和 0**
4.红黑树
红黑树就是一种每一个节点都被染上黑色或者红色的二叉排序树。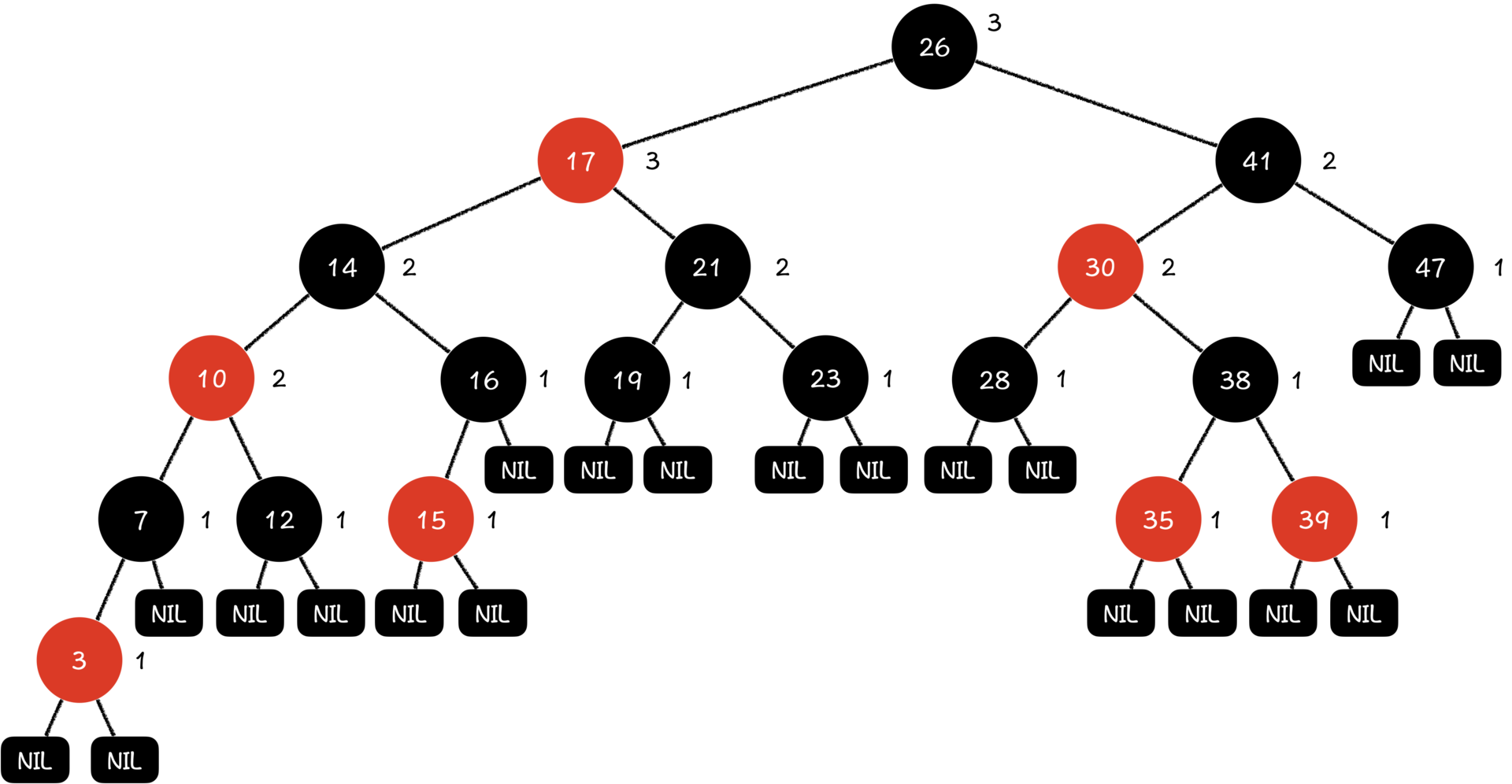
5 个重要性质:
每一个节点的颜色不是红色就是黑色的;
根节点是黑色的;
每一个叶子节点(Nil,最下层节点的空指针孩子)都是黑色的;
如果一个节点是红色的,那它的两个孩子都是黑色的;
对于每一个节点,从它出发到它的后代叶子节点的所有简单路径上,黑色节点的数量都是相同的。
插入操作
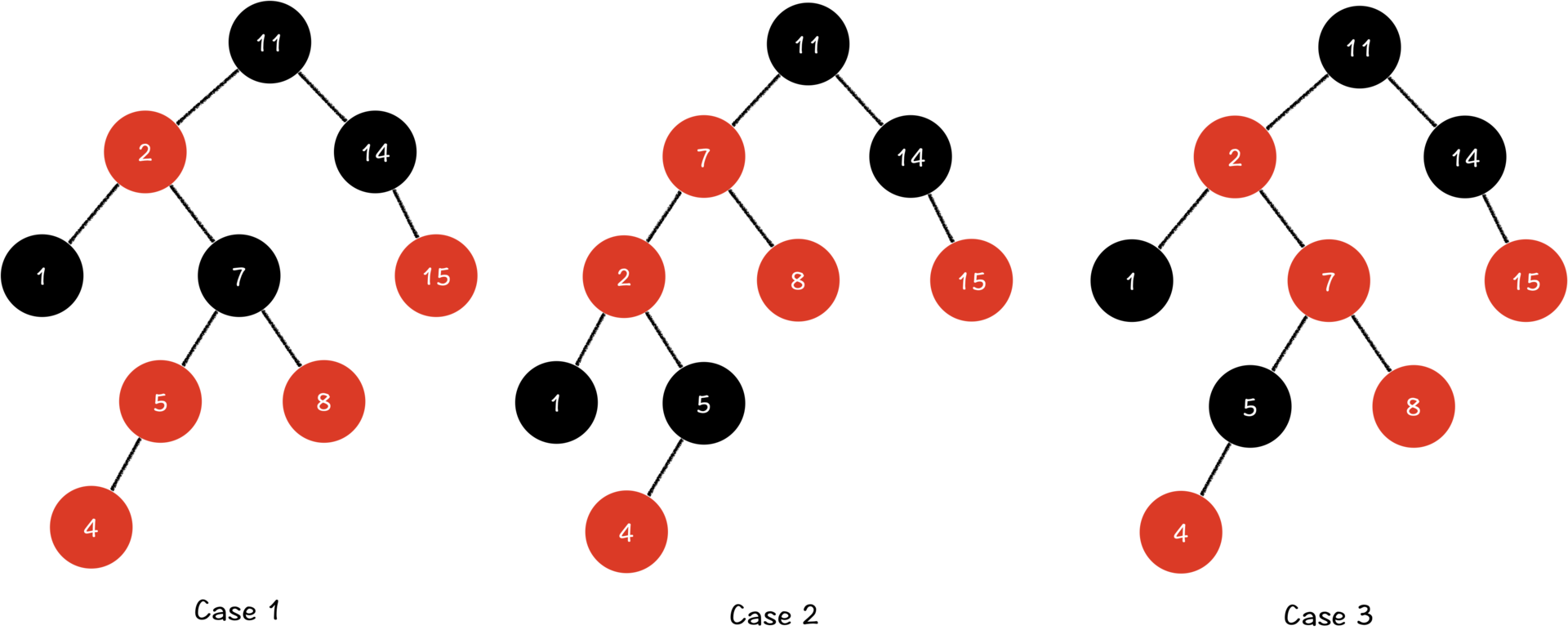
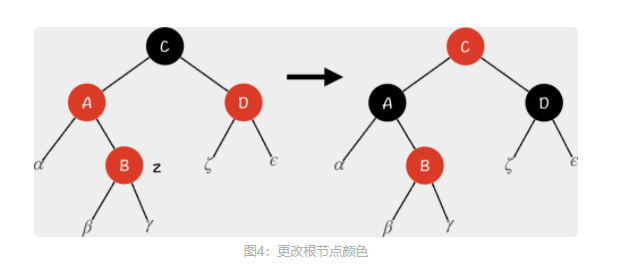
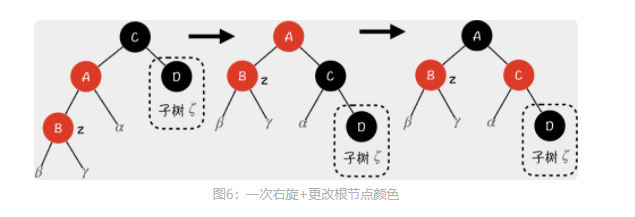
删除操作
Case 1:x 的兄弟节点 w 是黑色节点,w 的两个儿子都是黑色节点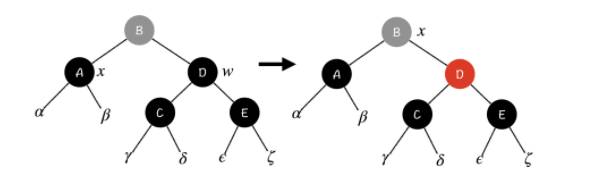
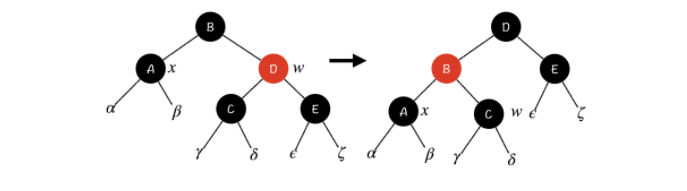
Case 2:x 节点的兄弟节点 w 是黑色节点,w 的右孩子是红色节点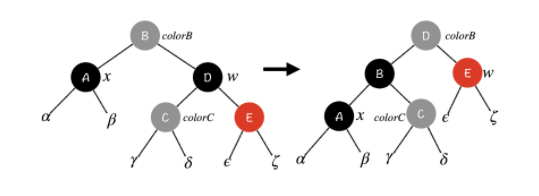
先进行了一次左旋操作,左旋之后又将 D、B 颜色互换,保持了 C 节点所在子树不受影响。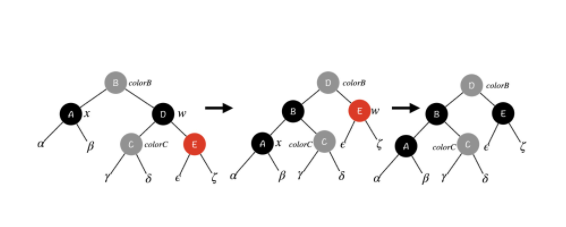
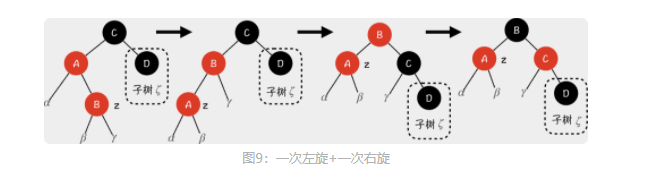
Case 3:x 的兄弟节点 w 是黑色节点,w 的左孩子是红色节点,右孩子是黑色节点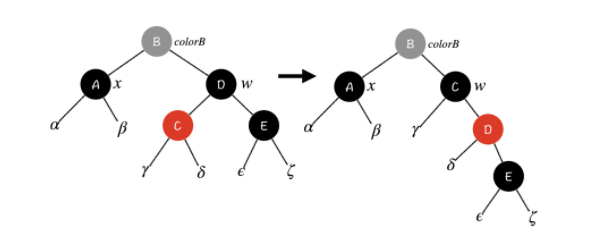
结合上面这张图,我们可以先通过右旋将红色节点变成 w 的右子节点,把它归化到第二种情况中。然后,我们再对 D 节点进行一次右旋。同时,为了保证 γ 子树和 δ 子树的性质,我们将 C 节点和 D 节点的颜色交换一下。这样一来,这种情况就成功归化到了第二种情况中,我们用第二种情况的方法去解决它就好了。
5.哈希表
6.深度优先搜索
状态树—— 树上的节点称作状态,树上的边称作状态转移,状态和状态转移是设计搜索算法的关键。
搜索过程会不断地走到树的深处,所以这个方法叫做深度优先搜索。 所以深度优先搜索要用到栈或递归来实现
剪枝——可以有效帮助我们去掉那些不可能的分支,大幅度地减少运算代价。
八皇后问题
优化
1.改变搜索次序:将分支少的状态尽可能往前放,让前面的状态限制后面的分支,来大幅减少搜索分支;
2.修改状态转移方式,减少无用搜索:如八皇后问题中,我们将格子之间的状态转移转换成为行之间的状态转移,这避免了很多无用的搜索;
3.去掉等效的状态。如组合数问题中,我们已经知道了[1, 2, ]状态和[2, 1, ]状态是一样的,自然不会再进行搜索;
4.去掉不可行的状态,这种剪枝技巧几乎应用到了我们讲过的所有搜索例题中。比如,八皇后问题中,我们对行、列、对角线的限制;再比如,数独问题中我们对行、列、块的限制等等。
7.广度优先搜索
在这个过程中,我们每进行一次操作,都会关注当前状态的所有可能的下一个状态,非常注重广度,所以这个算法就叫做广度优先搜索,也叫做宽度优先搜索,简称就是广搜、宽搜。使用队列来实现这一算法。
松弛操作——检查从当前格子出发到下一个格子是否构成最短路径,并且更新的操作
迷宫问题