一、排序算法
- 1.快速排序
  - 基本思想：
  - 快排示例：
- 2.归并排序
  - 基本思想：
  - 归并示例：
二、查找算法
- 1.二分查找
三、回溯、贪心和动态规划
四、刷题总结
- 1.关于递归反转链表

一、排序算法

1.快速排序

(挖坑排序法经典讲解：https://blog.csdn.net/morewindows/article/details/6684558)

基本思想：

1．先从数列中取出一个数作为基准数。
2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3．再对左右区间重复第二步，直到各区间只有一个数。
挖坑填数+分治法=快速排序算法

快排示例：

以一个数组作为示例，取区间第一个数为基准数。

初始时，i = 0; j = 9; X = a[i] = 72；//X就是取的基准
由于已经将a[0]中的数保存到X中，可以理解成在数组a[0]上挖了个坑，可以将其它数据填充到这来。从j开始向前找一个比X小的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j—;

数组变为：
i = 3; j = 7; X=72
再重复上面的步骤，先从后向前找，再从前向后找。
从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;
从i开始向后找，当i=5时，由于i==j退出。
此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。

数组变为：

可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。

对挖坑填数进行总结
1．i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2．j—由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。
3．i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。
4．再重复执行2，3二步，直到i==j，将基准数填入a[i]中。
照着这个总结很容易实现挖坑填数的代码：

public int AdjustArray(int s[], int l, int r){ //返回调整后基准数的位置
    int i = l, j = r;
    int x = s[i]; //s[l]即s[i]就是第一个坑
    while (i < j){        
        while(i < j && s[j] >= x) // 从右向左找小于x的数来填s[i]
            j--;  
        if(i < j){
            s[i] = s[j]; //将s[j]填到s[i]中，s[j]就形成了一个新的坑
            i++;
        } 
        while(i < j && s[i] < x)// 从左向右找大于或等于x的数来填s[j]
            i++;  
        if(i < j){
            s[j] = s[i]; //将s[i]填到s[j]中，s[i]就形成了一个新的坑
            j--;
        }
    }
    //退出时，i等于j。将x填到这个坑中。
    s[i] = x; 
    return i;
}

再写分治法的代码：

void quick_sort(int s[], int l, int r){
    if (l < r){//l>=r则表示细分到了1个元素
        int i = AdjustArray(s, l, r);//先成挖坑填数法调整s[]
        quick_sort(s, l, i - 1); // 递归调用 
        quick_sort(s, i + 1, r);
    }
}

这样的代码显然不够简洁，对其组合整理下：

//快速排序
private void quickSort(int[] data,int left,int right){
    if(left<right){//细分为每个数组只有一个值的情况了（left==right)
        int i=left;
        int j=right;
        int temp=data[i];//让最左边的为第一个坑，并保留这个位置上的原来的元素
        while (i<j){
            while(i<j && data[j]>=temp) j--;//找到从右往左第一个比坑小的
            if(i<j) {
                data[i]=data[j];
                i++;
            }
            while(i<j && data[i]<=temp) i++;//找到从左往右第一个比坑大的
            if(i<j){
                data[j]=data[i];
                j--;
            }
        }//跳出时为i==j,则把temp放进这个坑里（一个while只是一趟的把一个数组划分为两个分别大和小的数组）
        data[i]=temp;
        quickSort(data, left, i-1);
        quickSort(data, i+1, right);
    }
}

快速排序还有很多改进版本，如随机选择基准数，区间内数据较少时直接用另的方法排序以减小递归深度。

注1，有的书上是以中间的数作为基准数的，要实现这个方便非常方便，直接将中间的数和第一个数进行交换就可以了。

2.归并排序

基本思想：

归并示例：

递归分解+合并数列=归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
首先考虑下如何将将二个有序数列合并。这个非常简单，只要从比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。以下为合并两个有序数列：

//将有序数组a[]和b[]合并到c[]中
void MemeryArray(int a[], int n, int b[], int m, int c[]){
    int i, j, k;
    i = j = k = 0;
    while (i < n && j < m){
        if (a[i] < b[j])
            c[k++] = a[i++];//要么同时移动c和a
        else
            c[k++] = b[j++]; //要么同时移动c和b
    }
    while (i < n)
        c[k++] = a[i++];//将剩余的部分直接接到合并数组中
    while (j < m)
        c[k++] = b[j++];
}

可以看出合并有序数列的效率是比较高的，可以达到O(n)。
解决了上面的合并有序数列问题，再来看归并排序，其的基本思路就是将数组分成二组A，B，如果这二组组内的数据都是有序的，那么就可以很方便的将这二组数据进行排序。如何让这二组组内数据有序了？
可以将A，B组各自再分成二组。依次类推，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列，再合并数列就完成了归并排序。

public static void main (String[] args){
    int a[]={1,5,9,8,9,4,2,34,2,3,56,723,0,34};//测试数据
    int[] temp = new int[a.length];
    mergesort(a, 0, a.length-1, temp);
    for(int num :a )
        System.out.print(num + "  ");
}
//将有二个有序数列a[first...mid]和a[mid+1...last]合并
void mergearray(int a[], int first, int mid, int last, int temp[]){
    int i = first, j = mid + 1;//两个数列的首指针下标
    int m = mid,n = last;s//两个数列的尾指针下标
    int k = 0;//合并后的数列的首指针下标
    while (i <= m && j <= n){
        if (a[i] <= a[j])
            temp[k++] = a[i++];
        else
            temp[k++] = a[j++];
    }
    while (i <= m)
        temp[k++] = a[i++];
    while (j <= n)
        temp[k++] = a[j++];
    for (i = 0; i < k; i++)
        a[first + i] = temp[i];//将排好序的数列替换掉原始数组的内容
}
//递归和合并数列
void mergesort(int a[], int first, int last, int temp[]){
    if (first < last){//递归的终止条件：就是分出来的小组只有一个数据就停止
        int mid = (first + last) / 2;
        mergesort(a, first, mid, temp);    //不断递归左边，最终得到左边有序
        mergesort(a, mid + 1, last, temp); //不断递归左边，最终得到右边有序
        if(a[mid]<a[mid+1]) return;//如果已经是有序，则不需要继续合并
        mergearray(a, first, mid, last, temp); //最后再将二个有序数列合并
    }
    //然后继续向上合并
}

归并排序的效率是比较高的，设数列长为N，将数列分开成小数列一共要logN步，每步都是一个合并有序数列的过程，时间复杂度可以记为O(N)，故一共为O(NlogN)。因为归并排序每次都是在相邻的数据中进行操作，所以归并排序在O(NlogN)的几种排序方法（快速排序，归并排序，希尔排序，堆排序）也是效率比较高的。
注：有的书上是在mergearray()合并有序数列时分配临时数组，但是过多的new操作会非常费时。因此作了下小小的变化。只在MergeSort()中new一个临时数组。后面的操作都共用这一个临时数组。

二、查找算法

1.二分查找

1.1经典二分问题

基本思想：

二分查找是一种基于比较目标值和数组中间元素的教科书式算法。针对元素有序的（升序）整型数组

如果目标值等于中间元素，则找到目标值。
如果目标值较小，证明目标值小于中间元素及右边的元素，继续在左侧搜索。
如果目标值较大，证明目标值大于中间元素及左边的元素，继续在右侧搜索。

算法代码描述：
初始化指针 left = 0, right = n - 1。
当 left <= right：比较中间元素 nums[pivot] 和目标值 target 。
如果 target = nums[pivot]，返回 pivot。
如果 target < nums[pivot]，则在左侧继续搜索 right = pivot - 1。
如果 target > nums[pivot]，则在右侧继续搜索 left = pivot + 1。

经典二分问题：
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target 。写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。【存在就返回存在的那个下标】

java代码实现:
```
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;//分别准备好左右端点
while (left <= right) {//循环二分
 int pivot = left + (right - left) / 2;//取中点
 if (nums[pivot] == target) return pivot;//找到答案并返回
 if (target < nums[pivot]) right = pivot - 1;//向左继续找
 else left = pivot + 1;//向右继续找
}
return -1;//未找到，返回-1
}
}
```
1.2 基础二分小变形1
将目标数插入到第一个比目标值大的数左边
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。你可以假设数组中无重复元素。
思路：我们注意，这一题和上一题的区别在于，这一题并不存在‘没找到’这种情况，因为要插入到”第一个比目标值大的数“的左边，返回这样一个插入位置，你不可能”找不到“，不可返回-1。
事实上，我们的目标也再不是找到一个相同的数字，而是找到第一个比目标值大的数，也就是插入位置。
代码的内部逻辑是”一路找到最后，返回的一定是答案“，而上段代码的逻辑是”边找边判断，找到最后还没有找到，就返回-1“。

代码实现
```
public class Solution {
public int searchInsert(int[] nums, int target) {
   int left = 0;
   while (left <= right) {
       int mid = (left + right) / 2;
       if (nums[mid] < target) {//此处注意不需要等号，加等号是加在最右边，不加等号是加在最左边
           left = mid + 1;
       } else {
           right = mid - 1;
       }
   }
   return left;
}
}
```
提醒：所以，如果你是一个想注重细节，做到写二分代码不出错，那么你就需要关心最后返回值，while结束条件，while内部是否加判断等等这些细节了。

1.3基础二分小变形2

查找某个目标值的边界
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(logn) 级别。
如果数组中不存在目标值，返回 [-1, -1]。
示例 1:输入: nums = [5,7,7,8,8,10], target = 8输出: [3,4]
示例 2:输入: nums = [5,7,7,8,8,10], target = 6输出: [-1,-1]

思路：两个二分，稍微改一下，就可以找到第一个target或最后一个target；

本元素和前面一个元素不相等，才代表找到了最左边的目标元素。
本元素和后面一个元素不相等，才代表找到了最右边的目标元素。

代码实现
```
class Solution {
  public int[] searchRange(int[] nums, int target) {
      int[] ans=new int[2];
      ans[0]=searchRangeLeft(nums,target);
      ans[1]=searchRangeRight(nums,target);
      return ans;
  }
  public int searchRangeLeft(int[] nums, int target) {
      int left=0;
      int right=nums.length-1;
      while(left<=right){
          int mid=(left+right)/2;
          if(nums[mid]>target){//小于中间值，往左边查找
              right=mid-1;
          }else if(nums[mid]<target){//大于中间值，往右边查找
              left=mid+1;
          }else if(mid==0 || nums[mid-1]!=target){//mid==0是为了防止mid-1越界,同时也是右边界
              //中间值等于目标值，前一个值不等于目标值，查找到了最左边 或者 已经查找到最左边
              return mid;
          }else{
              right=mid-1;//中间值等于目标值，前一个值还等于目标值，继续向左缩小目标范围
          }
      }
      return -1;
  }
  public int searchRangeRight(int[] nums, int target) {
      int left=0;
      int right=nums.length-1;
      while(left<=right){
          int mid=(left+right)/2;
          if(nums[mid]>target){
              right=mid-1;
          }else if(nums[mid]<target){
              left=mid+1;
          }else if(mid==nums.length-1 || nums[mid+1]!=target){
              //mid==len-1是为了防止mid+1越界，同时也是左边界
              return mid;
          }else{
              left=mid+1;
          }
      }
      return -1;
  }
}
```
1.4泛化二分的概念

与有序无序无关
简单来说，我百度百科对二分的定义就是在顺序存储结构（数组）有序的情况下进行二分查找。
从第四节开始，我们介绍的就不是传统意义上的二分查找了，不局限于”有序“，甚至不局限于线性结构，while循环里判断向左还是向右搜索的条件也不会这么单一，而更可能是这样：
while (范围没有缩小为0) {
if (满足某种条件) {
排除一半答案
} else {
排除另一半答案
}
}
我们的思想是：只要可以通过正确逻辑，用二分思想正确的缩小查找范围，都称之为二分。
下面就来体会一下什么是二分思想：
我们正在玩一个猜数字游戏。游戏规则如下：我从 1 到 n 选择一个数字。你需要猜我选择了哪个数字。每次你猜错了，我会告诉你这个数字是大了还是小了。
你调用一个预先定义好的接口 guess(int num)，它会返回 3 个可能的结果（-1，1 或 0）：
-1 : 我的数字比较小
1 : 我的数字比较大
0 : 恭喜！你猜对了！
示例 :
输入: n = 10, pick = 6输出: 6

代码实现
```
public class Solution extends GuessGame {
  public int guessNumber(int n) {
      int low = 1;
      int high = n;
      while (low <= high) {
          int mid = low + (high - low) / 2;
          int res = guess(mid);
          if (res == 0)
              return mid;
          else if (res < 0)
              high = mid - 1;
          else
              low = mid + 1;
      }
      return -1;
  }
}
```
这就是把条件抽象成一个接口，完全脱离了线性数据结构，更和有序无序没关系，只是二分的思想。

1.5在线性结构上二分的题目积累

例1：找峰值元素
峰值元素是指其值大于左右相邻值的元素。给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。
示例 1:输入: nums = [1,2,3,1]输出: 2
解释: 3 是峰值元素，你的函数应该返回其索引 2。
示例 2:输入: nums = [1,2,1,3,5,6,4]输出: 1 或 5
解释: 你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5，其峰值元素为 6。
说明:你的解法应该是 O(logN) 时间复杂度的。
思路：可以用二分的要求：线性表能够根据中间元素的特点推测它两侧元素的性质，以达到缩减问题规模的效果即可，不一定非要有序。具体到本题来说，我们如何做到搜索到任何一个“峰值”呢？请看图：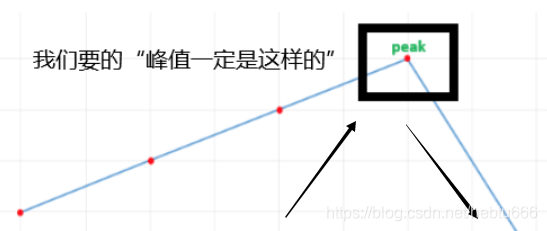

要先有上升的趋势，后有下降的趋势。更通俗一点就是说，要保证前一个数字比峰值小，后一个数字比峰值大，我们只要每次搜索都满足这个条件，搜到最后就一定可以找到某个峰值，因为从递增到递减，肯定是因为中间有峰值的存在所导致的。

我们看中点，如果中点向右有递增趋势，我们就继续搜索右边：

反之，有向左递增的趋势，我们就搜左边：

实现代码
```
public class Solution {
  public int findPeakElement(int[] nums) {
      int l = 0, r = nums.length - 1;
      while (l < r) {
          int mid = (l + r) / 2;
          if (nums[mid] > nums[mid + 1])
              r = mid;
          else
              l = mid + 1;
      }
      return l;//最后缩小到l==r时，就找到了峰值
  }
}
```
我们发现，这个题目的代码逻辑就是第二节的”一路找到最后，返回的一定是答案“，不同于最基础的二分”边找边判断，找到最后还没有找到，就返回-1“。我们是缩小范围到最后，找到了答案l。

例2：找原有序旋转数组的旋转后最小元素
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能为 [4,5,6,7,0,1,2] )。请找出其中最小的元素。你可以假设数组中不存在重复元素。
示例 1:
输入: [3,4,5,1,2]输出: 1
示例 2:
输入: [4,5,6,7,0,1,2]输出: 0
分析：
如果数组没有翻转，即 nums[left] <= nums[right]，则 nums[left] 就是最小值，直接返回。
如果数组翻转，需要找到数组中第二部分的第一个元素：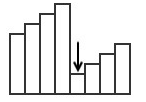
。
下面讨论数组翻转的情况下，如何收缩区间以找到这个元素：
若 nums[left] <= nums[mid]，说明区间 [left,mid] 连续递增，则最小元素一定不在这个区间里，可以直接排除。因此，令 left = mid+1，在 [mid+1,right] 继续查找。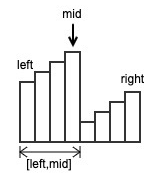

否则，说明区间 [left,mid] 不连续，则最小元素一定在这个区间里。因此，令 right = mid，在 [left,mid] 继续查找[left,right] 表示当前搜索的区间。
注意 right 更新时会被设为 mid 而不是 mid-1，因为 mid 无法被排除。
代码实现
```
class Solution {
  public int findMin(int[] nums) {
      if(nums.length==1) return nums[0];
      if(nums[0]<nums[nums.length-1]) return nums[0];
      int left=0;
      int right=nums.length-1;
      int mid=0;
      while(left<right){
          mid=(left+right)/2;
          if(nums[mid]>=nums[0]){
              left=mid+1;
          }else{
              right=mid;
          }
      }
      return nums[right];//最后缩小到了left==right，就找到了最小值
  }
}
```
例3：找原有序旋转数组是否存在某个目标值，并返回其索引
其它条件和例2一样，例3要搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。
思路：先通过例2的方法找到分割点，再对左右某一边进行二分即可。
解答：可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例[4,5,6,7,0,1,2]来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：
如果 [l, mid] 是有序数组，且 target 的大小满足 [nums[l],nums[mid-1]]，则我们应该将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
如果 [mid, r] 是有序数组，且 target 的大小满足 [nums[mid+1],nums[r]]，则我们应该将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。

代码实现

public static int search(int[] nums, int target) {
    int n = nums.length;
    if (n == 0) {
        return -1;
    }
    if (n == 1) {
        return nums[0] == target ? 0 : -1;
    }
    int l = 0, r = n - 1;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (nums[mid] == target) {//相等的时候返回
            return mid;
        }
        if (nums[0] <= nums[mid]) {//
            if (nums[0] <= target && target < nums[mid]) {//
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        } else {//
            if (nums[mid] < target && target <= nums[n - 1]) {//
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
    }
    return -1;
}

1.6二维数组的二分查找

判断 m x n 矩阵中，是否存在一个目标值

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例 1:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 3
输出: true
示例 2:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 13
输出: false
仔细观察我们发现，其实这个二维数组整体就是有序的，所以当成一维数组二分查找即可，但是要注意二维数组的操作，需要一点功底。
代码实现

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0) {
            return false;
        }
        int row = matrix.length;
        int col = matrix[0].length;
        int start = 0;
        int end = row * col - 1;
        while (start <= end) {
            int mid = start + (end - start) / 2;//正规的二分写法，避免溢出
            if (matrix[mid / col][mid % col] == target)
                return true;
            else if (matrix[mid / col][mid % col] > target)
                end = mid - 1;
            else 
                start = mid + 1;
        }
        return false;
    }
}

1.7二叉树上二分的题目积累

我们刚才学会了一些一维二维数组的二分操作，下面我们再去其它数据结构试试看，继续养成二分的思想。

例1：先看一道简单的在二叉树上查找值。

给定一个不为空的二叉搜索树和一个目标值 target，请在该二叉搜索树中找到最接近目标值 target 的数值。
注意：给定的目标值 target 是一个浮点数，题目保证在该二叉搜索树中只会存在一个最接近目标值的数。
示例：
输入: root = [4,2,5,1,3]，目标值 target = 3.714286
4
/ \
2 5
/ \
1 3
输出: 4
思路：二分，当前节点比target大就往左边搜（因为右边的差距更大），当前节点比target小就往右搜（因为左边的差距更大）。
补充：二叉查找树它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树。
代码实现

public class MyTest {
    public static void main(String[] args) {
        TreeNode node1=new TreeNode(4);
        TreeNode node2=new TreeNode(2);
        node1.left=node2;
        node1.right=new TreeNode(5);
        node2.left=new TreeNode(1);
        node2.right=new TreeNode(3);
        int closest=closestSearch(node1,2.714286);
        System.out.println(closest);
    }
    private static int closestSearch(TreeNode root,double target){
        int val=root.val;
        int closest=root.val;//closest最近的
        while(root!=null){
            val=root.val;
            closest=Math.abs(val-target)<Math.abs(closest-target)?val:closest;//上次的差值和这次的比较
            root=root.val>target?root.left:root.right;
        }
        return closest;
    }
}
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x){
        val = x;
    }
}

例2：给出一个完全二叉树，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。
示例:
输入:
1
/ \
2 3
/ \ /
4 5 6
输出: 6
思路：如果不考虑最后一层，节点数完全可以算出来，每一层分别为1，2，4，8….你会发现是2的n次方，那么总和也很好求，所以问题就在于如何知道最后一层有多少节点，换句话说，最后一层的最右边的那个节点在哪里？我们需要二分搜索。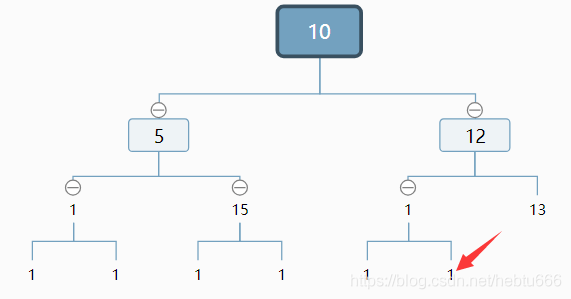
我的算法学习记录 - 图10
目标：找箭头指向的结点。
我们采用二分法：
1）找到右子树的最左结点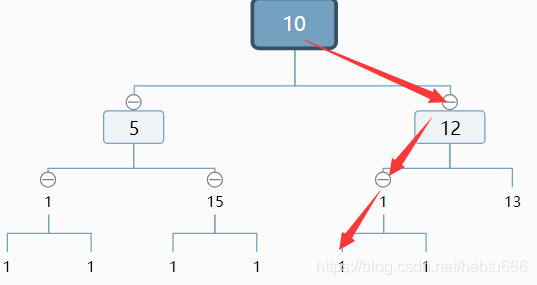
我的算法学习记录 - 图11

我们知道总深度为4，如果右子树深度为3，说明我的算法学习记录 - 图12 图中最后的1是存在的（说明最后一行最右结点一定来自右子树），否则，如果我们修改一下如下图：
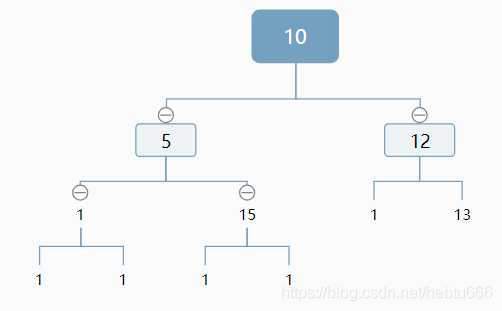
我的算法学习记录 - 图13
右子树深度为2！=4-1，不存在最后一行的结点。（说明最后一行最右结点一定来自左子树）.
2）判断之后，如果是这种情况，我们排除了左子树，计算排除的结点个数，并对右子树（如图2）做相同的处理。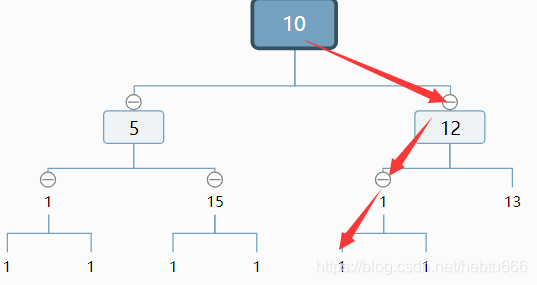
我的算法学习记录 - 图14
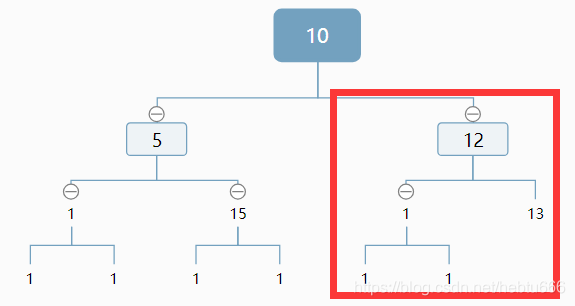
我的算法学习记录 - 图15

更新结点数（未被框起的部分，满二叉树公式+1）+1是根结点
3）对方框内重复此过程。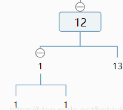
我的算法学习记录 - 图16
我们继续看右子树，发现右子树深度为1！=3-1.
说明最深层最右结点来自于左子树。所以对左子树重复上述过程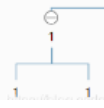
我的算法学习记录 - 图17
我们发现，右子树深度=1=2（整棵树深度）-1，说明最深层最右结点来自于右子树，所以对右子树重复此过程。我的算法学习记录 - 图18 最终找到它。
代码实现

public class TestStaticClass {
    public static class Node {
        public int value;
        public Node left;
        public Node right;
        public Node(int data) {
            this.value = data;
        }
    }
    //返回结点个数
    public static int nodeNum(Node head) {
        if (head == null) {
            return 0;
        }
        return bs(head, 1, mostLeftLevel(head, 1));
    }
    //返回根为node，当前层数为l，总深度为h的结点个数
    public static int bs(Node node, int l, int h) {
        if (l == h) {
            return 1;//到达最后一层
        }
        if (mostLeftLevel(node.right, l + 1) == h) { //右子树最深一行最左不为空
            return (1 << (h - l)) + bs(node.right, l + 1, h);    //右bs+左子树结点个数
        } else {                                                 //右子树最深一行最左为空
            return (1 << (h - l - 1)) + bs(node.left, l + 1, h);//左bs+右子树结点个数
        }
    }
    //计算树的高度
    public static int mostLeftLevel(Node node, int level) {
        while (node != null) {
            level++;
            node = node.left;
        }
        return level - 1;
    }
    public static void main(String[] args) {
        Node head = new Node(1);
        head.left = new Node(2);
        head.right = new Node(3);
        head.left.left = new Node(4);
        head.left.right = new Node(5);
        head.right.left = new Node(6);
        System.out.println(nodeNum(head));
    }
}

补充：
1.满二叉树公式为 (2^k) -1 【k是树的层数】
2.关于使用static关键字修饰类：
java里面static一般用来修饰成员变量或函数。但有一种特殊用法是用static修饰内部类，普通类是不允许声明为静态的，只有内部类才可以。被static修饰的内部类可以直接作为一个普通类来使用，而不需实例一个外部类（见如下代码）：需要注意的是当一个内部类没有使用static修饰的时候，是不能直接使用内部类创建对象，须要先使用外部类对象点new内部类对象及(外部类对象.new 内部类（）)

1、被static修饰的内部类可以直接作为一个普通类来使用，而不需实例一个外部类
class OuterClass {
    public static class InnerClass{
        public InnerClass(){
            System.out.println("============= 我是一个内部类'InnerClass' =============");
           }
       public void test(){
       }
   }
 }
 public class TestStaticClass {
    public static void main(String[] args) {
         new OuterClass.InnerClass();// 不需要new一个InnerClas
          new OuterClass.InnerClass().test();
    }
}
2、如果没有用static修饰InterClass，则只能按如下方式调用：需要先new 一个外部类实例
        OuterClass oc = new OuterClass(); 在使用外部类实例点内部类实例
        oc.new InnerClass();
class OuterClass {
    public class InnerClass{
        public InnerClass(){
            System.out.println("============= 我是一个内部类'InnerClass' =============");
        }
        public void test(){
           }
    }
}
public class TestStaticClass {
    public static void main(String[] args) {
        new OuterClass().new InnerClass();// OutClass需要先生成一个实例，然后再new一个InnerClass();
        new OuterClass().new InnerClass().test();
    }
}

1..8数学中的二分

实现 int sqrt(int x) 函数。计算并返回 x 的平方根，其中 x 是非负整数。由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。
示例 1:
输入: 4输出: 2
示例 2:
输入: 8输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。
思路依旧是二分，格式和上文都一样。
代码实现

public class MyTest {
    public static void main(String[] args) {
        int i = mySqrt(8);
        System.out.println(i);
    }
    public static int mySqrt(int x) {
        long left = 0;
        long right = Integer.MAX_VALUE;// MAX_VALUE=0x7fffffff;
        while (left < right) {
            // >>>表示无符号右移，也叫逻辑右移，即若该数为正，则高位补0，而若该数为负数，则右移后高位仍补0
            long mid = (left + right + 1) >>> 1;
            long square = mid * mid;
            if (square > x) {
                right = mid - 1;
            } else {
                left = mid;
            }
        }
        return (int) left;//left==right时跳出循环
    }
}

1.9最大化或最小化问题

如果在求解最大最小问题中，能比较简单的判断某个解是否满足条件（这里的简单一般指的是o(n)及以下，视具体数据范围而定），使用二分搜索答案就能很好的解决问题。
题目链接：http://poj.org/problem?id=1064
题目大意：有n条绳子，长度分别为L[i]。如果从他们中切割出k条长度相同的绳子的话，这k条绳子每条最长能有多长？（答案保留小数点后两位，规定1单位长度的绳子最多可以切割成100份）。
思路：二分搜索答案，每条最短0，最大设置一个较大的数，然后开始二分答案并依次判断，判断也很简单，判断每个绳子的长度整除答案的累加和是不是大于k就好了。
代码实现
补充：有n个牛栏，选m个放进牛，相当于一条线段上有 n 个点，选取 m 个点，使得相邻点之间的最小距离值最大
思路：和上一道题类似，二分答案，判断答案也很简单，贪心即可，遍历，遇到大于枚举的距离就放一只牛，看最后能不能放得下。
代码实现

三、回溯、贪心和动态规划

回溯、贪心和动态规划三类算法思想是层层递进，环环相扣的，如果想学习好的话，就应该放在一起系统的学习，否则，你很难学会他们
如果你能系统的完成下面的 36 道算法面试题的话，那么对于回溯、贪心和动态规划的问题，就会很容易的解答了：
回溯算法思想

leetcode 112 号算法题：路径总和
leetcode 113 号算法题：路径总和 II
leetcode 46 号算法题：全排列
leetcode 47 号算法题：全排列 II
leetcode 77 号算法题：组合
leetcode 39 号算法题：组合总和
leetcode 40 号算法题：组合总和 Ⅱ
leetcode 216 号算法题：组合总和 Ⅲ
leetcode 78 号算法题：子集
leetcode 90 号算法题：子集Ⅱ
leetcode 17 号算法题：电话号码的字母组合
leetcode 93 号算法题：复原 IP 地址
leetcode 22 号算法题：括号生成
leetcode 51 号算法题：N 皇后
leetcode 37 号算法题：数独问题

贪心算法思想

leetcode 455 号算法题：分发饼干
leetcode 322 号算法题：零钱兑换
leetcode 45 号算法题：跳跃游戏 Ⅱ
leetcode 1578 号算法题：避免重复字母的最小删除成本
leetcode 402 号算法题：移掉K位数字

动态规划算法思想

leetcode 509 号算法题：斐波那契数
leetcode 322 号算法题：零钱兑换
leetcode 64 号算法题：最小路径和
leetcode 53 号算法题：最大子数组之和
leetcode 647 号算法题：回文子串
leetcode 5 号算法题：最长回文串
leetcode 131 号算法题：分割回文串
leetcode 516 号算法题：最长回文子序列
leetcode 300 号算法题：最长上升子序列
leetcode 1143 号算法题：最长公共子序列
leetcode 72 号算法题：编辑距离
leetcode 44 号算法题：通配符匹配
leetcode 10 号算法题：正则表达式匹配
leetcode 486 号算法题：预测赢家
leetcode 877 号算法题：石子游戏
0-1 背包问题

你可以按照上面的顺序来刷这些题目，注意，一定要按照回溯，然后贪心，最后才动态规划的顺序来刷题，我相信你能系统的学会回溯、贪心和动态规划
题解

回溯算法思想

leetcode 112 号算法题：路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点是指没有子节点的节点。
示例 1：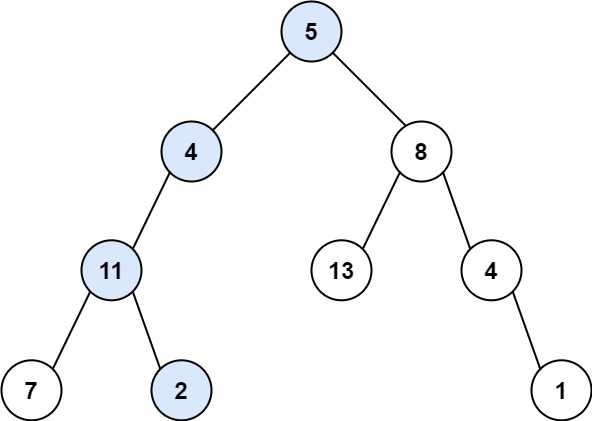
我的算法学习记录 - 图19
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true

//深度优先搜索
class Solution {
    //只有深度遍历的每一层都返回true才会最终返回true(从最深处逐级往上)
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null)//如果这个成立，说明是像题干中的4的左节点一样的节点，4并不是叶子节点，防止没到叶子节点但累计和到了目标和的情况
            return false;
        if(root.left==null&&root.right==null)//只有是叶子节点
            return targetSum==root.val;
        return hasPathSum(root.left,targetSum-root.val)||
                hasPathSum(root.right,targetSum-root.val);
    }
}
或
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        return dfs(root, targetSum, 0);
    }
    private boolean dfs(TreeNode node,int targetSum,int nodeValSum){
        if(node==null)
            return false;
        if(node.left==null&&node.right==null)
            return (nodeValSum+node.val)==targetSum;
        return dfs(node.left,targetSum,nodeValSum+node.val)||dfs(node.right,targetSum,nodeValSum+node.val);
    }
}
或
//广度优先搜索
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null) return false;
        LinkedList<TreeNode> nodeQue=new LinkedList<>();
        LinkedList<Integer> valQue=new LinkedList<>();
        nodeQue.addLast(root);
        valQue.addLast(root.val);
        while (!nodeQue.isEmpty()){
            TreeNode node=nodeQue.pollFirst();
            Integer value = valQue.pollFirst();
            if(node.left==null&&node.right==null){//才是叶子节点
                if(value==targetSum)
                    return true;
                continue;//当前节点都到叶子节点了，就不往下走了，而是继续下一个节点的判断
            }
            if(node.left!=null){
                nodeQue.addLast(node.left);
                valQue.addLast(node.left.val+value);
            }
            if(node.right!=null){
                nodeQue.addLast(node.right);
                valQue.addLast(node.right.val+value);
            }
        }
        return false;
    }
}

leetcode 113 号算法题：路径总和 II

//深度优先
class Solution {
    public List<List<Integer>> pathSum(TreeNode root,int targetSum) {
        List<List<Integer>> res=new ArrayList<>();
        if(root==null) return res;
        LinkedList<Integer> path=new LinkedList<>();
        dfs(root, targetSum,res, path);
        return res;
    }
    private void dfs(TreeNode node,int targetSum,List<List<Integer>> res, LinkedList<Integer> path){
        if(node==null) return;
        path.addLast(node.val);
        if(node.left==null&&node.right==null&&targetSum==node.val)
            res.add(new LinkedList<>(path));
        dfs(node.left,targetSum-node.val,res,path);
        dfs(node.right,targetSum-node.val,res,path);
        path.removeLast();
    }
}
或
//广度优先
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> list = new ArrayList<>();
        if (root == null) return list;
        List<Integer> path = new ArrayList<>();
        Stack<TreeNode> s = new Stack<>();
        int pathSum = 0;
        TreeNode lastVisited = null;
        TreeNode curr = root;
        while (curr != null || !s.isEmpty()){
              //把每个节点都当做根节点处理，并且把这个根节点的所有子节点都加入到栈中
            //所有节点入栈都从这里添加,一条路径所有节点的累加和都在这里进行
            while (curr != null){// 1. 遍历搜索左边的节点，一直到叶子节点
                s.push(curr);// 将节点压入栈中
                path.add(curr.val);// 将当前的节点加入当前的路径中
                pathSum += curr.val;// 累计计算当前 path 的总和
                curr = curr.left;
            }
            // 2. 访问左节点的右子树:先拿到左节点，这里使用 peek() 的原因：如果这个左节点有右子树的话，我们就不用再一次 push 到栈中
            curr = s.peek();
            if (curr.right != null && curr.right != lastVisited){// 条件：有右子树，并且右子树还没有访问过
                curr = curr.right;// 访问右子树
                continue; // 跳出外面的循环，来处理当前左节点的右子树
                //这里是为了把所有节点都当做根节点处理，即把当前节点放到while (curr!=null){这个循环中去处理
            }
            //能走到这里的路径一定是一条从根节点到叶子节点的路径,从这以下的代码都是对叶子节点的操作
            // 3. 检查是否符合路径和的条件：节点的左右子节点都为 null，并且路径总和等于目标值 sum
            if (curr.left == null && curr.right == null && pathSum == sum){// 当前路径符合条件，加入到返回结果中
                list.add(new ArrayList<Integer>(path));
            }
            s.pop();// 出栈当前的节点，因为已经处理完了
            lastVisited = curr; // 标记当前节点已经被访问，免得在这里被重复访问if (curr.right != null 
            pathSum -= curr.val; // 当前路径总和减去当前的节点值
            path.remove(path.size() - 1);// 当前路径中删除掉最后一个节点(也就是当前节点)
            curr = null; // 将当前的节点设置为 null，这是为了下次循环的时候从栈中拿到节点来进行处理，也是防止再次进去 while (curr != null){这个循环中
        }
        return list;
    }

leetcode 46 号算法题：全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
题解：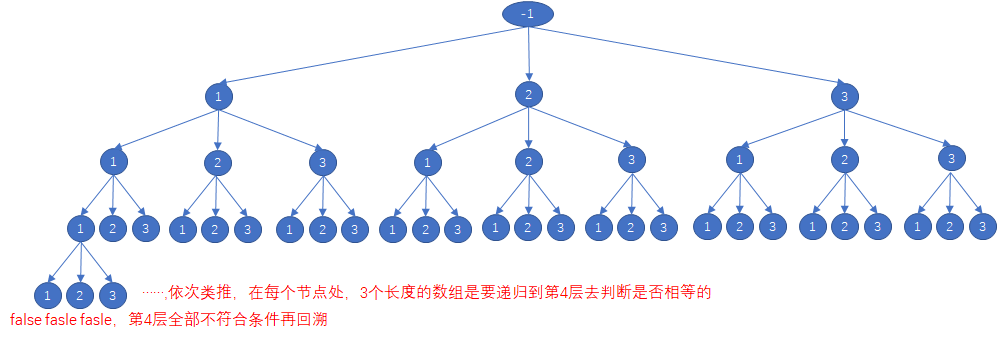

//过程1：可以选取重复数字的排列
public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    dfs(nums, -1, path, res);
    return res;
}
private void dfs(int[] nums, int index,List<Integer> path,List<List<Integer>> res) {
    if (path.size() == nums.length) {
        return;
    }
    if (index != -1) path.add(nums[index]);
    if (path.size() == nums.length) {
        res.add(new ArrayList<>(path));
    }
    for(int i=0;i<nums.length;i++){
        dfs(nums, i, path, res);
    }
    if (index != -1) path.remove(path.size() - 1); // 回溯的过程中，将当前的节点从 path 中删除
}
//过程2：合并回溯条件和添加排列（但是每种排列都被重复添加了多次）
public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    dfs(nums, -1, path, res);
    return res;
}
private void dfs(int[] nums, int index,List<Integer> path,List<List<Integer>> res) {
    if (path.size() == nums.length) {
        res.add(new ArrayList<>(path));
        return;
    }
    if (index != -1) path.add(nums[index]);
    for(int i=0;i<nums.length;i++){
        dfs(nums, i, path, res);
    }
    if (index != -1) path.remove(path.size() - 1);// 回溯的过程中，将当前的节点从 path 中删除
}
//过程3：去除过程2中的重复，回到过程1中的可以选取重复数字的排列，总结出回溯算法框架代码
public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    dfs(nums, -1, path, res);
    return res;
}
private void dfs(int[] nums, int index,List<Integer> path,List<List<Integer>> res) {
    if (path.size() == nums.length) {
        res.add(new ArrayList<>(path));
        return;
    }
    for(int i=0;i<nums.length;i++){
        path.add(nums[i]);//添加当前节点
        dfs(nums, i, path, res);
        path.remove(path.size() - 1); // 回溯的过程中，将当前的节点从 path 中删除
    }
}
过程4：找到全排列组合(利用contains方法来进行判断，其中，index也是不需要的方法参数，可以去掉)
public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    dfs(nums,  path, res);
    return res;
}
private void dfs(int[] nums,List<Integer> path,List<List<Integer>> res) {
    if (path.size() == nums.length) {
        res.add(new ArrayList<>(path));
        return;
    }
    for(int i=0;i<nums.length;i++){//这个循环时间复杂度为O(N^2),for循环O(n),contains()方法O(n)
        if(path.contains(nums[i])) continue;
        path.add(nums[i]);//添加当前节点
        dfs(nums, path, res);
        path.remove(path.size() - 1); // 回溯的过程中，将当前的节点从 path 中删除
    }
}
//过程5:从过程4的时间复杂度O(N!*N^2)优化到了O(N!*N)
public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    boolean[] used=new boolean[nums.length];
    dfs(nums,  path, res,used);
    return res;
}
private void dfs(int[] nums,List<Integer> path,List<List<Integer>> res,boolean[] used) {
    if (path.size() == nums.length) {
        res.add(new ArrayList<>(path));
        return;
    }
    for(int i=0;i<nums.length;i++){//这个循环时间复杂度为O(N),for循环O(n),判断为O(1)
        if(used[i]) continue;
        path.add(nums[i]);//添加当前节点
        used[i]=true;
        dfs(nums, path, res,used);
        path.remove(path.size() - 1); // 回溯的过程中，将当前的节点从 path 中删除
        used[i]=false;
    }
}

leetcode 47 号算法题：全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

//整体思路用一句话表示，两数相同时，前面的数据没插入，后面数据也不会插入
第二条由以下条件进行判断，两数相同时（nums[i] == nums[i - 1]），当前一个数没有递归时（!vis[i - 1]），则当前数据不递归（continue），这条规则保证了递归过程中，相同数据加入递归的顺序始终为坐标位置的顺序，即相同数据不排序（当然第二条的前提是数组必须排序，使相同的数据相邻）
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        boolean[] used=new boolean[nums.length];
        Arrays.sort(nums);
        dfs(res,path,nums,used);
        return res;
    }
    private void dfs(List<List<Integer>> res,List<Integer> path,int[] nums,boolean[] used){
        if(path.size()==nums.length){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0;i<nums.length;i++){
            //当前元素被用过了就跳过
            //走到后面这个判断条件一定是used[i]==false，即当前元素没有被用过，且
            if(used[i] || (i>0 && nums[i]==nums[i-1]&&!used[i-1]))
                continue;
            path.add(nums[i]);
            used[i]=true;
            dfs(res,path,nums,used);
            path.remove(path.size()-1);
            used[i]=false;
        }
    }
}
或
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        boolean[] used=new boolean[nums.length];
        Arrays.sort(nums);
        dfs(res,path,nums,used);
        return res;
    }
    private void dfs(List<List<Integer>> res,List<Integer> path,int[] nums,boolean[] used){
        if(path.size()==nums.length){
            res.add(new ArrayList<>(path));
            return;
        }
        int prev=Integer.MAX_VALUE;
        for(int i=0;i<nums.length;i++){
            if(used[i] || prev==nums[i])
                continue;
            path.add(nums[i]);
            used[i]=true;
            dfs(res,path,nums,used);
            path.remove(path.size()-1);
            used[i]=false;
            prev=nums[i];
        }
    }
}

leetcode 77 号算法题：组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        dfs(n,k,path,res);
        return res;
    }
    private void dfs(int n,int k, List<Integer> path,List<List<Integer>> res){
        if(path.size()==k){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=1;i<=n;i++){
            if(path.size()>0&&path.get(path.size()-1)>=i)
                continue;
            path.add(i);
            dfs(n, k, path, res);
            path.remove(path.size()-1);
        }
    }
}

leetcode 39 号算法题：组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明：
所有数字（包括 target）都是正整数。
解集不能包含重复的组合。
示例 1：
输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
[7],
[2,2,3]
]
题解：
在当前的函数中，每次我们可以选择跳过不用第 index 个数，即执行 dfs(target, path, index + 1)。
也可以选择使用第 index 个数，即执行 dfs(target - candidates[index ], path, index )，注意到每个数字可以被无限制重复选取，因此搜索的下标仍为 index。

class Solution {
     public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        dfs(candidates, target, res, path, 0);
        return res;
    }
    public void dfs(int[] candidates,int target,List<List<Integer>> res,List<Integer> path,int index) {
        if (index==candidates.length) {
            return;
        }
        if (target==0) {
            res.add(new ArrayList<>(path));
            return;
        }
        dfs(candidates,target,res,path,index+1);// 直接跳过
        if (target-candidates[index]>=0) {// 选择当前数
            path.add(candidates[index]);
            dfs(candidates,target-candidates[index],res,path,index);
            path.remove(path.size() - 1);
        }//此处是target <= 0时，就自然而然的结束了这个方法，所以不用加在递归条件里面
    }
}
或
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        dfs2(candidates,target,0,path,res,0);
        return res;
    }
    private void dfs2(int[] candidates, int target,int pathSum,List<Integer> path,List<List<Integer>> res,int index){
        if(index==candidates.length||pathSum>target)
            return;
        if(target==pathSum){
            res.add(new ArrayList<>(path));
            return;
        }
        dfs2(candidates, target, pathSum, path, res, index+1);
        if(pathSum<target){
            path.add(candidates[index]);
            dfs2(candidates, target, pathSum+candidates[index], path, res, index);
            path.remove(path.size()-1);
        }
    }
}

leetcode 40 号算法题：组合总和 Ⅱ

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明：
所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    List<List<Integer>> res=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    Arrays.sort(candidates);// 排序方便进行剪枝
    dfs(res,path,candidates,0,target);
    return res;
}
private void dfs(List<List<Integer>> res,Deque<Integer> path,int[] candidates,int index,int target){
    if (target==0){
        res.add(new ArrayList<>(path));
        return;
    }
    for (int i=index;i<candidates.length;i++){
        // 大剪枝：减去 candidates[i] 小于 0，减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0，因此用 break
        if (target-candidates[i]<0) break;
        // 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，因此跳过，用 continue
        if (i > index && candidates[i] == candidates[i - 1]) {
            continue;
        }
        path.addLast(candidates[i]);
        dfs(res,path,candidates,i+1,target-candidates[i]);
        path.removeLast();
    }
}
或
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> res=new ArrayList<>();
        LinkedList<Integer> path=new LinkedList<>();
        Arrays.sort(candidates);// 排序方便进行剪枝
        dfs(res,path,candidates,0,target);
        return res;
    }
    private void dfs(List<List<Integer>> res,Deque<Integer> path,int[] nums,int index,int target){
        if (index>nums.length) return;
        if (target==0){
            res.add(new ArrayList<>(path));
            return;
        }
        List<Integer> pre=new ArrayList<>(nums.length);
        for (int i=index;i<nums.length;i++){// 此处遍历决定的是每一个位置的数字的值
            if (pre.contains(nums[i])) continue;
            if (target-nums[i]<0) break; // 剪枝
            pre.add(nums[i]);
            path.addLast(nums[i]);
            dfs(res,path,nums,i+1,target-nums[i]);
            path.removeLast();
        }
    }
}

leetcode 216 号算法题：组合总和 Ⅲ

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。
说明：
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

class Solution {
    public List<List<Integer>> combinationSum3(int k, int n) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        dfs(n,k,path,res);
        return res;
    }
    private void dfs(int n, int k, List<Integer> path, List<List<Integer>> res) {
        if(path.size()>k||n<0){
            return;
        }
        if(path.size()==k&&n==0){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=1;i<=9;i++){
            if(path.size()>0&&path.get(path.size()-1)>=i)
                continue;
            path.add(i);
            dfs(n-i, k, path, res);
            path.remove(path.size()-1);
        }
    }
}

leetcode 78 号算法题：子集

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。
解集 不能包含重复的子集。你可以按任意顺序返回解集。
示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        Arrays.sort(nums);
        dfs(nums,0,path,res);
        return res;
    }
    private void dfs(int[] nums, int index, List<Integer> path, List<List<Integer>> res) {
        if(index==nums.length){
            res.add(new ArrayList<>(path));
            return;
        }
        dfs(nums, index+1, path, res);
        path.add(nums[index]);
        dfs(nums, index+1, path, res);
        path.remove(path.size()-1);
    }
}
或
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        Arrays.sort(nums);
        dfs(nums,0,path,res);
        return res;
    }
    private void dfs(int[] nums, int index,List<Integer> path, List<List<Integer>> res) {
        if(path.size()<=nums.length){
            res.add(new ArrayList<>(path));
        }
        for(int i=0;i<nums.length;i++){
            if(path.size()>0&&path.get(path.size()-1)>=nums[i]) continue;
            path.add(nums[i]);
            dfs(nums, index+1,path, res);
            path.remove(path.size()-1);
        }
    }
}
或
class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        for (int mask = 0; mask < (1 << n); ++mask) {
            path.clear();
            for (int i = 0; i < n; ++i) {//这里n是固定的
                if ((mask & (1 << i)) != 0) {
                    path.add(nums[i]);
                }
            }
            res.add(new ArrayList<>(path));
        }
        return res;
    }
}

leetcode 90 号算法题：子集Ⅱ

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。
解集 不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。
示例 1：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        Arrays.sort(nums);
        dfs(nums,0,path,res);
        return res;
    }
    private void dfs(int[] nums, int index,List<Integer> path, List<List<Integer>> res) {
        if(path.size()<=nums.length){
            res.add(new ArrayList<>(path));
        }
        List<Integer> pre=new ArrayList<>();
        for(int i=index;i<nums.length;i++){
            if((path.size()>0&&path.get(path.size()-1)>nums[i])||pre.contains(nums[i])) continue;
            pre.add(nums[i]);
            path.add(nums[i]);
            dfs(nums, i+1, path, res);
            path.remove(path.size()-1);
        }
    }
}

leetcode 17 号算法题：电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
示例 1：
输入：digits = “23”
输出：[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]

class Solution {
    public List<String> letterCombinations(String digits) {
        List<String> res=new ArrayList<>();
        if(digits==null||digits.length()==0)
            return res;
        HashMap<Character,String> map=new HashMap<>();
        map.put('2', "abc");
        map.put('3', "def");
        map.put('4', "ghi");
        map.put('5', "jkl");
        map.put('6', "mno");
        map.put('7', "pqrs");
        map.put('8', "tuv");
        map.put('9', "wxyz");
        dfs(digits,0,map,new StringBuilder(),res);
        return res;
    }
    private void dfs(String digits,int index,HashMap<Character,String> map,StringBuilder builder,List<String> res) {
        if(builder.length()==digits.length()){
            res.add(builder.toString());
        }else {
            char ch = digits.charAt(index);
            String str = map.get(ch);
            int len=str.length();
            for(int i=0; i<len;i++){
                builder.append(str.charAt(i));
                dfs(digits, index+1, map, builder, res);
                builder.deleteCharAt(builder.length()-1);
            }
        }
    }
}
或
class Solution {
    public List<String> letterCombinations(String digits) {
        List<String> res=new ArrayList<>();
        if(digits==null||digits.length()==0)
            return res;
        HashMap<Character,String> map=new HashMap<>();
        map.put('2', "abc");
        map.put('3', "def");
        map.put('4', "ghi");
        map.put('5', "jkl");
        map.put('6', "mno");
        map.put('7', "pqrs");
        map.put('8', "tuv");
        map.put('9', "wxyz");
        dfs(digits,0,map,"",res);
        return res;
    }
    private void dfs(String digits, int index, HashMap<Character,String> map, String str, List<String> res) {
        if(str.length()==digits.length()){
            res.add(str);
        }else {
            char ch = digits.charAt(index);
            String temp = map.get(ch);
            for(char strToCh:temp.toCharArray()){
                dfs(digits, index+1, map, str+strToCh, res);
            }
        }
    }
}

leetcode 93 号算法题：复原 IP 地址

给定一个只包含数字的字符串，用以表示一个 IP 地址，返回所有可能从 s 获得的有效 IP 地址。你可以按任何顺序返回答案。有效 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。
例如：”0.1.2.201” 和 “192.168.1.1” 是有效 IP 地址，但是 “0.011.255.245”、”192.168.1.312” 和 “192.168@1.1” 是无效 IP 地址。
示例 1：
输入：s = “25525511135”
输出：[“255.255.11.135”,”255.255.111.35”]

class Solution {
    public List<String> restoreIpAddresses(String s) {
        List<String> res = new ArrayList<>();
        int len=s.length();//要分割的字符串长度
        if (len<4||len>12) { //如果长度不够或者过大，则不搜索
            return res;
        }
        Deque<String> path=new ArrayDeque<>(4);//存放每一个符合规则的ip地址
        int splitTimes=0;//已经分割成ip地址的段数
        dfs(s,len,splitTimes,0,path,res);
        return res;
    }
    //判断 s 的子区间 [left, right] 是否能够成为一个 ip 段。判断的同时顺便把类型转了
    private int judgeIfIpSegment(String s,int left,int right){
        int len=right-left + 1;
        if(len>1&&s.charAt(left)=='0') {//大于1位的时候，不能以0开头
            return -1;
        }
        int res=0;
        for (int i=left;i<=right;i++) { //转成int类型
            res=res*10+s.charAt(i)-'0';
        }
        if (res>255) {//大于255不是合法的 ip 段数值
            return -1;
        }
        return res;
    }
    private void dfs(String s,int len,int split,int begin,Deque<String> path,List<String> res) {
        if (begin==len) {//到达字符串末尾
            if (split==4) {//并且分隔成为了4段的ip
                res.add(String.join(".", path));
            }
            return;
        }
        // 看到剩下位数的不够或者超出了，就退出（剪枝），len-begin表示剩余的还未分割的字符串的位数
        if (len-begin<(4-split)||len-begin >3*(4-split)) {
            return;
        }
        for (int i=0;i<3;i++) {//每个ip地址段都可以取1-3位的数字
            if (begin+i>=len) {//剩下的数字不够取了，则结束
                break;
            }
            int ipSegment=judgeIfIpSegment(s,begin,begin + i);
            if (ipSegment!=-1) { // 在判断是 ip 段的情况下，才去做截取
                path.addLast(ipSegment + "");
                dfs(s,len,split + 1,begin+i+1,path,res);
                path.removeLast();
            }
        }
    }
}
或
public class Solution {
    static final int SEG_COUNT=4;
    List<String> res=new ArrayList<>();
    int[] segments=new int[SEG_COUNT];
    public List<String> restoreIpAddresses(String s) {
        dfs(s,0,0);
        return res;
    }
    public void dfs(String s,int segId,int segStart) {
        if (segId==SEG_COUNT) {// 如果找到了 4 段 IP 地址
            if (segStart==s.length()) {//并且遍历完了字符串，那么就是一种答案
                StringBuffer ipAddr=new StringBuffer();
                for (int i=0;i<SEG_COUNT;i++) {
                    ipAddr.append(segments[i]);
                    if (i!=SEG_COUNT-1) {//不是最后一段的话，就加上ip地址的分割符号 .
                        ipAddr.append('.');
                    }
                }
                res.add(ipAddr.toString());
            }
            return;
        }
        if (segStart==s.length()) { //能走到这，说明还没有找到4段IP地址，但已经遍历完了字符串，那么提前回溯
            return;
        }
        if (s.charAt(segStart)=='0') {//由于不能有前导零，如果当前数字为 0，那么这一段 IP 地址只能为 0
            segments[segId] = 0;
            dfs(s,segId+1,segStart+1);
        }
        int addr=0; //一般情况，枚举每一种可能性并递归
        for (int segEnd=segStart;segEnd<s.length();segEnd++) {
            addr =addr*10+(s.charAt(segEnd)-'0');
            if(addr>0&&addr<=0xFF){
                segments[segId]=addr;
                dfs(s,segId+1,segEnd + 1);
            }else{
                break;
            }
        }
    }
}

leetcode 22 号算法题：括号生成

https://leetcode-cn.com/problems/generate-parentheses/solution/pei-yang-chou-xiang-si-wei-hui-su-jie-fa-7dwu/
数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。
示例 1：
输入：n = 3
输出：[“((()))”,”(()())”,”(())()”,”()(())”,”()()()”]
示例 2：
输入：n = 1
输出：[“()”]
提示：
1 <= n <= 8

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> res=new ArrayList<>();
        if(n<1) return res;
        dfs(n,"",res,0,0);
        return res;
    }
    private void dfs(int n,String path,List<String> res,int open,int close){
        if(close>open||open>n)
            return;
        if(2*n==path.length()){
            res.add(path);
            return;
        }
        dfs(n, path+"(", res,open+1,close);
        dfs(n, path+")", res,open,close+1);
    }
}
或
class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> res=new ArrayList<>();
        if(n<1) return res;
        dfs(n,"",res,0,0);
        return res;
    }
    private void dfs(int n,String path,List<String> res,int open,int close){
        if(2*n==path.length()){
            res.add(path);
            return;
        }
        if(open<n)
            dfs(n, path+"(", res,open+1,close);
        if(close<open)
            dfs(n, path+")", res,open,close+1);
    }
}

leetcode 51 号算法题：N 皇后

//找到所有的n皇后摆放位置
class Solution {
    private void check(int[] array,int max,int n,List<int[]> res){//放置第n个皇后
        if(n==max){
            res.add(Arrays.copyOf(array, array.length));
            return;
        }
        for(int i=0;i<max;i++){//放置第n个皇后时：从这行0-max处一次放置，看是否会冲突
            array[n]=i;
            if(judge(array,n)){//当前位置不冲突，则放置下一个皇后
                check(array,max,n+1,res);
            }
        }
    }
    private boolean judge(int[] array,int n){//判断当前皇后放在此处(这行的第n个位置)是否冲突
        for(int i=0; i<n;i++){//与前n-1个皇后的位置进行比较，看是否冲突
            //array[i] == array[n] 看是否在同一列上
            //Math.abs(n - i) == Math.abs(array[n] - array[i]) 看是否在同一斜线上
            if (array[i]==array[n]||Math.abs(n-i)==Math.abs(array[n]-array[i])){
                return false;
            }
        }
        return true;
    }
}

class Solution {
    public List<List<String>> solveNQueens(int n) {
        int[] array=new int[n];
        List<List<String>> res=new ArrayList<>();
        check(array, n, 0, res);
        return res;
    }
    private void check(int[] array,int max,int n,List<List<String>> res){//放置第n个皇后
        if(n==max){
            List<String> path=new ArrayList<>();
            for(int i=0;i<max;i++){
                char[] chars=new char[max];
                Arrays.fill(chars, '.');
                chars[array[i]]='Q';
                path.add(new String(chars));
            }
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0;i<max;i++){//放置第n个皇后时：从这行0-max处一次放置，看是否会冲突
            array[n]=i;
            if(judge(array,n)){//当前位置不冲突，则放置下一个皇后
                check(array,max,n+1,res);
            }
        }
    }
    private boolean judge(int[] array,int n){//判断当前皇后放在此处(这行的第n个位置)是否冲突
        for(int i=0; i<n;i++){//与前n-1个皇后的位置进行比较，看是否冲突
            //array[i] == array[n] 看是否在同一列上
            //Math.abs(n - i) == Math.abs(array[n] - array[i]) 看是否在同一斜线上
            if (array[i]==array[n]||Math.abs(n-i)==Math.abs(array[n]-array[i])){
                return false;
            }
        }
        return true;
    }
}
或
class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> res=new ArrayList<>();
        char[][] board=new char[n][n];
        for (int i=0;i<board.length;i++) {
            Arrays.fill(board[i],'.');
        }
        check(board, 0, res);
        return res;
    }
    private void check( char[][] board,int index,List<List<String>> res){
        if(index==board.length){
            List<String> temp=new ArrayList<>();
            for (int i=0;i<board.length;i++) {
                temp.add(new String(Arrays.copyOf(board[i],board.length)));
            }
            res.add(new ArrayList<>(temp));
            return;
        }
        for(int i=0;i<board.length;i++){//列
            if(isVisited(board,index,i,'Q'))
                continue;
            board[index][i]='Q';
            check(board, index+1, res);
            board[index][i]='.';
        }
    }
    private boolean isVisited(char[][] board, int row, int col, char target) {
        for (int i=0; i<row; i++) {
            if(board[i][col]==target)
                return true;
        }
        if(row>0&&col>0) {
            for (int i=row-1,j=col-1;i>=0&&j>=0;i--,j--) { //左上角
                if (board[i][j] == target)
                    return true;
            }
        }
        if(row>0){
            for(int i=row-1,j=col+1;i>=0&&j<board.length;i--,j++){ //右上角
                if(board[i][j]==target)
                    return true;
            }
        }
        return false;
    }
}

leetcode 37 号算法题：数独问题

class Solution {
    public void solveSudoku(char[][] board) {
        backtrack(board, 0, 0);
    }
    private boolean backtrack(char[][] board,int i,int j){//i是行，j是列
        if(j==board[0].length){
           return backtrack(board, i+1, 0);
        }
        if(i==board.length){
            return true;
        }
        if(board[i][j]!='.'){
            return backtrack(board, i, j+1);
        }
        for(char ch='1';ch<='9';ch++){
            if(isVisited(board,i,j,ch)) {
                continue;
            }
            board[i][j]=ch;
            if(backtrack(board, i, j+1))
                return true;
            board[i][j]='.';
        }
        return false;
    }
    private boolean isVisited(char[][] board,int m,int n,char target) {
        for(int i=0;i<board.length;i++){
            if(board[m][i]==target)
                return true;
            if(board[i][n]==target)
                return true;
            if(board[(m/3)*3+i/3][(n/3)*3+i%3]==target)
                return true;
        }
        return false;
    }
}

贪心算法思想

leetcode 455 号算法题：分发饼干

leetcode 322 号算法题：零钱兑换

leetcode 45 号算法题：跳跃游戏 Ⅱ

leetcode 1578 号算法题：避免重复字母的最小删除成本

leetcode 402 号算法题：移掉K位数字

动态规划算法思想

leetcode 509 号算法题：斐波那契数

leetcode 322 号算法题：零钱兑换

leetcode 64 号算法题：最小路径和

leetcode 53 号算法题：最大子数组之和

leetcode 647 号算法题：回文子串

leetcode 5 号算法题：最长回文串

leetcode 131 号算法题：分割回文串

leetcode 516 号算法题：最长回文子序列

leetcode 300 号算法题：最长上升子序列

leetcode 1143 号算法题：最长公共子序列

leetcode 72 号算法题：编辑距离

leetcode 44 号算法题：通配符匹配

leetcode 10 号算法题：正则表达式匹配

leetcode 486 号算法题：预测赢家

leetcode 877 号算法题：石子游戏

0-1 背包问题

总结

1.深度优先搜索遍历二叉树的所有路径

//深度优先遍历
public List<List<Integer>> pathSum(TreeNode root) {
    List<List<Integer>> res=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    dfs(root,path,res);
    return res;
}
private void dfs(TreeNode node,LinkedList<Integer> path,List<List<Integer>> res){
    if(node==null) return;
    path.addLast(node.val);
    if(node.left==null&&node.right==null){
        res.add(new ArrayList<>(path));
    }
    dfs(node.left, path, res);
    dfs(node.right, path, res);
    path.removeLast();
}
或
List<List<Integer>> res=new ArrayList<>();
LinkedList<Integer> path=new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root) {
    dfs(root);
    return res;
}
private void dfs(TreeNode node){
    if(node==null) return;
    path.addLast(node.val);
    if(node.left==null&&node.right==null){
        res.add(new ArrayList<>(path));
    }
    dfs(node.left);
    dfs(node.right);
    path.removeLast();
}
//广度优先遍历
public List<List<Integer>> pathSum(TreeNode root) {
    List<List<Integer>> res=new ArrayList<>();
    Stack<TreeNode> stack=new Stack<>();
    List<Integer> path=new ArrayList<>();
    TreeNode curr=root;
    TreeNode lastVisited=null;
    while (curr!=null||!stack.isEmpty()){
        while (curr!=null){
            stack.add(curr);
            path.add(curr.val);
            curr=curr.left;
        }
        curr=stack.peek();
        if(curr.right!=null&&curr.right!=lastVisited){
            curr=curr.right;
            continue;
        }
        if(curr.right==null&&curr.left==null){
            res.add(new ArrayList<>(path));
        }
        path.remove(path.size()-1);
        curr=stack.pop();
        lastVisited=curr;
        curr=null;
    }
    return res;
}

四、刷题总结

1.关于递归反转链表

private ListNode traverse(ListNode head) {//反转整个链表
    if(head.next==null)
        return head;
    ListNode last=traverse(head.next);
    head.next.next=head;
    head.next=null;
    return last;
}
ListNode after;
private ListNode traverse(ListNode head,int m) {//反转链表的前n个节点
    if(m==1){
        after=head.next;
        return head;
    }
    ListNode last=traverse(head.next,m-1);
    head.next.next=head;
    head.next=after;
    return last;
}
private ListNode traverse(ListNode head,int m,int n) {//反转链表 m-n 之间的节点
    if(m==1){
        return traverse(head,n);
    }
    head.next=traverse(head.next,m-1,n-1);
    return head;
}

我的算法学习记录

一、排序算法

1.快速排序

基本思想：

快排示例：

2.归并排序

基本思想：

归并示例：

二、查找算法

1.二分查找

1.1经典二分问题

基本思想：

算法代码描述：

经典二分问题：

java代码实现:

1.2 基础二分小变形1

代码实现

1.3基础二分小变形2

查找某个目标值的边界

代码实现

1.4泛化二分的概念

与有序无序无关

代码实现

1.5在线性结构上二分的题目积累

例1：找峰值元素

例2：找原有序旋转数组的旋转后最小元素

例3：找原有序旋转数组是否存在某个目标值，并返回其索引

1.6二维数组的二分查找

判断 m x n 矩阵中，是否存在一个目标值

1.7二叉树上二分的题目积累

例1：先看一道简单的在二叉树上查找值。

例2：给出一个完全二叉树，求出该树的节点个数。

1..8数学中的二分

1.9最大化或最小化问题

三、回溯、贪心和动态规划

回溯算法思想

leetcode 112 号算法题：路径总和

leetcode 113 号算法题：路径总和 II

leetcode 46 号算法题：全排列

leetcode 47 号算法题：全排列 II

leetcode 77 号算法题：组合

leetcode 39 号算法题：组合总和

leetcode 40 号算法题：组合总和 Ⅱ

leetcode 216 号算法题：组合总和 Ⅲ

leetcode 78 号算法题：子集

leetcode 90 号算法题：子集Ⅱ

leetcode 17 号算法题：电话号码的字母组合

leetcode 93 号算法题：复原 IP 地址

leetcode 22 号算法题：括号生成

leetcode 51 号算法题：N 皇后

leetcode 37 号算法题：数独问题

贪心算法思想

leetcode 455 号算法题：分发饼干

leetcode 322 号算法题：零钱兑换

leetcode 45 号算法题：跳跃游戏 Ⅱ

leetcode 1578 号算法题：避免重复字母的最小删除成本

leetcode 402 号算法题：移掉K位数字

动态规划算法思想

leetcode 509 号算法题：斐波那契数

leetcode 322 号算法题：零钱兑换

leetcode 64 号算法题：最小路径和

leetcode 53 号算法题：最大子数组之和

leetcode 647 号算法题：回文子串

leetcode 5 号算法题：最长回文串

leetcode 131 号算法题：分割回文串

leetcode 516 号算法题：最长回文子序列

leetcode 300 号算法题：最长上升子序列

leetcode 1143 号算法题：最长公共子序列

leetcode 72 号算法题：编辑距离

leetcode 44 号算法题：通配符匹配

leetcode 10 号算法题：正则表达式匹配

leetcode 486 号算法题：预测赢家

leetcode 877 号算法题：石子游戏

0-1 背包问题

总结

1.深度优先搜索遍历二叉树的所有路径

四、刷题总结

1.关于递归反转链表