创造变量

基本符号运算

  1. x=sym(‘x’) 创建一个符号变量
  2. syms x y z 创建多个符号变量 x y z
  3. r=collec(S,v) 合并同类项，S是符号表达式，v是变量或表达式

合并同幂项

EXPR=sym(‘(x^2+xexp(-t)+1)(x+exp(-t))’); expr1=collect(EXPR) expr2=collect(EXPR,’exp(-t)’)

注解：

  1. 这里会报出警告，但不影响程序的运行

  2. exp(-t)的意思就是e的-t次方

    因式分解

    factor(S) 符号计算的因式分解，S是待分解的符号多项式

  3. 除了x外不含其他自由变量的情况

    sym a x; f1=x^4-5x^3+5x^2+5*x-6; factor(f1)

  4. 含其他自由变量的情况之一

    f2-x^2-a^2; factor(f2)

  5. 对正整数的质数分解

    factor(1025)

展开

expand(S) 对符号多项式或函数S进行展开

例如：

syms x y; expand((x+1)^3) expand(sin(x+y))

对符号表达式进行化简

r=simple(S) 或 r=simplify(S) 对符号表达式S进行化简

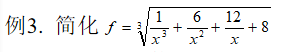
image.png

  1. 运用simplify简化

    syms x; f=(1/x^3+6/x^2+12/x+8)^(1/3); sfy1=simplify(f), sfy1=simplify(sfy1)

  2. 运用simple简化

    g1=simple(f), g2=simple(g1)

极限的运算

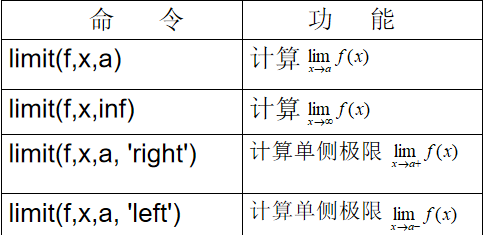
image.png

注意：在左右极限不相等或左右极限有一个不存在时，MATLAB的默认状态是求右极限。

例题1

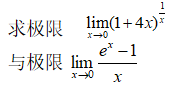
image.png

syms x;
y1=(1+4*x)^(1/x);
y2=(exp(x)-1) /x;
limit(y1,x,0)
limit(y2,x,0)

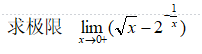
image.png

syms x;
y=sqrt(x)-2^(-1/x);
limit(y,x,0, ‘right’)

求导

一元函数的求导 diff(f)
对n求导 diff(f,n)

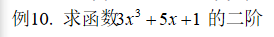
image.png

syms x;
f=3x^3+5x+1;
diff(f,2)

image.png

syms x;
y=3x^3-2x+1;
B=diff(y),x=1;
eval(B)

ps:eval函数的功能是将字符串转换为matlab可执行语句。通俗而言，比如 你输入 a=’b=1’; 会在workspace里看见生成了变量a，a的类型是字符串，字符串的内容是b=1 然后你输入eval(a) 就会看见变量里生成了变量b，b是一个1乘1的double型矩阵，元素的值为1 也就是说，执行eval(a)相当于执行a的内容，相当于执行b=1

多元函数的偏导数

diff(f,xi) diff(f,xi,n)

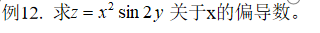
image.png

syms x y;
z=x^2sin(2y);
B=diff(z,x)

积分运算