本文是对 Swift Algorithm Club - Big-O notation 翻译的一篇文章。

Swift Algorithm Club是 raywenderlich.com网站出品的用Swift实现算法和数据结构的开源项目，目前在GitHub上有23.4K⭐️，大概有一百左右个的算法和数据结构，基本上常见的都包含了，是iOSer学习算法和数据结构不错的资源。

大O表示法简介

image.png
知道某个算法的运行速度和占用的内存空间，对于选择正确的算法来解决问题非常有帮助。

大O表示法 能让你对一个算法的运行时间和占用内存有个大概概念。当有人说，“这个算法在最糟情况下的运行时间是 O(n^2)，而且占用了 O(n) 大小的空间”时，他的意思是这个算法有点慢，不过没占多大内存。

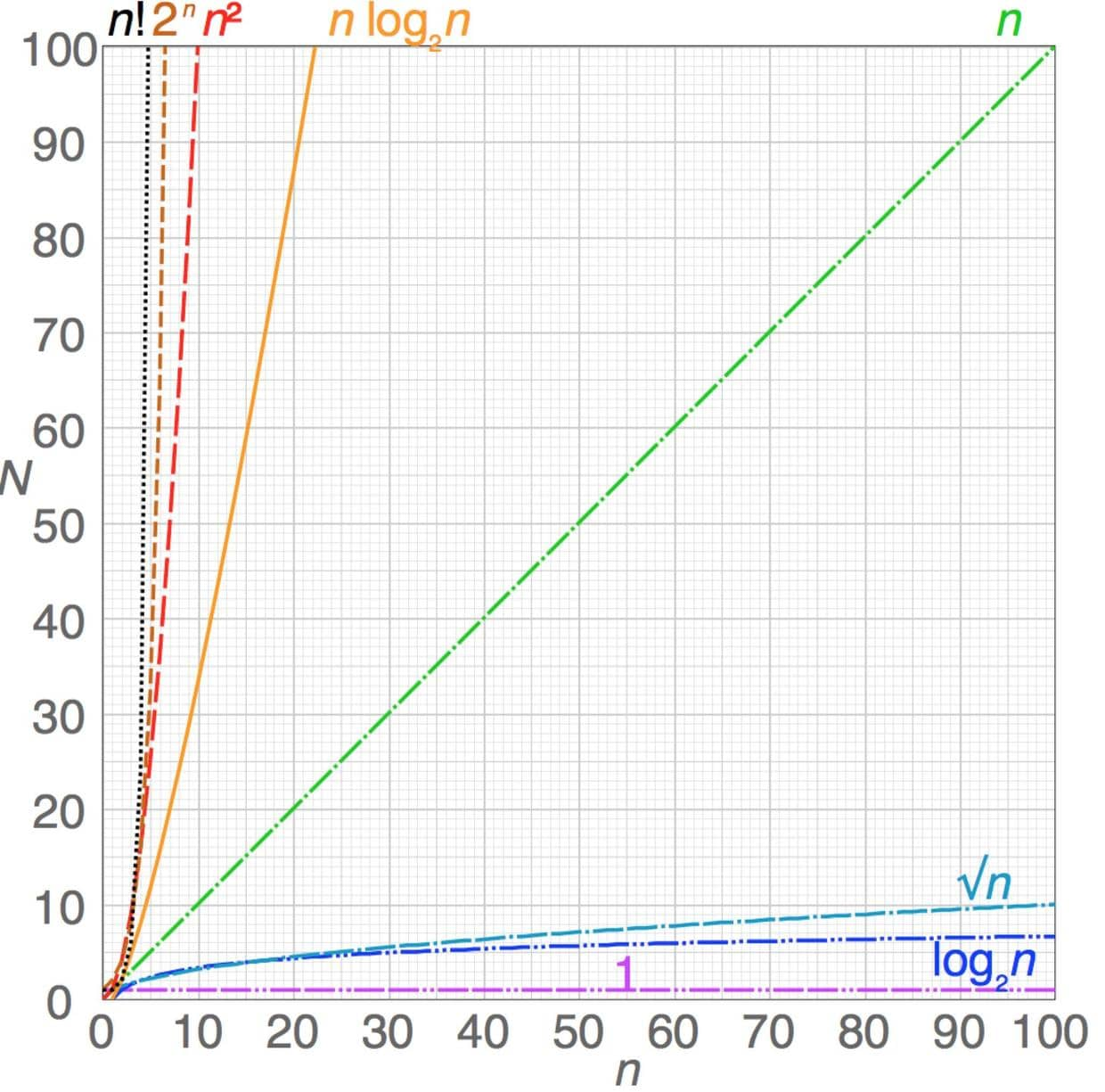
要知道一个算法的大O 表示法通常要通过数学分析。在这里我们不会涉及具体的数学，不过知道不同的值意味着什么会很有用。所以这里有一张方便的表。n 在这里代表的意思是数据的个数。举个例子，当对一个有 100 个元素的数组进行排序时，n = 100。

Big-O表示符号 名字 描述
O(1) 常数级 最好的。不论输入数据量有多大，这个算法的运行时间总是一样的。例子: 基于索引取出数组中对应的元素。
O(log n) 对数级 相当好。这种算法每次循环时会把需要处理的数据量减半。如果你有 100 个元素，则只需要七步就可以找到答案。1000 个元素只要十步。100,0000 元素只要二十步。即便数据量很大这种算法也非常快。例子：二分查找。
O(n) 线性级 还不错。如果你有 100 个元素，这种算法就要做 100 次工作。数据量翻倍那么运行时间也翻倍。例子：线性查找。
O(n log n) 线性对数级 还可以。比线性级差了一些，不过也没那么差劲。例子：最快的通用排序算法。
O(n^2) 二次方级 有点慢。如果你有 100 个元素，这种算法需要做 100^2 = 10000 次工作。数据量 x 2 会导致运行时间 x 4 (因为 2 的 2 次方等于 4)。例子：循环套循环的算法，比如插入排序。
O(n^3) 三次方级 特别慢。如果你有 100 个元素，那么这种算法就要做 100^3 = 100,0000 次工作。数据量 x 2 会导致运行时间 x 8。例子：矩阵乘法。
O(2^n) 指数级 超级慢。这种算法你要想方设法避免，但有时候你就是没得选。加一点点数据就会把运行时间成倍的加长。例子：旅行商问题。
O(n!) 阶乘级 比蜗牛还慢！不管干什么都要跑个 N 年才能得到结果。

以下是每种大O表示法的示例：

O(1)

O(1)复杂性的最常见示例是访问数组索引。

  1. let value = array[5]

另外一个O(1)的例子是栈的推进和弹出。

O(log n)

  1. var j = 1
  2.   while j < n {
  3.     // do constant time stuff
  4.     j *= 2
  5.   }

在每次运行中，“ j”不仅会简单地增加，而且会自身增加2倍，需要处理的数据量减半。
二进制搜索算法是O（log n）复杂度的一个示例。

O(n)

  1.   for i in stride(from: 0, to: n, by: 1) {
  2.     print(array[i])
  3.   }

数组遍历和线性搜索是O(n)复杂性的示例。

O(n log n)

  1. for i in stride(from: 0, to: n, by: 1) {
  2. var j = 1
  3.   while j < n {
  4.     j *= 2
  5.     // do constant time stuff
  6.   }
  7. }

或

  1. for i in stride(from: 0, to: n, by: 1) {
  2.   func index(after i: Int) -> Int? { // multiplies `i` by 2 until `i` >= `n`
  3.     return i < n ? i * 2 : nil
  4.   }
  5.   for j in sequence(first: 1, next: index(after:)) {
  6.     // do constant time stuff
  7.   }
  8. }

合并排序和堆排序是O(n log n)复杂度的示例。

O(n^2)

  1. for i  in stride(from: 0, to: n, by: 1) {
  2.   for j in stride(from: 1, to: n, by: 1) {
  3.     // do constant time stuff
  4.   }
  5. }

遍历简单的二维数组和冒泡排序是O(n^2)复杂度的示例。

O(n^3)

  1. for i in stride(from: 0, to: n, by: 1) {
  2.   for j in stride(from: 1, to: n, by: 1) {
  3.     for k in stride(from: 1, to: n, by: 1) {
  4.       // do constant time stuff
  5.     }
  6.   }
  7. }

O(2^n)

  1. func solveHanoi(n: Int, from: String, to: String, spare: String) {
  2.   guard n >= 1 else { return }
  3.   if n > 1 {
  4.       solveHanoi(n: n - 1, from: from, to: spare, spare: to)
  5.       solveHanoi(n: n - 1, from: spare, to: to, spare: from)
  6.   }
  7. }

运行时间为O（2 ^ N）的算法通常是递归算法，通过递归求解大小为N-1的两个较小问题来解决大小为N的问题。 以下示例显示解决了著名的N盘“汉诺塔”问题所需的所有动作。

O(n!)

下面给出了O(n!)的最简单的例子。

  1. func nFactFunc(n: Int) {
  2.   for i in stride(from: 0, to: n, by: 1) {
  3.     nFactFunc(n: n - 1)
  4.   }
  5. }

大部分情况下你用直觉就可以知道一个算法的大O 表示法，不需要使用数学。比如说，如果你的代码用一个循环遍历你输入的每个元素，那么这个算法就是 O(n)。如果是循环嵌套循环，那就是 O(n^2)。如果3个循环嵌套在一起就是 O(n^3)，以此类推。

注意，大O 表示法只是一种估算，当数据量大的时候才有用。举个例子，插入排序的最糟情况运行时间是 O(n^2)。 理论上来说它的运行时间比归并排序要慢一些，归并排序是 O(n log n)。但对于小数据量，插入排序实际上更快一些，特别是那些已经有一部分数据是排序好的数组。

如果你看完没懂，也不要太纠结了。这种东西仅仅在比较两种算法哪种更好的时候才有点用。但归根结底，你还是要实际测试之后才能得出结论。而且如果数据量相对较小，哪怕算法比较慢，在实际使用也不会造成太大的问题。