二分法

二分法用于在有序数列中查值或查范围。时间复杂度O(logn)
对于查值，正统的模板如下。low与high的更新都是mid+1或mid-1，循环条件为low<=high。这种写法二分的效率最高。

class Solution {
    public int search(int[] nums, int target) {
        int low = 0, high = nums.length - 1;
        while (low <= high) {
            int mid = (high - low) / 2 + low;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return -1;
    }
}

对于一般的查找，可以使用以下模板：
思路一：
以获得第一个>=target的数的下标为例，可画出如下图。红字“二分位置”是满足条件的位置。使用一个额外的变量 pos 记录满足条件的位置。在判断条件时，结合下图决定给 pos 赋值应该放在哪个条件块中。

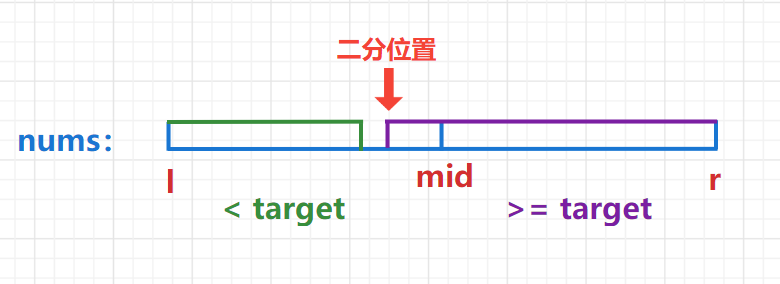
// 以获得第一个>=target的数的下标为例
public int my_binary_search(int nums[], int target){
    int low = 0, high = nums.length - 1, pos=-1;
    while (low <= high) { // 此种循环最终必然会导致 left > high
        int mid = (high - low) / 2 + low;
        if(nums[mid] < target){
            low=mid+1;
        }else{
            pos=mid;  // else条件块代表紫色区域，是有可能作为结果的，在此处更新pos的值
            high=mid-1;
        }
    }
    return pos;
}

思路二：
以获得第一个>=target的数的下标为例，可画出如下图。红字“二分位置”是满足条件的位置。二分就是通过缩小[low, high]的范围锁定这个位置，因此每次更新的 low与high都应该是【可能满足条件的位置】。
如果nums[mid] < target，说明mid位置不可能满足条件了，因此 low=mid+1;
如果nums[mid] >= target，说明mid位置【有可能满足条件】，因此 high=mid;
最后一定会将[low, high]缩小至low==high，返回high。由于high有可能一直没有更新（比如全部数都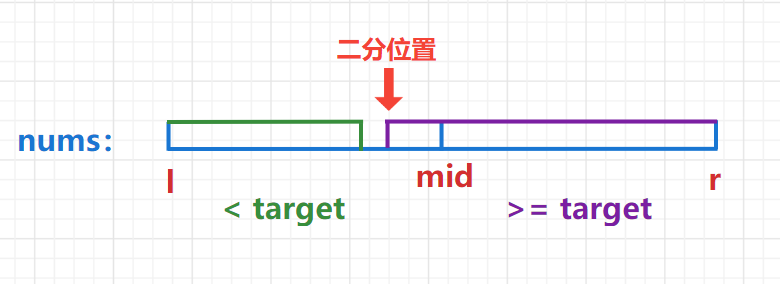

// 以获得第一个>=target的数的下标为例
public int my_binary_search(int nums[], int target){
    int low = 0, high = nums.length - 1;
    while (low != high) { //此种循环最终必然会将问题规模缩减至1
        int mid = (high - low) / 2 + low;
        int noUse = nums[mid] < target ? (low=mid+1) : (high=mid);
    }
    if(high==nums.length-1 && nums[high]<target){
        return -1; // 没有>=target的数
    }
    return high;
}