连续数的和

  1. #include <iostream>
  2. using namespace std;
  4. int CountSum(int n);
  6. int main() {
  7.     int nId = 0;
  8.     int nSum;                   //int为32位
  9.     int nOut[1000] = { 0 };     //题目要求，1≤T≤1000 ，T=nId
  10.     int *pInt = nOut;
  11.     cin >> nId;
  12.     for (int i = 0; i < nId; i++)
  13.     {
  14.         cin >>  nSum;
  15.         pInt[i] = CountSum(nSum);
  16.     }
  17.     for (int i = 0; i < nId; i++)
  18.         cout << "Case #" << (i + 1) << ": " << pInt[i] << endl;
  19.     system("pause");
  20.     return 0;
  21. }
  22. int CountSum(int sum) {
  23.     int nSum = 0;
  24.     int temp = 0;
  25.     //sum = k * (2 * i + k - 1) / 2; 等差数列求和公式
  26.     for (int k = 2; k <= (sum+1)/2; k++) {       //题目要求至少包括两个整数,(sum+1)/2确保始终取到中间值
  27.         if (2 * sum % k == 0) {
  28.             temp = 2 * sum / k - k + 1;
  30.             if (temp>0&&temp % 2 == 0) {  //按照正项等差数列，首项、公比、数列和必须为正整数
  31.                 ++nSum;
  32.             }
  33.         }
  34.     }
  35.     return nSum;
  36. }
#include<iostream>
#include<math.h>
using namespace std;
int function(int n)
{
    int count = 0;       // count用来保存最后的结果
    double a1;
    int N = (int)(0.5*(-1 + sqrt(1 + 8 * n)));
    for (int cnt = 2; cnt <= N; ++cnt) {            从2开始枚举 
        a1 = 1.0*n / cnt - cnt / 2.0 + 1 / 2.0;
        if ((int)a1 == a1 && a1 > 0) {     //  如果得到的a1为整数且a1大于0 ，那么就符合预期
            count++;   //  每有一组符合，就加1
        }
    }
    return count;
}

int main()
{
    int i, n;
    cin >> n;
    int *a = new int[n + 1];

    for (i = 1; i <= n; ++i)
    {
        cin >> a[i];
    }
    for (i = 1; i <= n; ++i)
    {
        cout << "Case #" << i << ": " << function(a[i]) << endl;
    }
    system("pause");
    return 0;
}

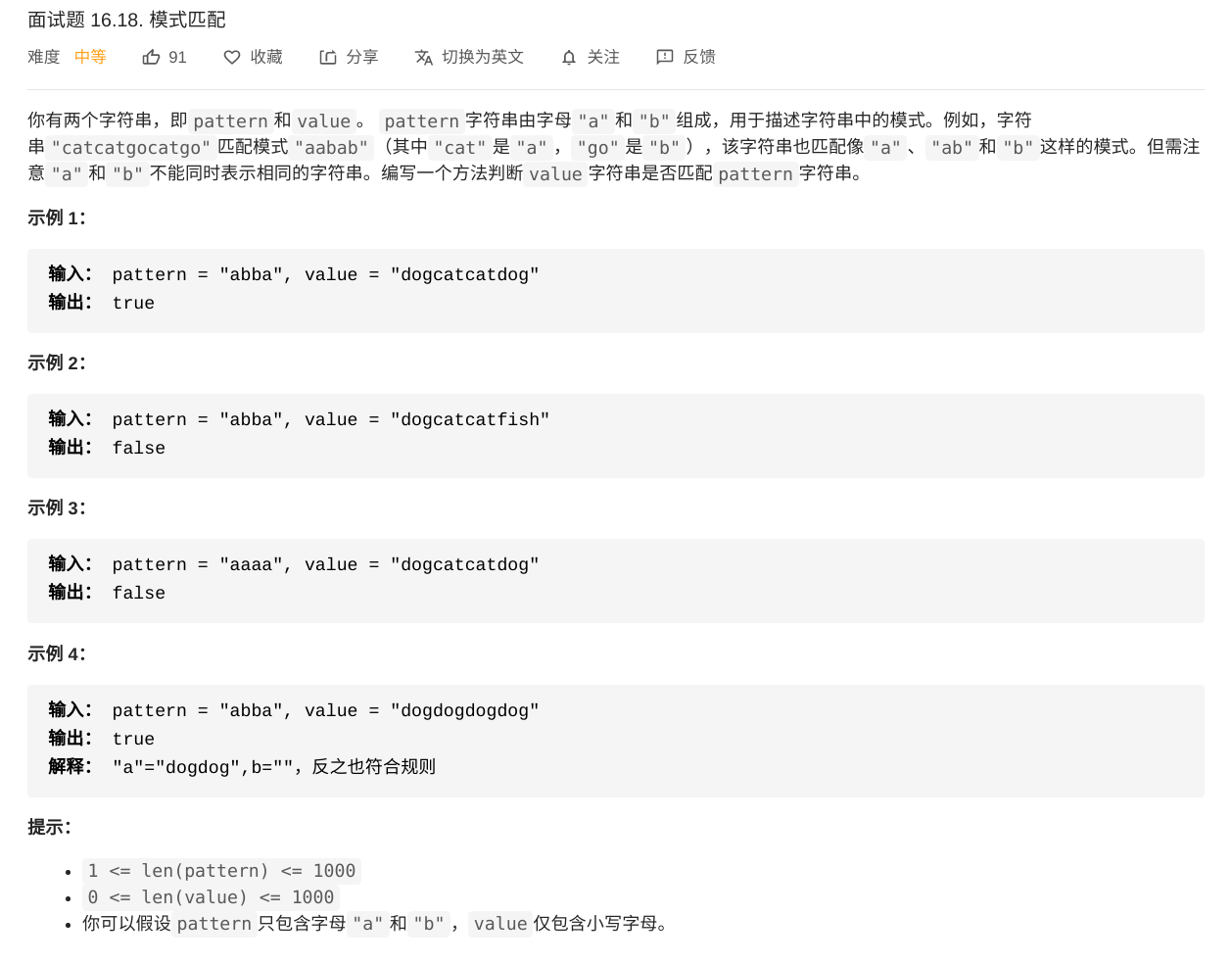
面试题 16.18. 模式匹配

image.png

class Solution {
public:
    bool patternMatching(string pattern, string value) {
        int count_a =0,count_b=0;
        int len_p =pattern.size(),len_v =value.size();
        // 特殊情况处理
        if(!len_p) return false;
        // 统计a 和b 的个数
        for(int i=0;i<len_p;i++){
            if(pattern[i]=='a') count_a++;
            else count_b++;
        }

        // a b 所代表的字符串的最大长度
        int maxlen_a=0,maxlen_b=0;// 防止为0
        if(count_a) maxlen_a = len_v/count_a;
        if(count_b) maxlen_b = len_v/count_b; 

        //枚举,凑出a b 的长度
        for(int i=0;i<=maxlen_a;i++){
            for(int j=0;j<=maxlen_b;j++){
                if(i*count_a+j*count_b==len_v){ // i j 分别代表子串的长度
                    string s_a="#",s_b="#";
                    int k_value=0;// 指向value 的指针
                    for(int k=0;k<len_p;k++){
                         if(pattern[k]=='a'){
                            if(s_a=="#") s_a = value.substr(k_value,i);//第一次 给赋值;
                            else if(s_a!=value.substr(k_value,i)) break;
                            k_value+=i;
                        }
                        else{
                            if(s_b=="#") s_b= value.substr(k_value,j);
                            else if(s_b!=value.substr(k_value,j)) break;
                            k_value+=j;
                        }
                    }
                    if((k_value==len_v)&&(s_a!=s_b)) return true;
                }
            }
        }
        return false;
    }
};

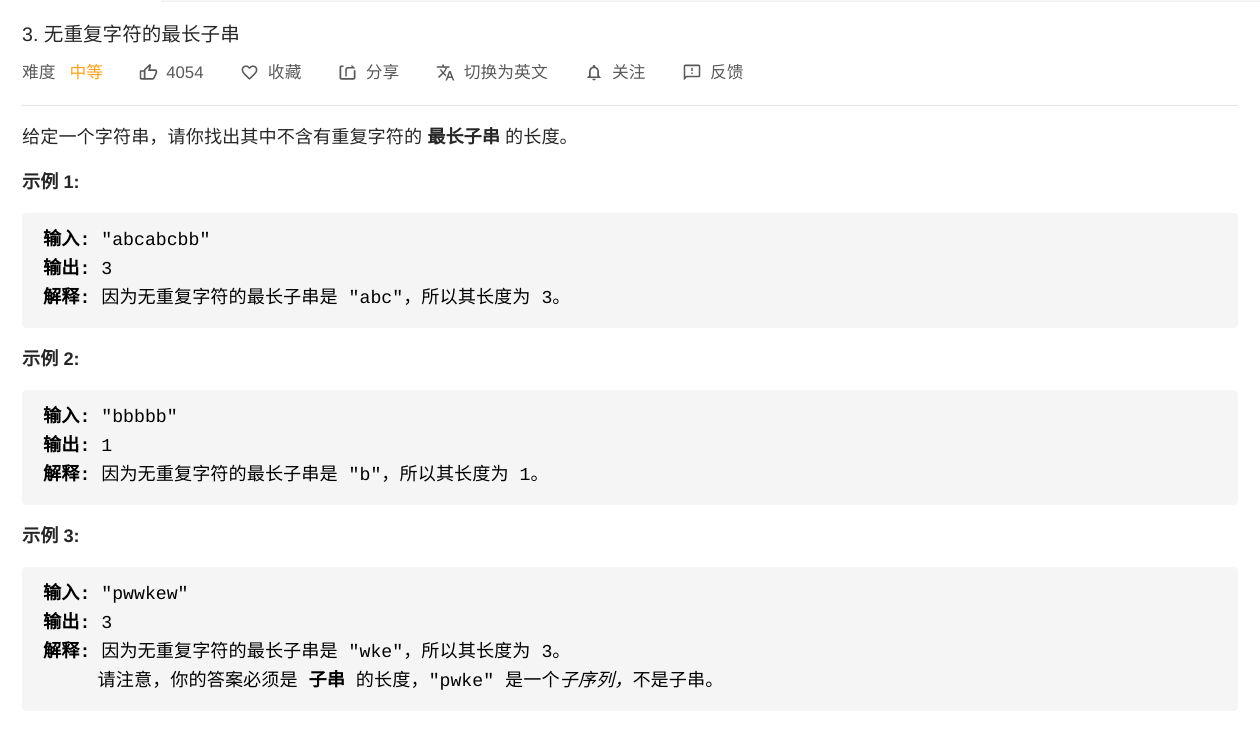
3. 无重复字符的最长子串

image.png

// 双指针算法  哈希表
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int res = 0;
        unordered_map<char,int> hashmap;
        for(int i=0,j=0;i<s.size();i++){
            hashmap[s[i]]++;
            while(hashmap[s[i]]>1) hashmap[s[j]]--,j++;
            res = max(res,i-j+1);
        }
        return res;
    }
};

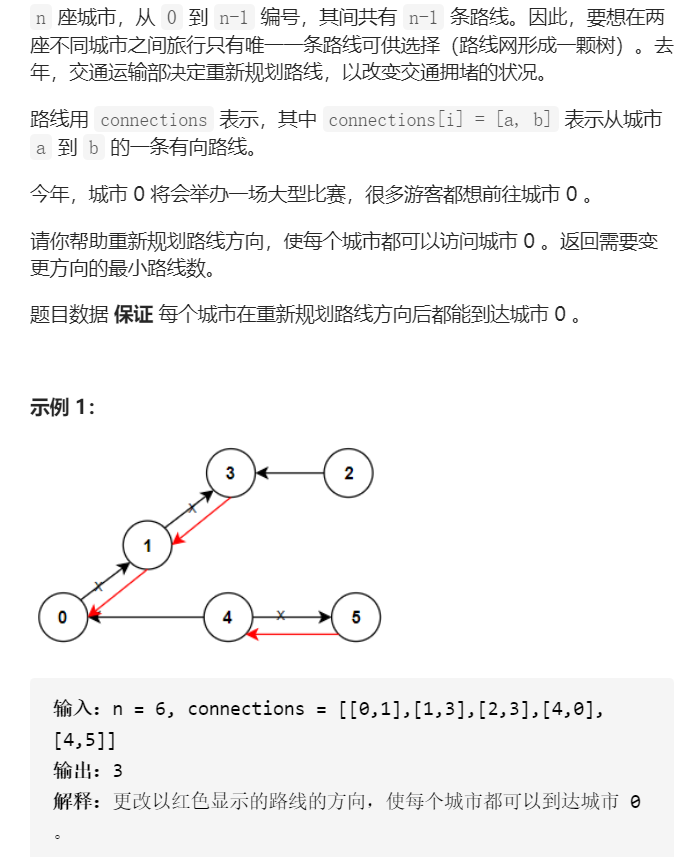
1466. 重新规划路线

image.png

以相反的顺序打印字符串

void printReverse(const char *str) {
  if (!*str)
    return;
  printReverse(str + 1);
  putchar(*str);
}

反转字符串
编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

class Solution {
public:    
    void reverseString(vector<char>& s) {
        if(s.empty()) return;
        dfs(s,0,s.size()-1);
    }
    void dfs(vector<char>& s,int i,int j){
        if(i>=j) return ;
        swap(s[i],s[j]);
        dfs(s,i+1,j-1);  
    }
};

24. 两两交换链表中的节点

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

思路：
每次独立的事件中：

  • 判断返回条件
  • 返回头节点
  • 交换节点
    class Solution {
public:
  ListNode* swapPairs(ListNode* head) {
      if(head==NULL||head->next==NULL) return head ;
      ListNode* tmp=head->next;
      head->next=swapPairs(head->next->next);
      tmp->next=head;
      return tmp;
  }
};
// 时间复杂度 O(n),空间复杂度 O(n)