分配律

    笔记二：逻辑代数 - 图1
    笔记二：逻辑代数 - 图2

    吸收律
    笔记二：逻辑代数 - 图3
    笔记二：逻辑代数 - 图4
    笔记二：逻辑代数 - 图5
    笔记二：逻辑代数 - 图6
    笔记二：逻辑代数 - 图7

    德·摩根定律

    笔记二：逻辑代数 - 图8
    笔记二：逻辑代数 - 图9

    逻辑代数的基本定理

    代入定理

    在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式代入式中所有A的位置，等式仍然成立。

    变量A仅有0和1两种可能的状态，而另一个逻辑式的取值也仅有0和1两种

    反演定理

    对于任意一个逻辑式Y，若将其中所有的“·”换成“+”，将“+”换成“·”，0换成1，1换成0，原变量换成反变量，反变量换成原变量，则得到笔记二：逻辑代数 - 图10

    三个互换：

    • 01互换
    • 与或互换
    • 原反变量互换

    两个不变：

    • 运算优先次序不变：先括号，其次乘，最后加
    • 不属于单个变量上的反号不变

    运算优先级：括号、反号 > 与（逻辑乘） > 异或、同或 > 或（逻辑加）
    德·摩根定律拆分时从优先级最低的运算符起拆。

    对偶定理

    若两逻辑式相等，则它们的对偶式也相等。

    对偶式：对于任意一个逻辑式Y，若将其中所有的“·”换成“+”，将“+”换成“·”，0换成1，1换成0，，则得到Y的对偶式笔记二：逻辑代数 - 图11

    两个互换：

    • 01互换
    • 与或互换

    逻辑函数的5类基本形式：

    • 与或式
    • 与非-与非式
    • 与或非式
    • 或与式
    • 或非-或非式

    笔记二：逻辑代数 - 图12 例：最简与或式笔记二：逻辑代数 - 图13化为其他形式

    笔记二：逻辑代数 - 图14
    II_KV9VE]EKK3K_TE%Z0Y~1.png
    与非-与非式：与或式两次取反，用德·摩根定律展开一层

    笔记二：逻辑代数 - 图16
    ![H%URGC)%NF(%X$8%GFZ$J6.png

    与或非式：先求出反函数的与或式，再取反一次，不处理即可

    笔记二：逻辑代数 - 图17

    笔记二：逻辑代数 - 图18
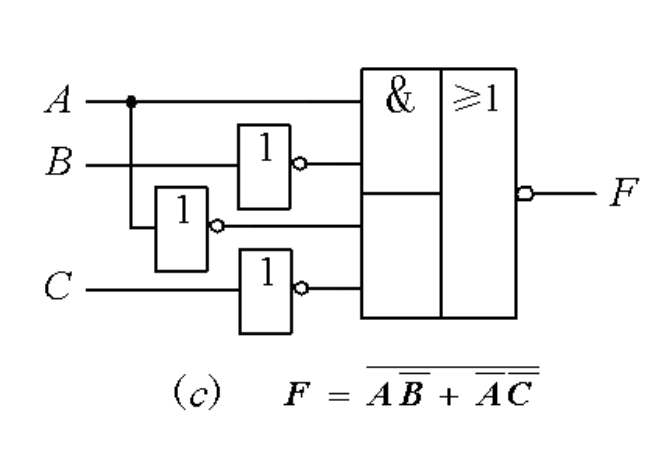
    (RVB_I0YB_L06B~4%FPD3M1.png

    或与式：与或非式用德·摩根定律展开两层

    笔记二：逻辑代数 - 图20
    _9KREB{]Q05JR]S5SY`~S3W.png

    或非-或非式：或与式两次取反，用德·摩根定律展开一层

    笔记二：逻辑代数 - 图22
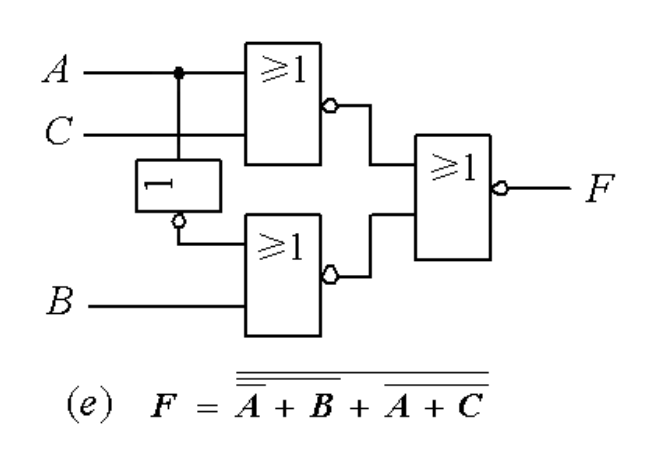
    6@70R6D~8R%@S6OUBT2)V$Q.png
    逻辑电路化简原则：三少一可靠

    • 逻辑电路所用的门要少
    • 每个门的输入端要少
    • 逻辑电路所用的级数要少
    • 逻辑电路能更可靠地工作

    逻辑函数的表示工具：

    • 真值表
    • 逻辑表达式
    • 卡诺图
    • 逻辑电路图
    • 波形图

    卡诺图

    卡诺图上的一个方格就对应着逻辑函数的一个最小项

    最小项笔记二：逻辑代数 - 图24真值表上的一行笔记二：逻辑代数 - 图25卡诺图上的一个方格：对应着一组确定的输入条件组合

    真值表笔记二：逻辑代数 - 图26标准与或式：准确地表达了一个逻辑命题的功能

    卡诺图的化简原理笔记二：逻辑代数 - 图27吸收定律：两项变一项，谁变吸收谁

    逻辑函数的逻辑相邻关系笔记二：逻辑代数 - 图28卡诺图上的几何相邻关系

    超过4个变量，卡诺图的几何相邻关系就需要引入对称位才可以反映逻辑相邻关系，因此卡诺图一般只用于3或4个变量的逻辑函数化简