姓名：Far_Rainbow
    学号： 202505000X
    专业： 软件工程
    年级：2020级

    实验名称：实验2 基于顺序表的非递减有序表的合并

    实验内容：

    （1）实验目的
    通过该实验，深入理解顺序表的逻辑结构、物理结构等概念，掌握顺序表基本操作的编程实现，注意顺序表插入、删除等操作过程中数据元素的移动现象，培养学生编写程序时，要考虑程序的健壮性，全面考虑问题，熟练掌握通过函数参数返回函数结果的办法。

    （2）实验内容
    编程实现顺序表下教材第二章定义的线性表的基本操作，并根据已经实现的基本操作，实现两个非递减有序的线性表的合并，注意，合并时，如果有重复的元素(一个表内部的重复元素和两个表之间的重复元素)，请保留一个。

    （3）实验要求

    • 求前驱是指，输入一个元素值（而不是位置），求该元素在顺序表中的直接前驱元素值。求后继是指：输入一个元素值（而不是位置），求该元素在顺序表中的直接后继元素值；
    • 为了方便修改数据元素的类型，请使用类型重定义，可以方便修改线性表中的数据元素的类型；
    • 大部分函数的返回结果应是函数执行是否成功的一种状态，执行成功了，才返回具体的结果值；
    • 对每个功能进行测试时，要求把不合法的情况也测试一下。具体见下面的测试用例；
    • 采用菜单形式对应各个操作，使其编成一个完整的小软件，参考界面如下。注意：程序运行过程中菜单不要做成刷屏的效果，测试过的数据不要清除，这样方便截图和查看。

    （4）验收/测试用例
    通过菜单调用各个操作，测试点：

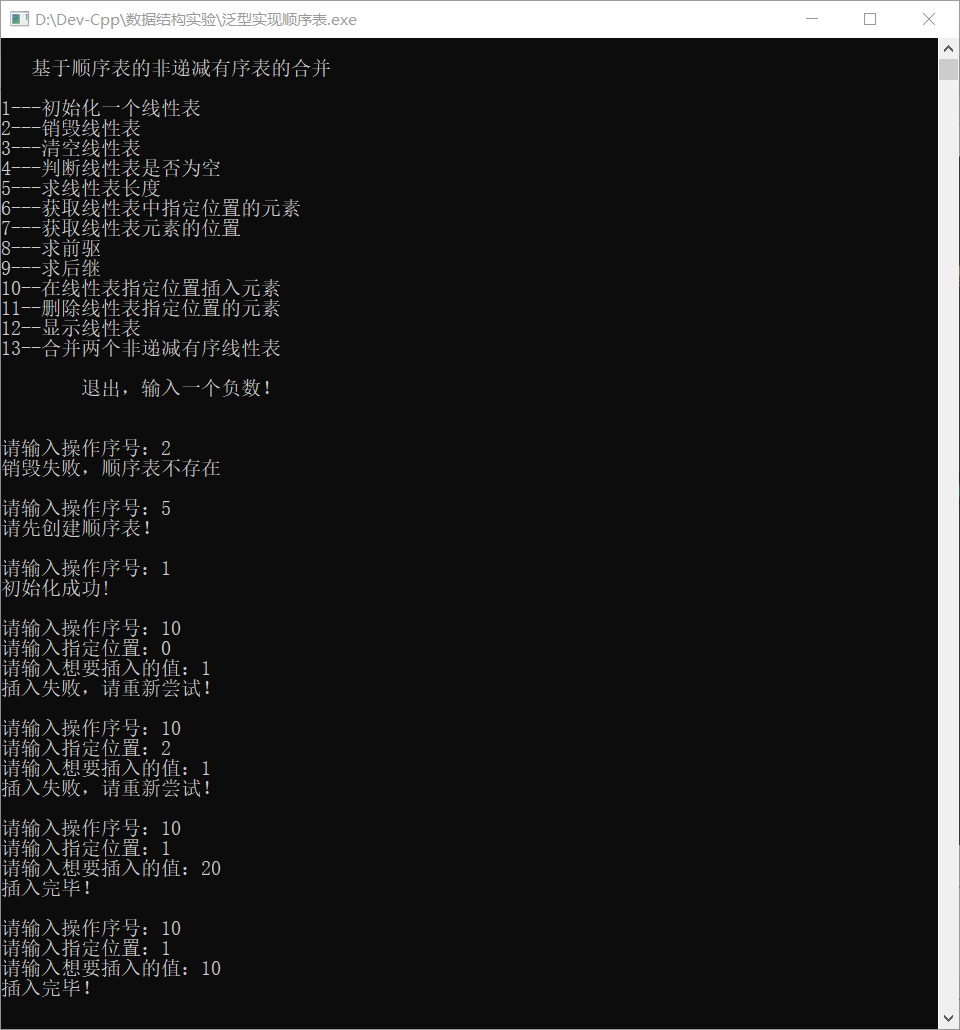
    • 没有初始化前进行其他操作，程序是否能控制住；即，如果没有初始化线性表，其他的功能是无法正常进行的，如果选择进行其他操作，要提示先进行初始化；
    • 先选择菜单1，初始化一个顺序表（初始化顺序表，是指初始化一个空的线性表，里面的元素个数是0）；
    • 选择菜单10，插入数据(位置， 数据)，要测插入位置不合法的情况（0,1）、（2,1），正确插入3个数据（1，20）、（1，10）、（3,30）；
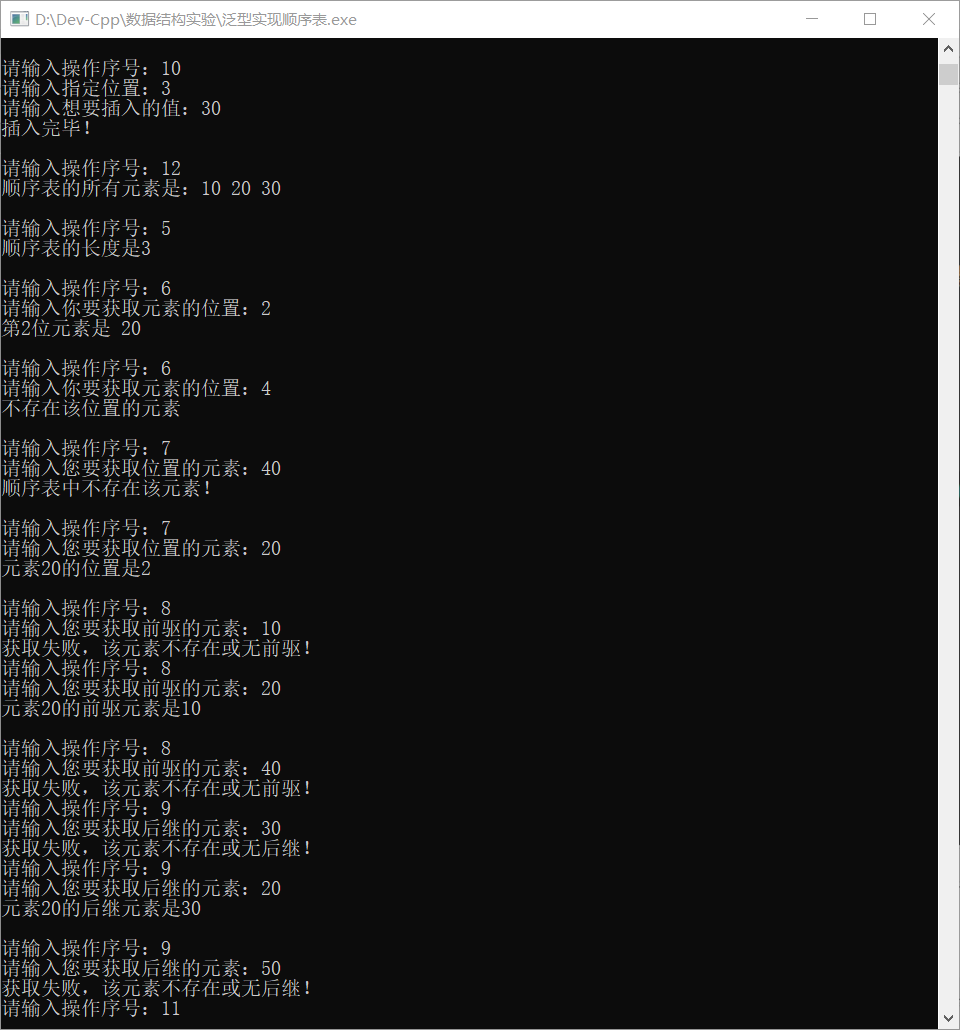
    • 显示顺序表中的数据，屏幕输出10， 20， 30；
    • 判空，屏幕输出顺序表非空；
    • 输出顺序表长度，屏幕输出3；
    • 获取指定位置元素，要测指定位置在【1，3】范围之外的情况和之内的情况；
    • 定位，输入：40， 输出：不存在，输入20，输出位置为2；
    • 求直接前驱，要测求第一个元素的前驱、不存在顺序表中的元素的直接前驱，其他元素的直接前驱；输入10，输出：第一个元素没有前驱，输入20，输出前驱是10，输入40，输出该元素不存在；
    • 求直接后继，要测最后一个元素的后继、不存在顺序表中的元素的直接后继，其他元素的直接后继；同上求前驱；
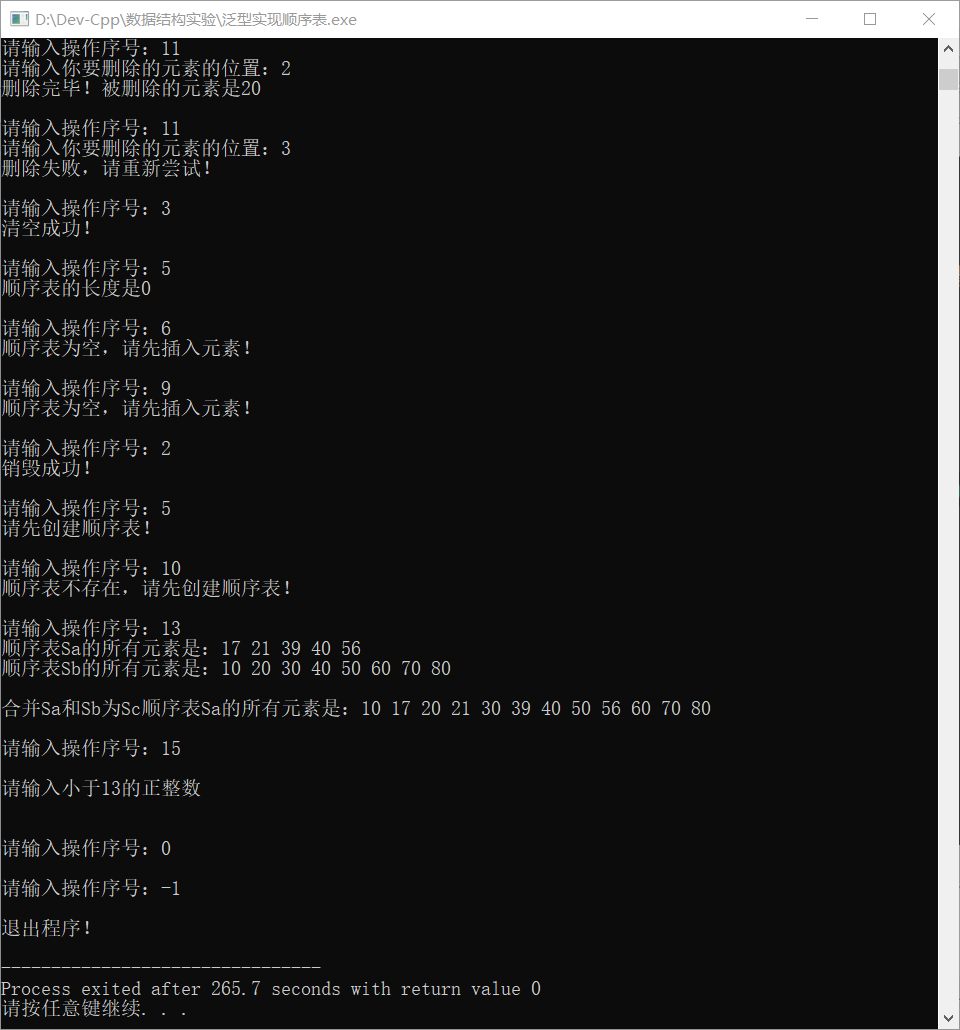
    • 删除，要测位置在【1，3】范围之外的情况和之内的情况；
    • 清空操作后再测长度，判断是否为空；清空后，测试菜单6到11的功能，看是否能够正确提示。
    • 销毁顺序表，销毁线性表之后还能不能做插入，删除等操作，如果选其他操作，就要提示线性表已经销毁不存在；
    • 测试合并操作，第一个线性表中的元素是（2,3,3,4，5），第二个线性表中的内容是（1,4,5，6,6,7），合并后的结果，请输出。

    实验类型：验证性

    实验的重难点：顺序表的定义和实现，销毁和清空的区别、 两个非递减有序表的去重合并

    实验环境：TDM-GCC 4.9.2 64-bit

    实验步骤及完成任务情况：

    一、设计思想

    1. 采用模板实现泛型编程，可创建任意数据类型的顺序表；
    2. 采用动态内存分配的方式管理顺序表的容量，在顺序表内存空间不够时通过expend()函数扩容；
    3. 体会顺序表插入删除时间复杂度都是实验2 基于顺序表的非递减有序表的合并 - 图1#card=math&code=O%28n%29&id=I9Snm)的特点

    二、主要源代码

    1. #include <iostream>
    2. #define SEQUENCESIZE 1000
    3. #define SEQUENCEINCREMENT 500
    4. using std::cin;
    5. using std::cout;
    6. using std::endl;
    8. template <typename T> class Sequence {
    9. private:
    10.     T* elem;
    11.     int _length;
    12.     int _capacity;
    13.     void expand();
    15. public:
    16.     Sequence() {elem = NULL; _length = 0; }
    17.     Sequence(T arr[], int size) 
    18.     {init(); for (int i = 0; i < size; ++ i) elem[i] = arr[i]; _length = size; }
    19.     ~Sequence() {destroy(); }
    20.     void init();
    21.     void destroy();
    22.     void clear() {_length = 0; }
    23.     T operator[](int pos) {return elem[pos]; }
    24.     bool isempty() const {return _length > 0 ? 0 : 1; }
    25.     bool exist() const {return elem > 0 ? 1 : 0; }
    26.     int getlength() const {return _length; }
    27.     bool getelem(int pos, T& e) const 
    28.     {if(pos > _length + 1 || pos < 1) return false; e = elem[pos-1]; return true; }
    29.     int elemlocate(T const& e) const 
    30.     {for(int i = 0; i < _length; ++ i) if(elem[i] == e) return i+1; return -1;}
    31.     bool priorelem(T const& e, int& pos);
    32.     bool nextelem(T const& e, int& pos);
    33.     bool insert(T const& e, int pos);
    34.     bool remove(T& e, int pos);
    35.     void push(T const& e);
    36.     T pop() {-- _length; return _length + 1; }
    37.     void traverse() const 
    38.     {for(int i = 0; i < _length; i ++) cout<<elem[i]<<' '; }
    39.     void merge(Sequence<T>& Sa, Sequence<T>& Sb);
    40. };
    42. template <typename T> void Sequence<T>::init()
    43. {
    44.     elem = new T[SEQUENCESIZE];
    45.     _capacity = SEQUENCESIZE; 
    46. }
    48. template <typename T> void Sequence<T>::destroy()
    49. {
    50.     if (!exist())    return;
    51.     delete[] elem;
    52.     elem = NULL;
    53.     _length = 0;
    54.     _capacity = 0;
    55. }
    57. template <typename T> void Sequence<T>::expand()
    58. {
    59.     T* newelem = new T[_capacity+SEQUENCEINCREMENT];
    60.     for(int i = 0; i < _length; ++ i)    newelem[i] = elem[i];
    61.     delete[] elem;
    62.     elem = newelem;
    63. }
    65. template <typename T> bool Sequence<T>::priorelem(T const& e, int& pos)
    66. {
    67.     int i = elemlocate(e);
    68.     if (i < 2 || i > _length)    return false;
    69.     pos = i - 1;
    70.     return true;
    71. }
    73. template <typename T> bool Sequence<T>::nextelem(T const& e, int& pos)
    74. {
    75.     int i = elemlocate(e);
    76.     if (i < 1 || i > _length - 1)    return false;
    77.     pos = i + 1;
    78.     return true;
    79. }
    81. template <typename T> bool Sequence<T>::insert(T const& e, int pos) 
    82. {
    83.     if (pos < 1 || pos > _length + 1)    return false;
    84.     if (_capacity < _length + 1)    expand();
    85.     for(int j = _length - 1; j >= pos - 1; -- j) // 最开始写成j>i-1了，debug了好几个小时，血的教训 
    86.         elem[j+1] = elem[j];
    87.     elem[pos-1] = e;
    88.     ++ _length;
    89.     return true;
    90. }
    92. template <typename T> bool Sequence<T>::remove(T& e, int pos)
    93. {
    94.     if(pos < 1 || pos > _length)    return false;
    95.     e = elem[pos-1];
    96.     for(int j = pos - 1; j < _length - 1; ++ j)
    97.         elem[j] = elem[j+1];
    98.     -- _length;
    99.     return true;
    100. } 
    102. template <typename T> void Sequence<T>::push(T const& e)
    103. {
    104.     if (_capacity < _length + 1)    expand();
    105.     elem[_length] = e;
    106.     ++ _length;
    107. } 
    109. template <typename T> void Sequence<T>::merge(Sequence<T>& Sa, Sequence<T>& Sb)
    110. {
    111.     int i = 0, j = 0, k = 0;
    112.     while(i < Sa._length && j < Sb._length) {  //不能 <= ，否则会数组下标越界 
    113.         if (Sa[i] < Sb[j])    elem[k++] = Sa[i++]; 
    114.         else if (Sa[i] > Sb[j])    elem[k++] = Sb[j++];
    115.         else if (Sa[i] == Sb[j++])    elem[k++] = Sa[i++]; // 去重 
    116.     } 
    117.     while (i < Sa._length)    elem[k++] = Sa[i++];
    118.     while (j < Sb._length) elem[k++] = Sb[j++];
    119.     _length = k; 
    120. }
    122. int main()
    123. {
    124.     cout<<"\n   基于顺序表的非递减有序表的合并\n\n";
    125.     cout<<"1---初始化一个线性表\n";
    126.     cout<<"2---销毁线性表\n";
    127.     cout<<"3---清空线性表\n";
    128.     cout<<"4---判断线性表是否为空\n";
    129.     cout<<"5---求线性表长度\n";
    130.     cout<<"6---获取线性表中指定位置的元素\n";
    131.     cout<<"7---获取线性表元素的位置\n";
    132.     cout<<"8---求前驱\n";
    133.     cout<<"9---求后继\n";
    134.     cout<<"10--在线性表指定位置插入元素\n";
    135.     cout<<"11--删除线性表指定位置的元素\n";
    136.     cout<<"12--显示线性表\n";
    137.     cout<<"13--合并两个非递减有序线性表\n"; 
    138.     cout<<"\n\t退出，输入一个负数！\n\n";
    139.     Sequence<int> Se;
    140.     while(true)
    141.     {
    142.         int myOption;
    143.         cout<<"\n请输入操作序号：";
    144.         cin>>myOption;
    145.         switch(myOption){
    146.             case 1:{
    147.                 if(Se.exist()){
    148.                     cout<<"初始化失败，顺序表已存在！\n";
    149.                     break; 
    150.                 }
    151.                 Se.init();
    152.                 cout<<"初始化成功!\n";
    153.                 break;
    154.             }
    155.             case 2:{
    156.                 if (!Se.exist()){
    157.                     cout<<"销毁失败，顺序表不存在\n";
    158.                     break; 
    159.                 }
    160.                 Se.destroy();
    161.                 cout<<"销毁成功！\n";
    162.                 break;
    163.             } 
    164.             case 3:{
    165.                 if (!Se.exist()){
    166.                     cout<<"清空失败，顺序表不存在\n";
    167.                     break; 
    168.                 }
    169.                 if (Se.isempty()) ; 
    170.                 else    Se.clear();
    171.                 cout<<"清空成功！\n"; 
    172.                 break;
    173.             }
    174.             case 4:{
    175.                 if (!Se.exist()){
    176.                     cout<<"判空失败，顺序表不存在\n";
    177.                     break; 
    178.                 }
    179.                 if (Se.isempty())    cout<<"顺序表为空！\n";
    180.                 else    cout<<"顺序表非空！\n"; 
    181.                 break;
    182.             }
    183.             case 5:{
    184.                 if (!Se.exist()){
    185.                     cout<<"请先创建顺序表！\n";
    186.                     break; 
    187.                 }
    188.                 cout<<"顺序表的长度是"<<Se.getlength()<<endl; 
    189.                 break;
    190.             }
    191.             case 6:{
    192.                 if (!Se.exist()){
    193.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    194.                     break; 
    195.                 }
    196.                 if (Se.isempty()){
    197.                     cout<<"顺序表为空，请先插入元素！\n";
    198.                     break;
    199.                 }
    200.                 cout<<"请输入你要获取元素的位置：";
    201.                 int pos, e;
    202.                 cin>>pos;
    203.                 if (!Se.getelem(pos, e)) {
    204.                     cout<<"不存在该位置的元素\n";
    205.                     break;
    206.                 }
    207.                 cout<<"第"<<pos<<"位元素是 "<<e<<endl; 
    208.                 break;
    209.             }
    210.             case 7:{
    211.                 if (!Se.exist()){
    212.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    213.                     break; 
    214.                 }
    215.                 if (Se.isempty()){
    216.                     cout<<"顺序表为空，请先插入元素！\n";
    217.                     break;
    218.                 }
    219.                 cout<<"请输入您要获取位置的元素：";
    220.                 int e;
    221.                 cin>>e;
    222.                 if (!Se.elemlocate(e)){
    223.                     cout<<"顺序表中不存在该元素！\n";
    224.                     break;
    225.                 }
    226.                 cout<<"元素"<<e<<"的位置是"<<Se.elemlocate(e)<<endl; 
    227.                 break;
    228.             }
    229.             case 8:{
    230.                 if (!Se.exist()){
    231.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    232.                     break; 
    233.                 }
    234.                 if (Se.isempty()){
    235.                     cout<<"顺序表为空，请先插入元素！\n";
    236.                     break;
    237.                 }
    238.                 cout<<"请输入您要获取前驱的元素：";
    239.                 int pos, e;
    240.                 cin>>e;
    241.                 if (!Se.priorelem(e, pos)){
    242.                     cout<<"获取失败，该元素不存在或无前驱！";
    243.                     break; 
    244.                 }
    245.                 cout<<"元素"<<e<<"的前驱元素是"<<Se[pos-1]<<endl;
    246.                 break;
    247.             }
    248.             case 9:{
    249.                 if (!Se.exist()){
    250.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    251.                     break; 
    252.                 }
    253.                 if (Se.isempty()){
    254.                     cout<<"顺序表为空，请先插入元素！\n";
    255.                     break;
    256.                 }
    257.                 cout<<"请输入您要获取后继的元素：";
    258.                 int pos, e;
    259.                 cin>>e;
    260.                 if (!Se.nextelem(e, pos)){
    261.                     cout<<"获取失败，该元素不存在或无后继！";
    262.                     break; 
    263.                 }
    264.                 cout<<"元素"<<e<<"的后继元素是"<<Se[pos-1]<<endl;
    265.                 break;
    266.             }
    267.             case 10:{
    268.                 if (!Se.exist()){
    269.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    270.                     break; 
    271.                 }
    272.                 cout<<"请输入指定位置：";
    273.                 int pos;
    274.                 cin>>pos;
    275.                 cout<<"请输入想要插入的值：";
    276.                 int e;
    277.                 cin>>e;
    278.                 if (!Se.insert(e, pos)){
    279.                     cout<<"插入失败，请重新尝试！\n";
    280.                     break;
    281.                 }
    282.                 else    cout<<"插入完毕！\n";
    283.                 break;
    284.             }
    285.             case 11:{
    286.                 if (!Se.exist()){
    287.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    288.                     break; 
    289.                 }
    290.                 if (Se.isempty()){
    291.                     cout<<"顺序表为空！\n";
    292.                     break;
    293.                 }
    294.                 cout<<"请输入你要删除的元素的位置：";
    295.                 int pos;
    296.                 cin>>pos;
    297.                 int e;
    298.                 if (!Se.remove(e, pos)){
    299.                     cout<<"删除失败，请重新尝试！\n";
    300.                     break;
    301.                 }
    302.                 else    cout<<"删除完毕！"<<"被删除的元素是"<<e<<endl;;
    303.                 break;
    304.             }
    305.             case 12:{
    306.                 if (!Se.exist()){
    307.                     cout<<"顺序表不存在，请先创建顺序表！\n";
    308.                     break; 
    309.                 }
    310.                 if (Se.isempty()){
    311.                     cout<<"顺序表为空！\n";
    312.                     break;
    313.                 }
    314.                 cout<<"顺序表的所有元素是：";
    315.                 Se.traverse();
    316.                 cout<<endl;
    317.                 break;
    318.             } 
    319.             case 13:{
    320.                 int a[5] = {17, 21, 39, 40, 56};
    321.                 int b[8] = {10, 20, 30, 40, 50, 60, 70, 80};
    322.                 Sequence<int> Sa(a, 5);
    323.                 Sequence<int> Sb(b, 8);
    324.                 cout<<"顺序表Sa的所有元素是：";
    325.                 Sa.traverse();
    326.                 cout<<endl;
    327.                 cout<<"顺序表Sb的所有元素是：";
    328.                 Sb.traverse();
    329.                 cout<<endl;
    330.                 Sequence<int> Sc;
    331.                 Sc.init();
    332.                 Sc.merge(Sa, Sb);
    333.                 cout<<"\n合并Sa和Sb为Sc";
    334.                 cout<<"顺序表Sa的所有元素是：";
    335.                 Sc.traverse();
    336.                 cout<<endl;
    337.                 break;
    338.             }
    339.         }
    340.         if(myOption >13)    cout<<"\n请输入小于13的正整数\n\n";
    341.         if(myOption < 0){
    342.             cout<<"\n退出程序！\n";
    343.             break;
    344.         }
    345.     } 
    346.     return 0;
    347. }

    实验结果：
    实验2 基于顺序表的非递减有序表的合并 - 图2
    实验2 基于顺序表的非递减有序表的合并 - 图3
    实验2 基于顺序表的非递减有序表的合并 - 图4