一、冒泡排序
时间复杂度:O(n2)
空间复杂度:O(1)
排序稳定性:稳定
public class Main {public static void main(String[] args) {int[] nums = new int[]{9,2,7,6,4,8,1,10};bubbleSort(nums);}public static int[] bubbleSort(int[] nums){int len = nums.length;boolean flag = true;for (int i = 0; i < len && flag; i ++) {//遍历次数flag = false;for (int j = 0;j < len-1;j ++) {if(nums[j] > nums[j + 1]){//每次相邻两个比较,交换相邻两个数,大的往后int temp = nums[j];nums[j] = nums[j+1];nums[j+1] = temp;//如果这一次遍历做了交换,后面还要遍历。// 如果这次没有过数字交换,说明数组顺序排好了,后面还有次数都不用执行flag = true;}}for (int num : nums) {System.out.print(num+" ");}System.out.println();}return nums;}}输出:2 7 6 4 8 1 9 102 6 4 7 1 8 9 102 4 6 1 7 8 9 102 4 1 6 7 8 9 102 1 4 6 7 8 9 101 2 4 6 7 8 9 101 2 4 6 7 8 9 10
优化代码:加一个flag,判断上一轮有没有数据交换。
二、简单选择排序
时间复杂度:O(n2)
空间复杂度:O(1)
稳定性:不稳定
public class Main {public static void main(String[] args) {int[] nums = new int[]{9,2,7,6,4,8,1,10,12};selectionSort(nums);}public static int[] selectionSort(int[] nums){int len = nums.length;for (int i = 0; i < len; i++) {int minIndex = i;for (int j = i+1;j < len; j++) {//从未排序中找出最小值if(nums[minIndex] > nums[j]) {minIndex = j;}}//将最小值放在排序序列最后端int temp = nums[minIndex];nums[minIndex] = nums[i];nums[i] = temp;for (int num : nums) {System.out.print(num+" ");}System.out.println();}return nums;}}输出:1 2 7 6 4 8 9 10 121 2 7 6 4 8 9 10 121 2 4 6 7 8 9 10 121 2 4 6 7 8 9 10 121 2 4 6 7 8 9 10 121 2 4 6 7 8 9 10 121 2 4 6 7 8 9 10 121 2 4 6 7 8 9 10 121 2 4 6 7 8 9 10 12
选择排序的优化为,在找最小值的同时找出最大值。一个循环后,最小值放在左边,最大值放在右边。但是这种方法,并没有减少时间复杂度。
三、直接插入排序
时间复杂度:O(n2)
空间复杂度:O(1)
稳定性:稳定
public class Main {public static void main(String[] args) {int[] nums = new int[]{9, 2, 7, 6, 4, 8, 1, 10, 12};directInsertionSort(nums);}public static int[] directInsertionSort(int[] nums) {int len = nums.length;for (int i = 1; i < len; i++) {//从第二个元素开始寻找插入元素的位置int position = i;for (int j = i - 1; j >= 0; j--) {//遍历已经排好的位置if (nums[i] < nums[j]) {position = j;//找出序列中比nums[i]大的最小值}}/*优化这部分为冒泡内循环*/int temp = nums[i];//暂存需要插入的元素//往后移动for (int k = i; k > position; k--) {nums[k] = nums[k - 1];}nums[position] = temp;//在目标位置插入对的元素for (int m = 0; m < len; m++) {System.out.print(nums[m] + " ");}System.out.println();}return nums;}}
优化,将往后移动那部分代码改为,从后往前交换值,直到相应的位置。然后记录发生交换的次数,如果没有发生交换这个序列基本有序。(这相当于同时做了冒泡的内层)

希尔排序(跨度分组排序)
基本有序:相隔一定的跨度,的子序列是有序的。
选择不同的跨度分组,使分组内的子序列是有序的。组内排序属于直接插入排序
时间复杂度:O(NlogN)~O(N2)
空间复杂度:
稳定性:不稳定
跨度逐渐减小,进行直接插入排序,直到跨度为一
堆排序
- 堆是具有下列性质的完全二叉树:每个节点的值都大于或等于其左右孩子结点的值称为大顶堆,或者每个节点的值都小于或等于其左右孩子结点的值,称为小顶堆。
- 构造大顶堆:从按照层序遍历构造的二叉树开始,将每棵子树的根结点与叶子结点中的最大值交换。直到每棵子树的根节点最大(即大顶堆)。
- 堆排序 :(大堆排序)先构造一个大顶堆,将顶堆的根节点移走,(实质是与末尾元素做交换)。然后又构造一个大顶堆,将顶堆的根节点移走(实质是与存上一个根节点的位置前一个元素做交换)。重复,直到所有的元素移走,排序完成。
- 复杂度:O(nlogn)

先构建大顶推,将根节点和末尾的元素交换,在构建大顶堆,再将根节点与末尾的元素交换。重复操作,直到所大顶堆中不含元素。
快速排序
时间复杂度:O(nlogn) 平均
快速排序:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到,整个序列有序。
快速排序的基本思想。
1.先从数组中找一个基准数(第一个元素设为轴心点)
2.让其他比它大的元素移动到数列一边,比他小的元素移动到数列另一边,从而把数组拆解成两个部分。
3.再对左右区间重复第二步,直到各区间只有一个数。

基准数:3,38,19,26,27,46,47,50
归并排序
- 该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
- 归并排序:先拆分为单个,然后选择两组数组中的最小值,加入组合数组。

类似二叉树的出栈排序
下图可能先后有问题,原理上图清晰。
计数排序
基数排序
第一步:按数组当中元素的最低有效位,个位,进行计数排序
第二步:按数组当中元素的次最低有效位,十位数,进行计数排序:
总结
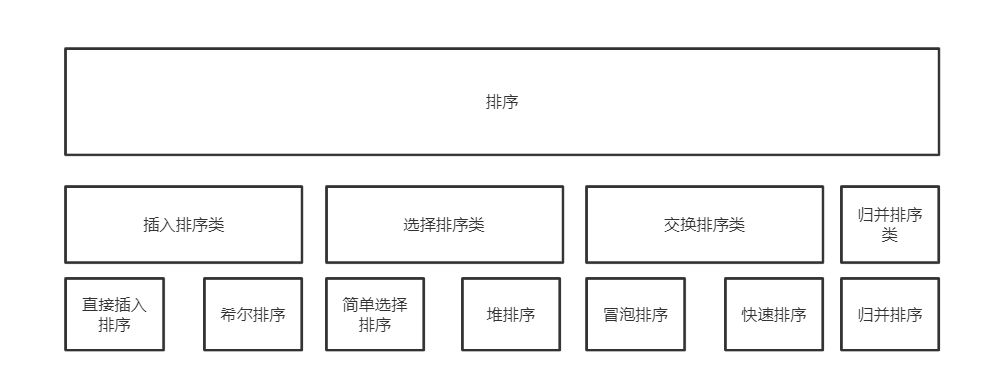
简单算法:冒泡,简单选择,直接插入
改进算法:希尔,堆,快速,归并
01、排序算法对比
| 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡 | O(N2) | O(1) | 稳定 |
| 简单选择 | O(N2) | O(1) | 不稳定 |
| 直接插入 | O(N2) | O(1) | 稳定 |
| 希尔排序 | O(NlogN)~O(N2) | O(1) | 不稳定 |
| 堆排序 | O(NlogN) | O(1) | 不稳定 |
| 快速排序 | O(NlogN) | O(NlogN)~O(n) | 不稳定 |
| 归并排序 | O(NlogN) | O(n) | 稳定 |
02、排序的一些概念
1、排序的稳定性
假设ri=rj,且在排序前ri领先于rj,如果排序后ri仍领先rj,则称排序的方法是稳定的。
破坏了原来的相对位置。
2、内排序和外排序
- 内排序:在排序的过程中,待排序的所有记录都被放置在内存中。
- 外排序:由于排序的记录个数太多,不能同时放在内存中,整个过程需要内外存之间多次交换数据才能进行。
对内排序来说,算法的排序性能主要受3个因素影响:
- 时间性能
- 辅助空间
- 算法复杂性


