全排列

链接：https://leetcode-cn.com/problems/permutations/

解题思路：回溯

当题目中有“所有组合”，“全排列”这样的字眼时，我们就应该在第一时间想到回溯算法。

初始化：

• int[] nums 为给定的输入数组
• int cur 为遍历数组当前的索引值
• List<List<Integer>> res 为返回的结果集

回溯方法 backtrack 的方法签名：

private void backtrack(int[] nums,int cur,List<List<Integer>> res)

算法流程：

• 当 cur == nums.length 时，说明递归结束，直接 return。
• 当cur == 0 时，我们直接初始化一个 list ,将 cur[0] 添加到这个 list 中，并将 list 添加到结果集 res 中。
• 否则，我们将结果集的每一个 list 依次取出，将 cur[i] 组合到 list 的各个位置，构成一个新的 list 并添加到结果集 res 中

流程示意图：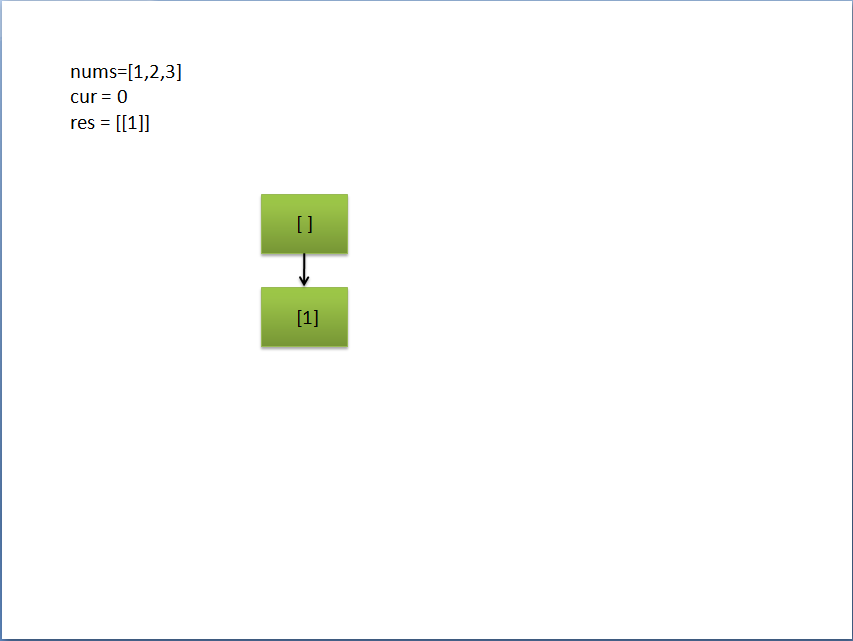

代码

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        backtrack(nums,0,res);
        return res;
    }
    private void backtrack(int[] nums,int cur,List<List<Integer>> res){
        if(cur == nums.length)
            return;
        if(cur == 0){
            List<Integer> list = new ArrayList<>();
            list.add(nums[cur]);
            res.add(list);
        }else {
            int size = res.size();
            for(int i = 0; i < size; i++){
                List<Integer> list = res.remove(0);
                for(int j = 0; j <= list.size(); j++){
                    List<Integer> tmp = new ArrayList<>(list);
                    tmp.add(j,nums[cur]);
                    res.add(tmp);
                }
            }
        }
        backtrack(nums,cur + 1,res);
    }
}

复杂度分析

• 时间复杂度

可以通过上面的流程示意图进行分析得到，我们算法的时间复杂度为，其中 N 为 nums 数组的长度。

• 空间复杂度

因为，我们的算法涉及到递归，递归深度为 nums 数组的长度，所以额外空间复杂度为：