数学函数

三角函数

sin()/cos()/tan()三角函数

  1. import numpy as np 
  3. arr = np.array([0, 30, 60, 90, 120, 150, 180]) 
  4. #计算arr数组中给定角度的三角函数值
  5. #通过乘以np.pi/180将其转换为弧度
  6. print(np.sin(arr * np.pi/180)) 
  7. print(np.cos(arr * np.pi/180)) 
  8. print(np.tan(arr * np.pi/180))

arcsin()/arccos()/arctan()/degrees()反三角函数

  1. import numpy as np 
  3. arr = np.array([0, 30, 60, 90]) 
  4. #正弦值数组
  5. sinval = np.sin(arr*np.pi/180) 
  6. print(sinval) 
  7. #计算角度反正弦，返回值以弧度为单位
  8. cosec = np.arcsin(sinval) 
  9. print(cosec) 
  10. #通过degrees函数转化为角度进行验证
  11. print(np.degrees(cosec)) 
  12. #余弦值数组
  13. cosval = np.cos(arr*np.pi/180) 
  14. print(cosval) 
  15. #计算反余弦值，以弧度为单位
  16. sec = np.arccos(cosval) 
  17. print(sec) 
  18. #通过degrees函数转化为角度进行验证
  19. print(np.degrees(sec)) 
  20. #下面是tan()正切函数 
  21. tanval = np.tan(arr*np.pi/180) 
  22. print(tanval) 
  23. cot = np.arctan(tanval) 
  24. print(cot) 
  25. print(np.degrees(cot))

舍入函数

around()

该函数返回一个十进制数，并将数值四舍五入到指定的小数位上。

  1. numpy.around(a,decimals)
  3. 其中：
  4. * a：要输入的数组
  5. * decimals：要舍入的小数位数。默认为0，如果为负数，则小数点移到整数左侧。
  1. import numpy as np 
  3. arr = np.array([12.202, 90.23120, 123.020, 23.202]) 
  4. print(arr) 
  5. print("数组值四舍五入到小数点后两位",np.around(arr, 2)) 
  6. print("数组值四舍五入到小数点后-1位",np.around(arr, -1))  
  8. # 输出内容如下：
  9. """
  10. [12.202 90.2312 123.02 23.202]
  11. 数组值四舍五入到小数点后两位[12.2 90.23 123.02 23.2]
  12. 数组值四舍五入到小数点后-1位[10. 90. 120. 20.]
  13. """

floor()

该函数表示对数组中的每个元素向下取整数，即返回不大于数组中对应元素值的最大整数。

  1. import numpy as np
  3. a = np.array([-1.8,  1.1,  -0.4,  0.9,  18])
  4. #对数组a向下取整
  5. print (np.floor(a))
  7. # 输出结果如下：
  8. """
  9. [-2.  1. -1.  0. 18.]
  10. """

ceil()

该函数与**floor()**函数相反，表示向上取整。

  1. import numpy as np
  3. a = np.array([-1.8,  1.1,  -0.4,  0.9,  18])
  4. #对数组a向上取整
  5. print (np.ceil(a))
  7. # 输出结果如下：
  8. """
  9. [-1.  2. -0.  1. 18.]
  10. """

算术运算

做算术运算时，输入数组必须具有相同的形状，或者符合数组的广播规则，才可以执行运算。

基础运算

add/subtract/multiple/divide加减乘除

  1. import numpy as np
  3. a = np.arange(9, dtype = np.float_).reshape(3,3)
  4. #数组a
  5. print(a)
  6. #数组b
  7. b = np.array([10,10,10])
  8. print(b)
  10. #数组加法运算
  11. print(np.add(a,b))
  13. #数组减法运算
  14. print(np.subtract(a,b))
  16. #数组乘法运算
  17. print(np.multiply(a,b))
  19. #数组除法运算
  20. print(np.divide(a,b))
  22. # 输出结果如下：
  23. """
  24. [[0. 1. 2.]
  25.  [3. 4. 5.]
  26.  [6. 7. 8.]]
  28. [10 10 10]
  30. [[10. 11. 12.]
  31.  [13. 14. 15.]
  32.  [16. 17. 18.]]
  34. [[-10.  -9.  -8.]
  35.  [ -7.  -6.  -5.]
  36.  [ -4.  -3.  -2.]]
  38. [[ 0. 10. 20.]
  39.  [30. 40. 50.]
  40.  [60. 70. 80.]]
  42. [[0.  0.1 0.2]
  43.  [0.3 0.4 0.5]
  44.  [0.6 0.7 0.8]]
  45. """

其他重要的算术运算

reciprocal()倒数

该函数对数组中的每个元素取倒数，并以数组的形式将它们返回。

  • 当数组元素的数据类型为整型（int）时，对于绝对值小于**1**的元素，返回值是**0**；
  • 当数组中包含**0**元素时，返回值将出现**overflow**（**inf**）溢出提示。 ```python import numpy as np

注意此处有0

a = np.array([0.25, 1.33, 1, 0, 100])

数组a默认为浮点类型数据

print(a)

对数组a使用求倒数操作

print (np.reciprocal(a))

b数组的数据类型为整形int

b = np.array([100], dtype = int) print(b)

对数组b使用求倒数操作

print( np.reciprocal(b) )

  1. <a name="oVXeY"></a>
  2. ### `power()`幂
  3. 该函数将`**a**`**数组中元素作为底数**，把`**b**`**数组中与**`**a**`**相对应的元素作幂**，最后**以数组形式返回两者的计算结果**。
  4. ```python
  5. import numpy as np
  7. a = np.array([10,100,1000]) 
  8. #a数组
  9. print ('我们的数组是；')
  10. #调用 power 函数
  11. print (np.power(a,2))    # [100 10000 1000000]
  13. #b数组
  14. b = np.array([1,2,3]) 
  15. print (b)
  16. 调用 power 函数
  17. print (np.power(a,b))

mod()取余

该函数返回两个数组相对应位置上的元素相除后的余数，与**remainder()**函数的作用相同。

import numpy as np

a = np.array([11,22,33])
b = np.array([3,5,7])

#a与b相应位置的元素做除法
print( np.mod(a,b))        # [2 2 5]等价于a%b
#remainder方法一样
print(np.remainder(a,b))     # [2 2 5]

复数数组处理函数

real()实部

返回复数数组的实部。

imag()虚部

返回复数数组的虚部。

conj()更改虚部的符号

通过更改虚部的符号，返回共轭复数。

angle()角度

返回复数参数的角度。

  • deg参数为True，返回的值以角度制表示；
  • deg参数为False，返回的值以弧度表示。

    示例

    ```python import numpy as np

a = np.array([-5.6j, 0.2j, 11., 1 + 1j]) print(a)

real()

print(np.real(a))

imag()

print(np.imag(a))

conj()

print(np.conj(a))

angle()

print(np.angle(a))

angle() 带参数deg

print(np.angle(a, deg=True))

输出结果如下：

“”” [-0.-5.6j 0.+0.2j 11.+0.j 1.+1.j ] [-0. 0. 11. 1.] [-5.6 0.2 0. 1. ] [-0.+5.6j 0.-0.2j 11.-0.j 1.-1.j ] [-1.57079633 1.57079633 0. 0.78539816] [-90. 90. 0. 45.] “””

<a name="b9YmB"></a>
# 统计函数
<a name="j3KaY"></a>
## `amin()`和`amax()`（计算最值）
对于二维数组来说，`axis=0`表示沿着垂直方向（**逐列**），`axis=1`表示沿着水平方向（**逐行**）。<br />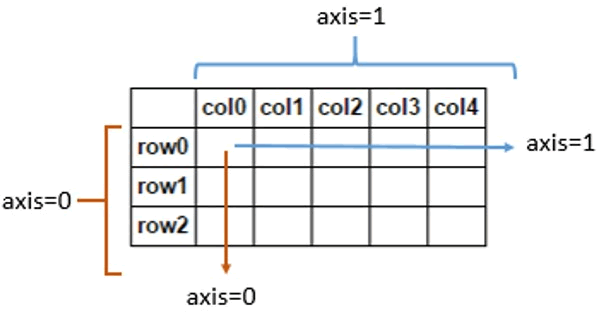![axis轴的方向](https://cdn.nlark.com/yuque/0/2022/gif/566095/1643248652045-3173e409-cc0b-4e14-98db-fa606e530c7c.gif#clientId=ub093ed0b-cf9c-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=z9Sdn&margin=%5Bobject%20Object%5D&originHeight=312&originWidth=600&originalType=url&ratio=1&rotation=0&showTitle=true&status=done&style=none&taskId=ud4ca7ece-301a-425c-b58e-a18be6860f5&title=axis%E8%BD%B4%E7%9A%84%E6%96%B9%E5%90%91 "axis轴的方向")
<a name="ML1hv"></a>
### `amin()`
沿指定的轴，**查找数组中元素的最小值**，并**以数组形式返回**。
<a name="VLshj"></a>
### `amax()`
沿指定的轴，**查找数组中元素的最大值**，并**以数组形式返回**。
```python
import numpy as np

a = np.array([[3, 7, 5], [8, 4, 3], [2, 4, 9]])
print('数组a是：')
print(a)
# amin()函数
print(np.amin(a))  # 不指定axis参数，默认查询整个数组
# 调用 amin() 函数，axis=1
print(np.amin(a, axis=1))  # 指定axis参数，按指定轴查询
# 调用amax()函数
print(np.amax(a))
# 再次调用amax()函数
print(np.amax(a, axis=0))

# 输出结果如下：
"""
数组a是：
[[3 7 5]
 [8 4 3]
 [2 4 9]]
2
[3 3 2]
9
[8 7 9]
"""

ptp()计算最值间的差值

即计算“最大值-最小值”。

import numpy as np

a = np.array([[2, 10, 20], [80, 43, 31], [22, 43, 10]])
print("原数组", a)
print("沿着axis 1:", np.ptp(a, 1))
print("沿着axis 0:", np.ptp(a, 0))

# 输出结果如下：
"""
原数组 [[ 2 10 20]
 [80 43 31]
 [22 43 10]]
沿着axis 1: [18 49 33]
沿着axis 0: [78 33 21]
"""

percentile()计算百分位数

该函数表示沿指定轴，计算数组中任意百分比分位数。
计算步骤如下：

  • percentile()会自动将数据从小到大排序，然后进行百分位数计算；
  • Numpy数学运算 - 图1；
  • index中的i表示整数部分，g表示小数部分；
  • Numpy数学运算 - 图2。 ```python numpy.percentile(a, q, axis)

其中：

  • a：输入数组
  • q：要计算的分位数，在0~100之间
  • axis：指定的轴计算百分比分位数 python import numpy as np

a = np.array([[2, 10, 20], [80, 43, 31], [22, 43, 10]]) print(“数组a:”, a) print(“沿着axis=0计算百分位数”, np.percentile(a, 10, 0)) print(“沿着axis=1计算百分位数”, np.percentile(a, 10, 1))

输出结果如下：

“”” 数组a: [[ 2 10 20] [80 43 31] [22 43 10]] 沿着axis=0计算百分位数 [ 6. 16.6 12. ] 沿着axis=1计算百分位数 [ 3.6 33.4 12.4] “””

<a name="sSSDT"></a>
## `median()`计算中位数
```python
import numpy as np

a = np.array([[30, 65, 70], [80, 95, 10], [50, 90, 60]])
# 数组a:
print(a)
# median()
print
np.median(a)
# axis 0
print
np.median(a, axis=0)
# axis 1:
print(np.median(a, axis=1))

# 输出结果如下：
"""
[[30 65 70]
 [80 95 10]
 [50 90 60]]
[65. 80. 60.]
"""

mean()计算算术平均值

该函数表示沿指定的轴，计算数组中元素的算术平均值（即元素的总和/元素的数量）。

import numpy as np

a = np.array([[1, 2, 3], [3, 4, 5], [4, 5, 6]])
print('我们的数组是：')
print(a)
print('调用 mean() 函数：')
print(np.mean(a))
print('沿轴 0 调用 mean() 函数：')
print(np.mean(a, axis=0))
print('沿轴 1 调用 mean() 函数：')
print(np.mean(a, axis=1))

# 输出结果如下：
"""
[[1 2 3]
 [3 4 5]
 [4 5 6]]
调用 mean() 函数：
3.6666666666666665
沿轴 0 调用 mean() 函数：
[2.66666667 3.66666667 4.66666667]
沿轴 1 调用 mean() 函数：
[2. 4. 5.]
"""

average()计算加权平均值

加权平均值是将数组中各数值x相应的权数，再对权重值求总和，最后将权重总和/总的单位数（即因子个数）。

  • average()函数可接受一个axis参数，如不指定，则将数组展开为一维数组；
  • 若不指定权重，相当于求算术平均值。

    示例

    现有数组[1, 2, 3, 4]和相应权重数组[4, 3, 2, 1]，加权平均值计算如下：
    加权平均值=（1 * 4 + 2 * 3 + 3 * 2 + 4 * 1）/（4 + 3 + 2 + 1）
    ```python

    不指定axis参数——默认展开为一维数组

    import numpy as np

a = np.array([1, 2, 3, 4]) print(‘a数组是：’) print(a)

average()函数：

print(np.average(a)) # 若不指定权重相当于对数组求均值 we = np.array([4, 3, 2, 1]) # 设置权重 print(np.average(a, weights=we)) # 计算加权平均值

returned 为Ture，则返回加权平均数以及权重的和

print(np.average([1, 2, 3, 4], weights=[4, 3, 2, 1], returned=True))

输出结果如下：

“”” a数组是： [1 2 3 4] 2.5 2.0 (2.0, 10.0) “””

指定axis参数

import numpy as np

a = np.arange(6).reshape(3, 2)

多维数组a

print(a)

修改后数组

wt = np.array([3, 5]) print(np.average(a, axis=1, weights=wt))

修改后数组

print(np.average(a, axis=1, weights=wt, returned=True))

输出结果如下：

“”” [[0 1] [2 3] [4 5]] [0.625 2.625 4.625] (array([0.625, 2.625, 4.625]), array([8., 8., 8.])) “””

<a name="M9T4e"></a>
## `var()`方差
方差，也叫样本方差。<br />先计算全体样本的平均值`M`，再求每个样本值与均值之差的平方和，最后对差的平方和求均值。公式如下：<br />![](https://cdn.nlark.com/yuque/__latex/99ad0d9c876dd1c9f3669e96c934074a.svg#card=math&code=s%5E2%3D%5Cfrac%7B%28x_1-M%29%5E2%2B%28x_2-M%29%5E2%2B%28x_3-M%29%5E2%2B%C2%B7%C2%B7%C2%B7%2B%28x_n-M%29%5E2%7D%7Bn%7D&id=W1gyO)
```python
import numpy as np

print(np.var([1, 2, 3, 4]))

# 输出结果如下：
"""
1.25
"""

std()标准差

标准差是方差的算术平均根，用来描述一组数据平均值的分散程度。

  • 一组数据的标准差较大，说明大部分数值和其平均值之间差异较大；
  • 若标准差较小，表示这组数值比较接近平均值。

Numpy数学运算 - 图3

import numpy as np

print(np.std([1, 2, 3, 4]))

# 输出结果如下：
"""
1.118033988749895
"""