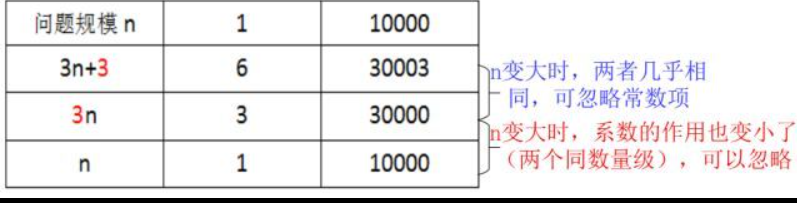
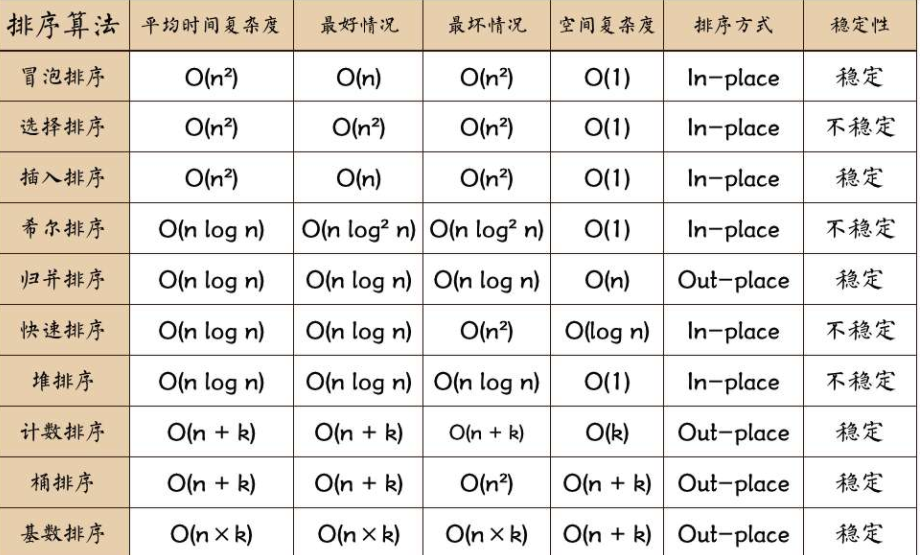
时间复杂度

比如：
T(n)=n+1 忽略常数项 T(n)~n
T(n)=n+n^2 忽略低阶项 T(n)~n^2
T(n)=3n 忽略最高阶的系数 T(n)~n

1.数字冒泡排序


public class BubbleSort {
  public static void main(String[] args) {
    int[] arr = {1, 3, 4, 6, 8, 29, 0, 78, 78, 11};
    System.out.println("冒泡排序前的结果" + Arrays.toString(arr));
    bubbleSort(arr);
  }
  private static void bubbleSort(int[] arr) {
    if (arr == null || arr.length < 2) {
      return;
    }
    for (int i = 0; i < arr.length - 1; i++) {
      boolean flag = true;
      for (int j = 0; j < arr.length - 1 - i; j++) {
        if (arr[j] > arr[j + 1]) {
          flag = false;
          int temp;
          temp = arr[j];
          arr[j] = arr[j + 1];
          arr[j + 1] = temp;
        }
      }
      // 一趟下来是否发生位置交换
      if (flag) {
        break;
      }
    }
    System.out.println("冒泡排序后的结果" + Arrays.toString(arr));
  }
}
结果
冒泡排序前的结果[1, 3, 4, 6, 8, 29, 0, 78, 78, 11]
冒泡排序后的结果[0, 1, 3, 4, 6, 8, 11, 29, 78, 78]

String字符串排序

自己写工具类

public static void main(String[] args) {
    String[] arr = {"nba", "abc", "cha", "cba", "zz", "qq", "haha"};
    printArray(arr);
    System.out.println("---------------------------------");
    sortString(arr);
    printArray(arr);
  }
  private static void sortString(String[] arr) {
    for (int i = 0; i < arr.length; i++) {
      for (int j = i + 1; j < arr.length; j++) {
        // 字符串比较用compareTo方法
        if (arr[i].compareTo(arr[j]) > 0) {
          swap(arr, i, j);
        }
      }
    }
  }
  private static void swap(String[] arr, int i, int j) {
    String temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
  }
  private static void printArray(String[] arr) {
    System.out.print("[");
    for (int i = 0; i < arr.length; i++) {
      if (i != arr.length - 1) {
        System.out.print(arr[i] + ", ");
      } else {
        System.out.println(arr[i] + "]");
      }
    }
  }
}
结果如下
[nba, abc, cha, cba, zz, qq, haha]
---------------------------------
[abc, cba, cha, haha, nba, qq, zz]

    public static String toString(Object[] a) {
        if (a == null)
            return "null";
        int iMax = a.length - 1;
        if (iMax == -1)
            return "[]";
        StringBuilder b = new StringBuilder();
        b.append('[');
        for (int i = 0; ; i++) {
            b.append(String.valueOf(a[i]));
            if (i == iMax)
                return b.append(']').toString();
            b.append(", ");
        }
    }

调用Arrays.toString方法

public static String toString(int[] a) {
        if (a == null)
            return "null";
        int iMax = a.length - 1;
        if (iMax == -1)
            return "[]";
        StringBuilder b = new StringBuilder();
        b.append('[');
        for (int i = 0; ; i++) {
            b.append(a[i]);
            if (i == iMax)
                return b.append(']').toString();
            b.append(", ");
        }
    }

2.选择排序

场景
从众多苹果中挑了一个最大的装入袋子，然后又从剩下的苹果中挑出了最大的放入口袋

其实就是选择排序的思想，选择排序就是不断地从未排序的元素中选择最大（或最小）的元素放入已排好序的元素集合中，直到未排序中仅剩一个元素为止

我先从这些元素中选出一个最小的（或最大的），和第一个元素进行交换，这样第一个元素就是最小的，第一个元素位置就变成有序区间了

那如何选出最小的一个元素呢？
很容易想到：先随便选一个元素假设它为最小的元素（默认为无序区间第一个元素），然后让这个元素与无序区间中的每一个元素进行比较，如果遇到比自己小的元素，那更新最小值下标，直到把无序区间遍历完，那最后的最小值就是这个无序区间的最小值

代码demo


public class SelectionSortDemo {
  public static void main(String[] args) {
    int[] arr = {1, 11, 1, 2, 3, 2, 3, 4, 6, 8, 2, 11};
    System.out.println("选择排序前的结果" + Arrays.toString(arr));
    selectionSort(arr);
  }
  private static void selectionSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
      for (int j = arr.length - 1; j > i; j--) {
        if (arr[i] > arr[j]) {
          int temp;
          temp = arr[j];
          arr[j] = arr[i];
          arr[i] = temp;
        }
      }
    }
    System.out.println("选择排序后的结果" + Arrays.toString(arr));
  }
}

demo2


  private static void selectionSort1(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
      int minIndex = i;
      for (int j = i + 1; j < arr.length; j++) {
        if (arr[j] < arr[minIndex]) {
          minIndex = j;
        }
      }
    int temp = arr[minIndex];
    arr[minIndex] = arr[i];
    arr[i] = temp;    }
    System.out.println("选择排序后的结果" + Arrays.toString(arr));
  }

3.插入排序

场景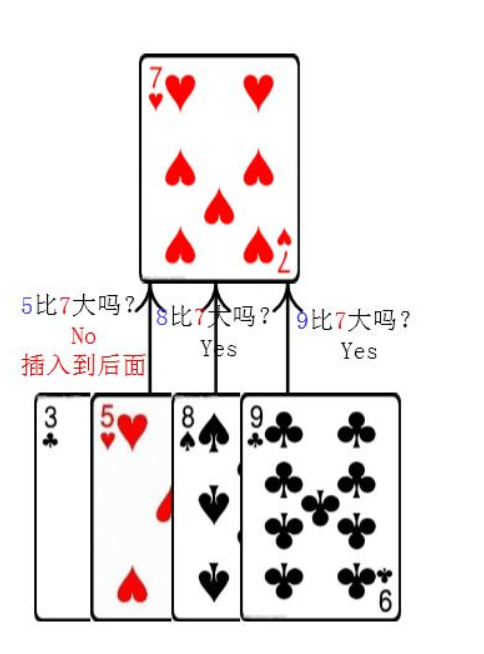

所谓直接插入排序，就是把未排序的元素一个一个地插入到有序的集合中插入，把有序集合从后向前扫一遍，找到合适的位置插入

  public static void main(String[] args) {
    int[] arr = {1, 3, 4, 6, 8, 2, 100};
    System.out.println("插入排序前的数组为" + Arrays.toString(arr));
    insertionSort(arr);
  }
  public static void insertionSort(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
      // 将arr[i] 查放入到正确的位置
      inserToRightPosition(arr, i);
    }
    System.out.println("插入排序后的数组为" + Arrays.toString(arr));
  }
  private static void inserToRightPosition(int[] arr, int i) {
    // 备份待插元素
    int inserted = arr[i];
    int j = i - 1;
    for (; j >= 0 && arr[j] > inserted; j--) {
      arr[j + 1] = arr[j];
    }
    // 将待插元素插入正确的位置
    arr[j + 1] = inserted;
  }
执行结果
插入排序前的数组为[1, 3, 4, 6, 8, 2, 100]
插入排序后的数组为[1, 2, 3, 4, 6, 8, 100]

Java 学习

常见排序算法