The signs of Overfitting

Accuracy on the test data

At first, the accuracy is improving, then the learning gradually slows down. Finally, the accuracy pretty much stops improving. Later epochs merely see small stochastic fluctuations near the value of the accuracy at epoch which accuracy stops improving.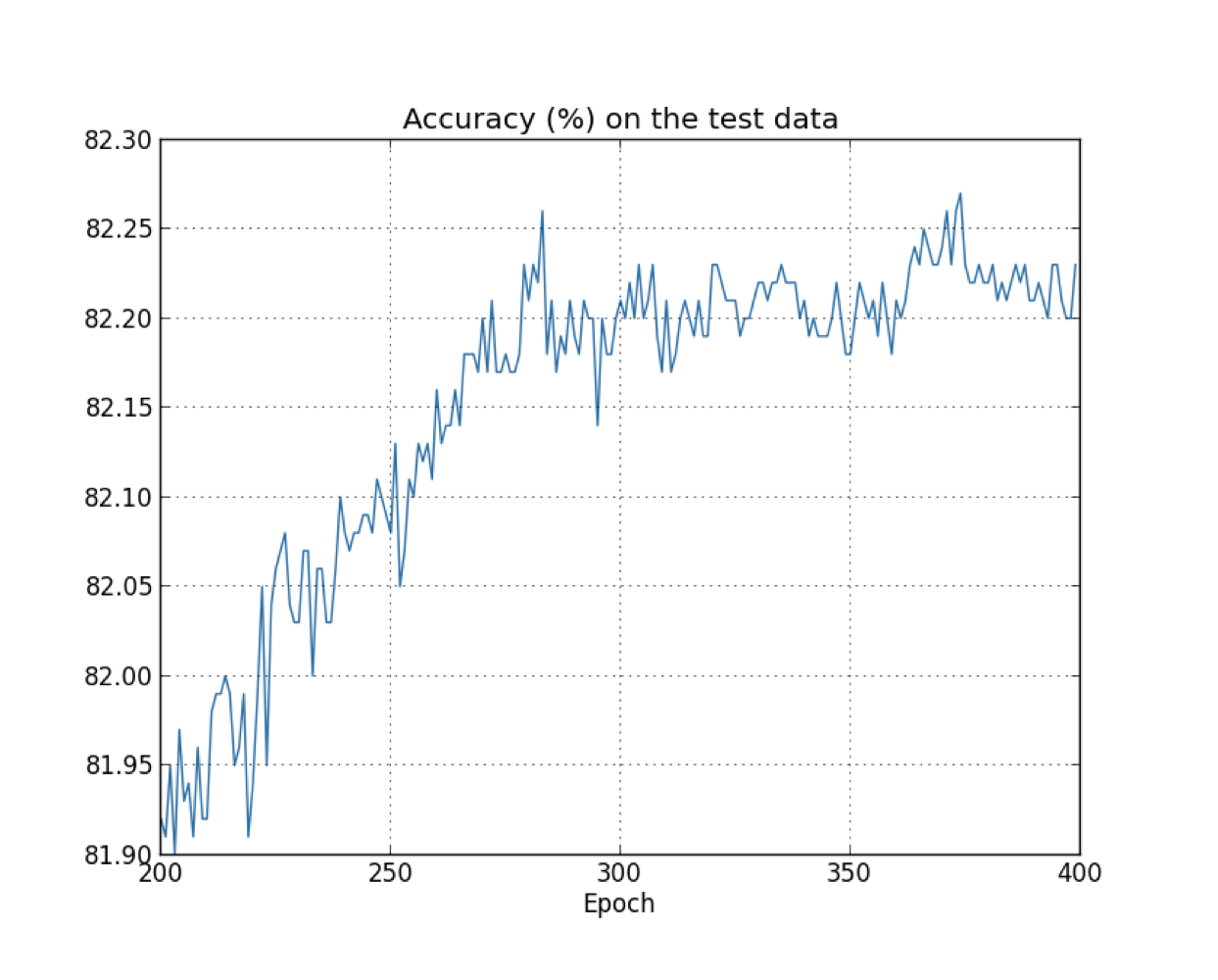

Cost on the test data

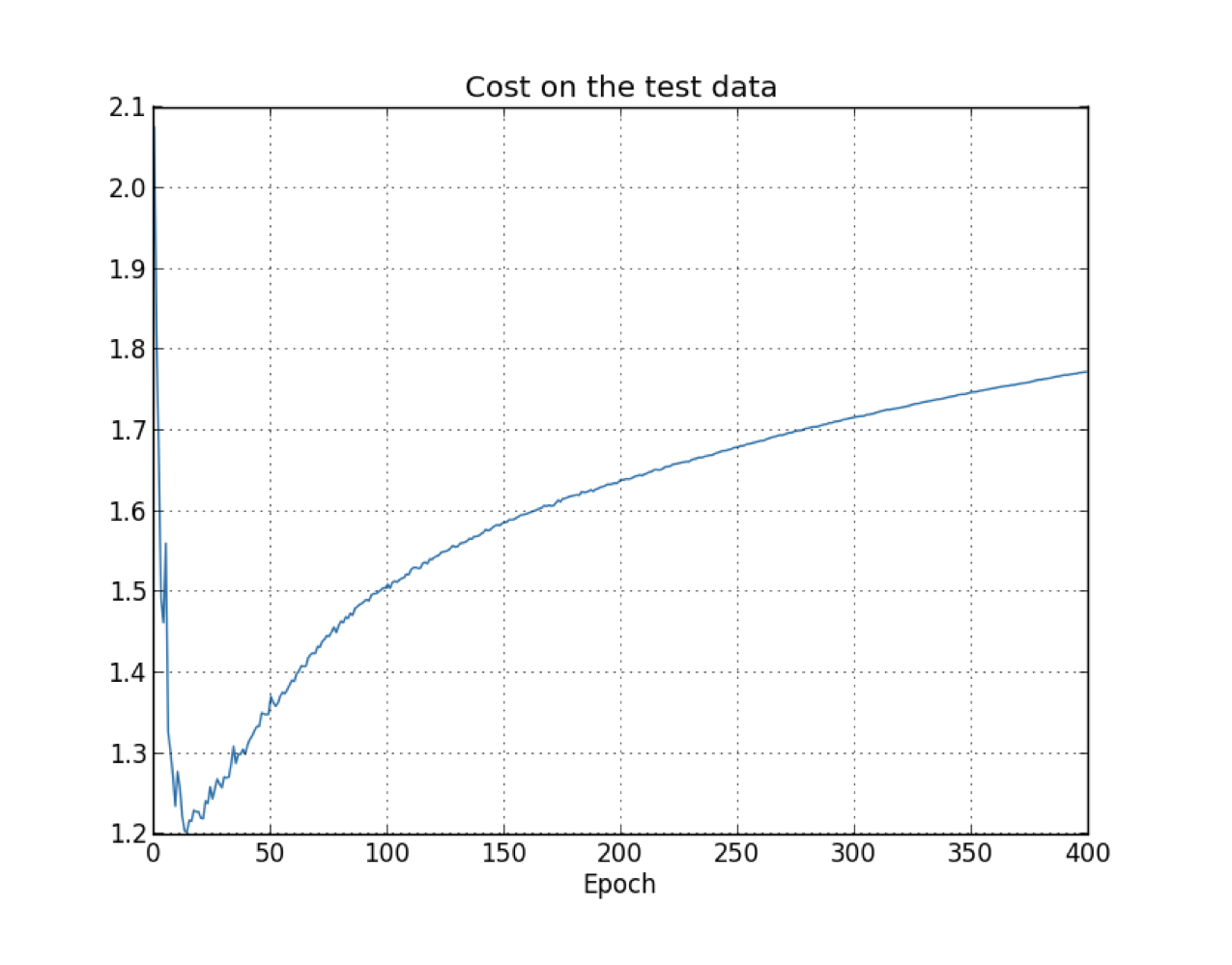
The cost on the test data is improving until epochs 15, then, the cost get worse.

Accuracy on the training data

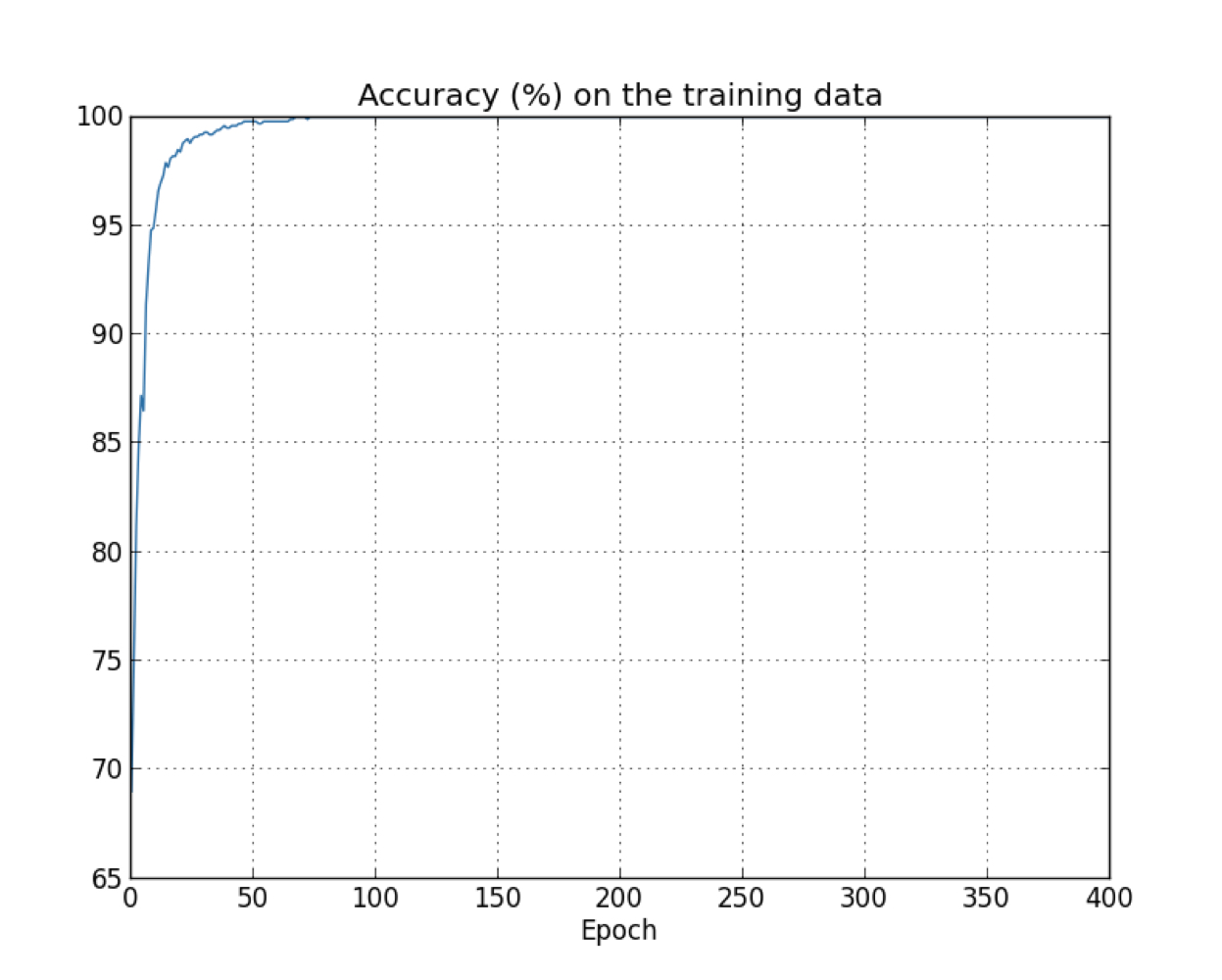
accuracy on the training data is 100%, while the the the test accuracy tops out at just 82.27%. So the network is learning about the peculiarities of the training set (memorizing the training set, without understanding digits well enough to generalize to the test set).

Q1: In sign 1, the sign of overfitting shown at epoch 280, while in sign 2, the sign of overfitting shown at epoch 15. Which is whether we should regard epoch 15 or 280 as the pint at which overfitting is coming to dominate learning?

What we really care about is to improve the accuracy of test data, while the cost on the test data is no more than a proxy for classification accuracy, so it’s make more sense to regard epoch 280 as the point beyond which overfitting is dominating learning in our neuroal network. (sign1 is accuracy, sign2 is cost)

Detect overfitting

Keeping track of accuracy on the test data

If the accuracy on the test data is no longer improve, stop training.

Use validation data set(Early stopping)

Split the dataset into three set, training set, validation set and test set.

• Training set: trian the model
• Test set: final test the accuracy of the model when the model is trained.
• Validation set: compute the classificaiton accuracy at the end of each epoch. Once the classificaiton accuracy on the validation set has saturated, stop training. (continue training until we’re confident that the accuracy has saturated (train for another n epochs)).
• why validation set?
  • The role of validation set is to find a good set of hyper-parameters, if we use test set, we may end up with finding a set of hyper-parameter that peculiarities of the test set, but where the performance of the network won’t generalize to othe data sets.
  • We guard against that by figuring out the hyper-parameters using the validation set; then do a final evaluation of accuracy using the test set, that gives us confidentce that our results on the test set are a true measure of how well our neural network generalizes.

    Deal with overfitting

    One best way to reduce overfitting

    Increase the size of training data. With enough training data, it’s difficult foreven a very large network to overfit.

    Regularization

    L2 regularization

    Intro

    The regularization techniques is about to add an extra term to the cost function, firstly, let’s check the most commonly used regularization technique, which called weight decay or L2 regularization.
    Below is the regulaeized cross-entropy:
    
    the second term is the sum of the squares of all the weights in the network, and scaled by a factor , n is the size of the training set, and is a hyper-parameter.

, is the original cost function. when the value of , is small, we prefer to minimize the original cost function, when is large, we prefer small weights.

How to apply regularized cost function

In order to apply regulized cost function, we need to figure out how to apply SGD learning algorithm in a regularized neural network. In particular, we need to know how to compute the partial derivatives of cost function with respect to weights and bias.


result: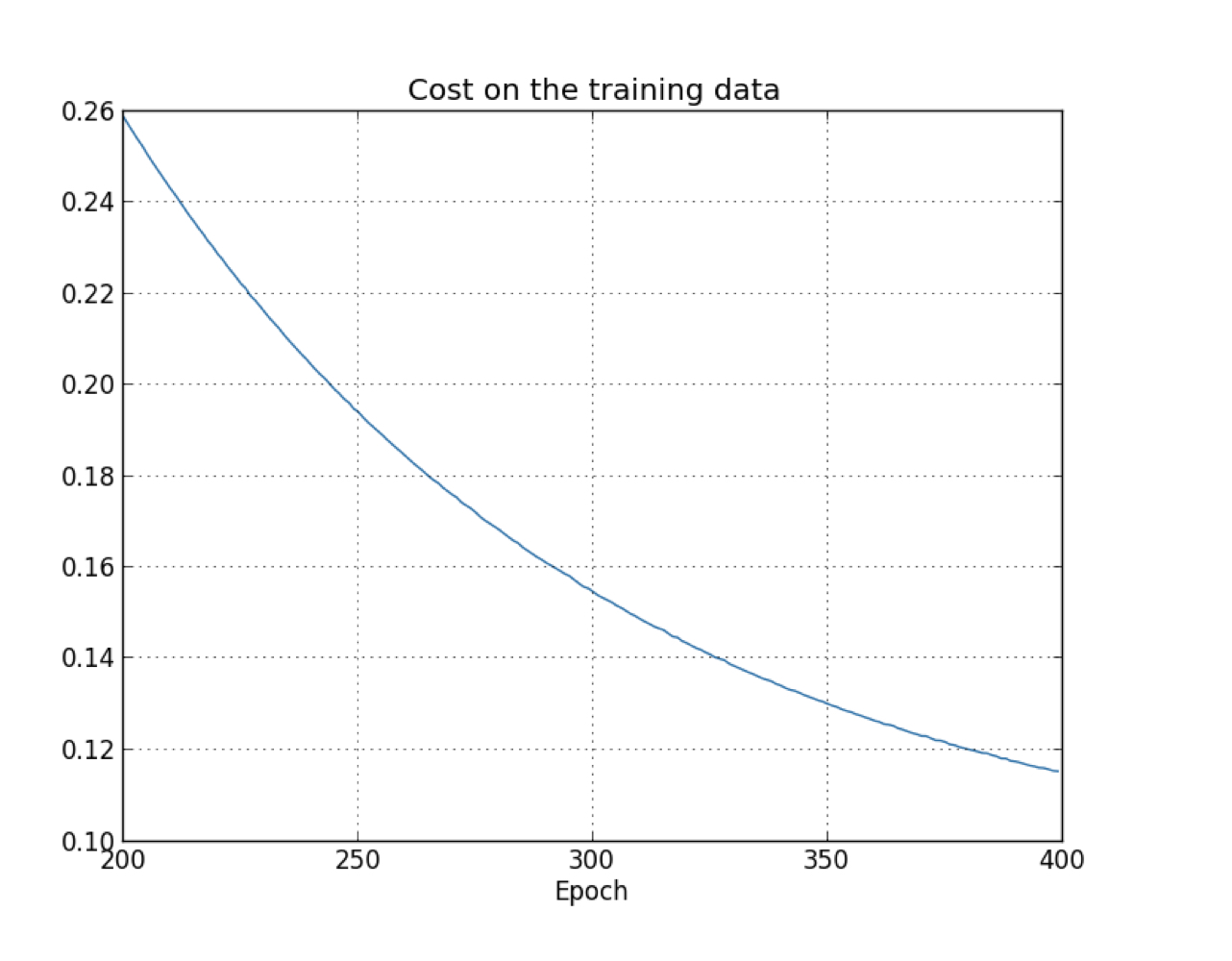


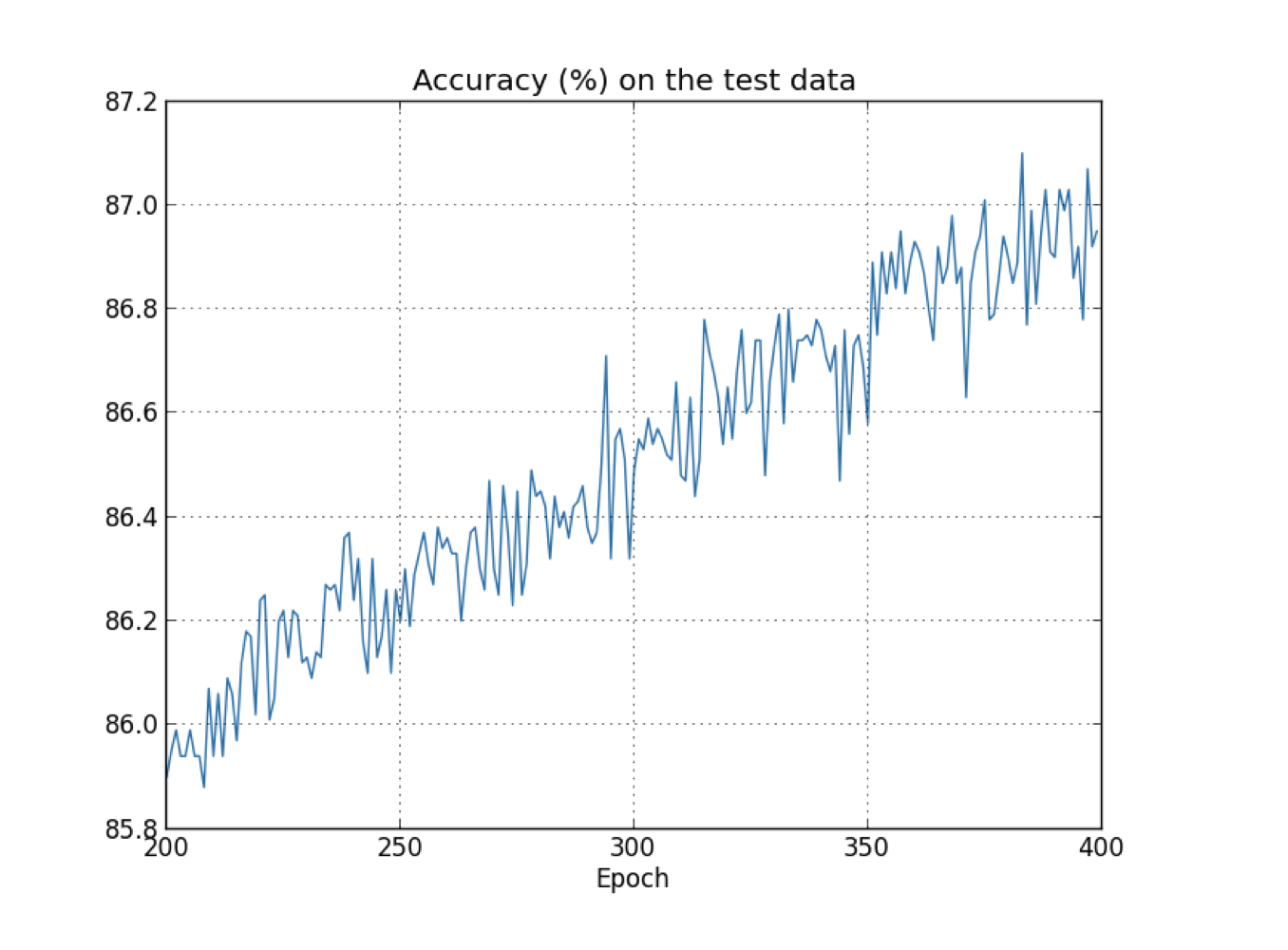
Compare to the previous one, this time, the accuracy keep imcreasing in all the 400 epochs, the effect of overfitting is obviously reduced.

L1 regularization

Formula

Derivative

, where sgn means the sign of w, if w is negativa, then it reduces, if positive, then plus.

Dropout

The procedue of dropout

First, the network temporarily and randomly delte half of the neurons in the hidden layers, then keep the input and output neurons unchanged. Then we forward-propagate the input through the modified network, then bp the result and properly update the resered weights and biases.
Then (next iteration), first restore the network, and then temporarily and randomly delte half of the newrons in the hidden layers again. Learn and bp same as above.
…
Finally, when we ran the full network that means that twice as many hidden neurons will be active. To compensate for that, we halve the weights outgoing from the hidden neurons.

Artificially expanding the training data

Data augmentation ss