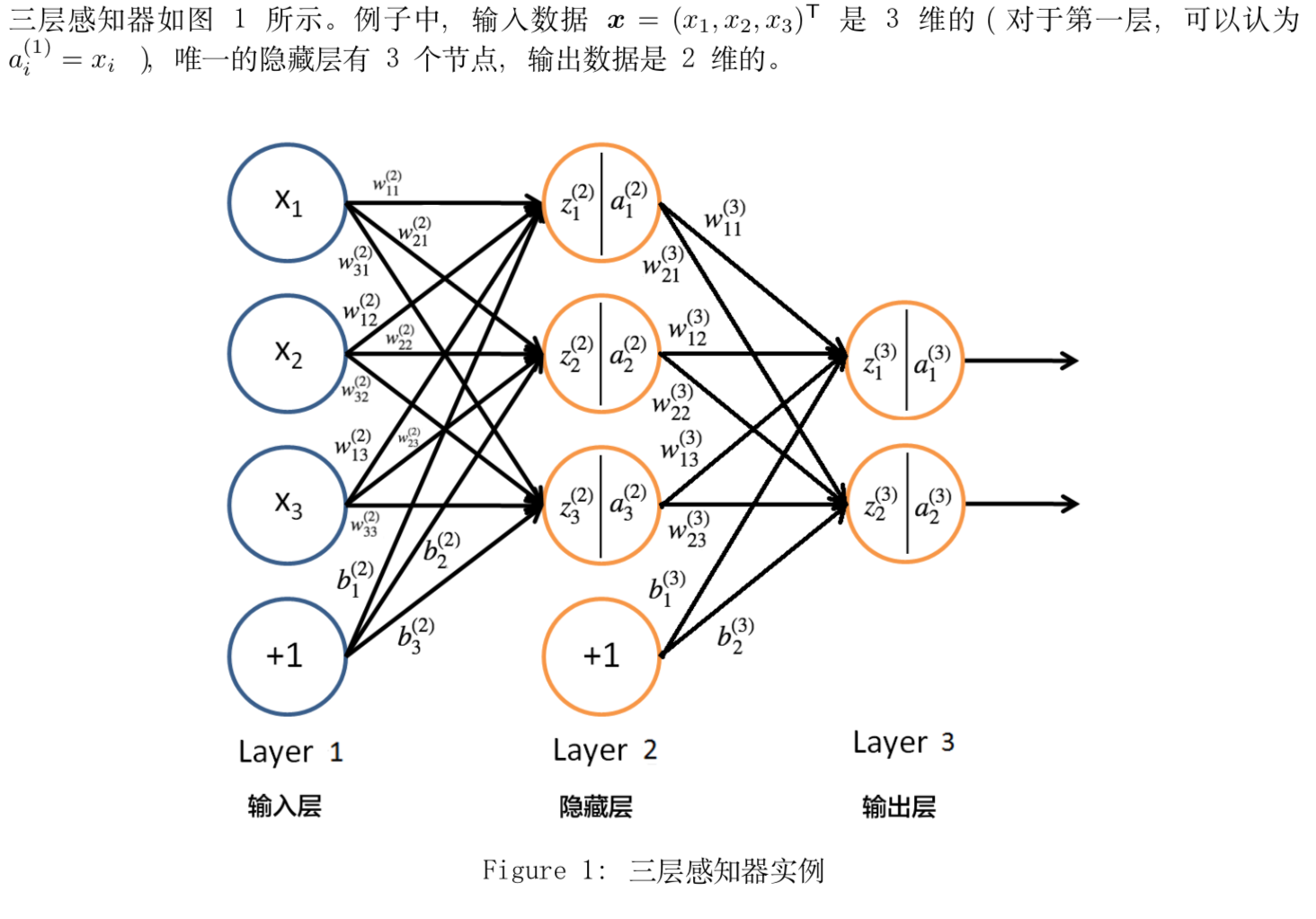
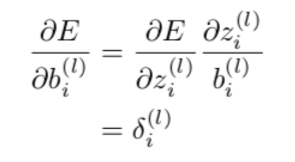反向传播的作用

梯度下降法中需要利用损失函数对所有参数的梯度来寻找局部最小值点；
而反向传播算法就是用于计算该梯度的具体方法，其本质是利用链式法则对每个参数求偏导。

反向传播的公式推导

反向传播算法原理；基本思想
（1）先计算每一层的状态和激活值，直到最后一层（即信号是前向传播的）；
（2）计算每一层的误差，误差的计算过程是从最后一层向前推进的（这就是反向传播算法名字的由来）；
（3）更新参数（目标是误差变小）。迭代前面两个步骤，直到满足停止准则（比如相邻两次迭代的误差的差别很小）。
反向传播BP算法 - 图1
反向传播BP算法 - 图2

误差反向传播

代价函数

仅和权重矩阵

和偏置向量

相关，调整权重和偏置可以减小或增大代价误差
所有训练数据的总体代价：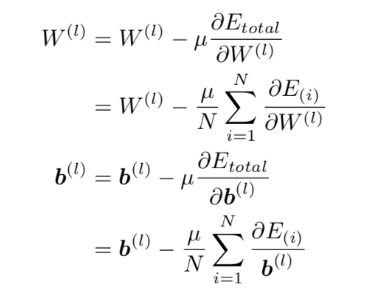
反向传播BP算法 - 图3
image.png

输出层的权重参数更新

image.png
image.png
image.png

隐藏层的权重参数更新

image.png
image.png
image.png

输出层和隐藏层的偏置参数更新

image.png

BP算法的四个核心公式

image.png
image.png

BP反向传播算法流程

image.png
image.png

反向传播解释梯度消失的原因

image.png

参考Blogs：
神经网络BP反向传播算法原理和详细推导流程

最后如果转载，麻烦留个本文的链接，因为如果读者或我自己发现文章有错误，我会在这里更正，留个本文的链接，防止我暂时的疏漏耽误了他人宝贵的时间。