作者：这波能反杀

队列是一种先进先出的数据结构。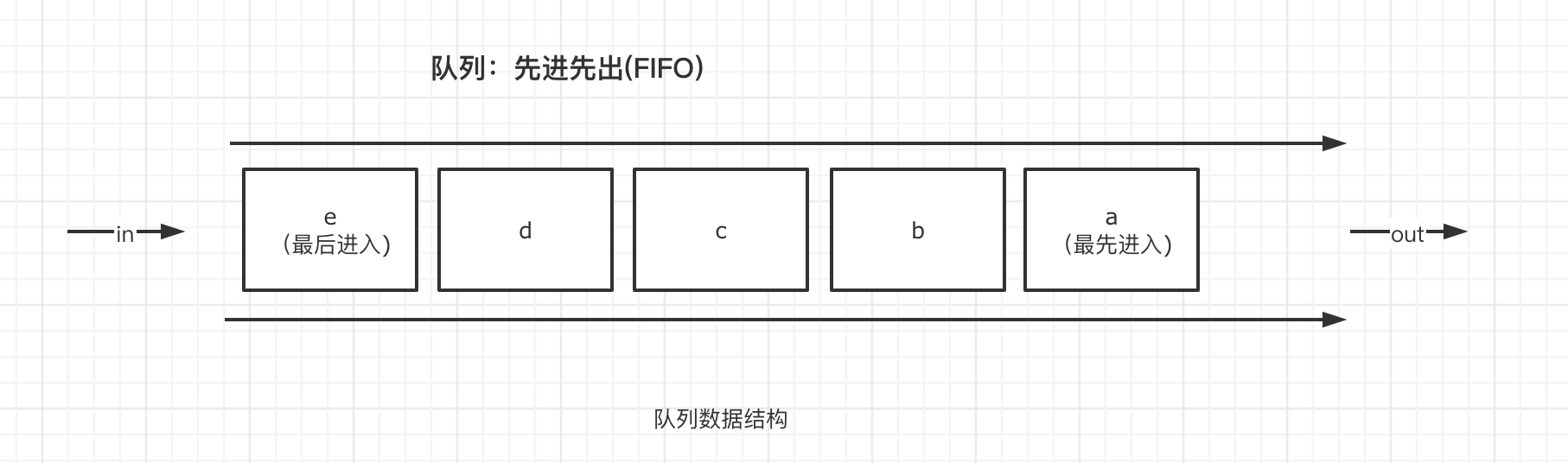

image.png

如果要将队列运用到实践中，很容易就能够想到会有如下操作

  1. 从队列最后入队
  2. 从队列头部出队
  3. 从队列任意位置离队「有其他事情」
  4. 从队列任意位置插队「特殊权利」
  5. 清空队列

如果要用代码来实现一个队列对象，应该怎么办？

在思考这个问题之前，我们需要讨论一下使用什么样的基础数据结构来保存队列的数据。如果你对数组很熟悉，那么就能够很自然的想到使用数组来存储队列数据，但是我们仔细分析一下会发现，上面这些方法，数组全都已经实现过了。因此我们常常在实践中可以直接使用数组来表达一个队列。不过这样的话，就失去了学习的意义。因此我们基于更基础的对象字面量来表达队列，使用从 0 开始的数字作为 key 值，构建一个类数组对象，如下

  1. this.queue = {
  2.   0: 'A',
  3.   1: 'B',
  4.   2: 'C',
  5.   3: 'D'
  6. }

序列表示队列位置，序列对应的值，表示队列成员。

那么，队列对象的基本代码结构就应该如下

  1. class Queue {
  2.   constructor() {
  3.     this.length = 0
  4.     this.queue = {}
  5.   }
  7.   // 从队列尾部进入
  8.   push(node) {}
  10.   // 从队列头部出队
  11.   shift() {}
  13.   // 特殊情况的插队处理，在 i 前面插队
  14.   inset(i, node) {}
  16.   // 特殊情况的离队处理，队列中的任意位置离队
  17.   out(i) {}
  19.   clear() {}
  20. }

接下来就是实现具体的功能函数。

push，从队列尾部进入队列，该方法实现比较简单，当有一个成员入队，那么队列的长度自然要加 1，并且新增序列，用于对应新加入的队列成员

  1. push(node) {
  2.   this.queue[this.length] = node
  3.   this.length++
  4.   return this.queue
  5. }

shift，从队列头部出队。假设我们已经有这样一个队列，如下

  1. this.queue = {
  2.   0: 'A',
  3.   1: 'B',
  4.   2: 'C',
  5.   3: 'D',
  6.   4: 'F'
  7. }

从队列首部删除一个，那么队列就变成

  1. this.queue = {
  2.   0: 'B',
  3.   1: 'C',
  4.   2: 'D',
  5.   3: 'F'
  6. }

很容易能发现，序列始终保持从 0 开始，这也是队列的基本规则。之前的首位出去之后，第二个元素成为了新的队首。最终序列 4 消失不见，而队列成员对应的序列则依次向前进了一位。明白这个变化之后，代码实现就变得容易了

  1. // 从队列头部出队
  2. shift() {
  3.   const rq = this.queue[0]
  4.   for (let i = 0; i < this.length - 1; i++) {
  5.     this.queue[i] = this.queue[i + 1]
  6.   }
  7.   delete this.queue[this.length - 1]
  8.   this.length--;
  9.   return rq
  10. }

insert 方法 与 out 方法同理，删除或者新增一个队列成员之后，我们针对性的调整序列与成员之间的对应关系即可。完整代码如下：

  1. class Queue {
  2.   constructor() {
  3.     this.length = 0
  4.     this.queue = {}
  5.   }
  7.   // 从队列尾部进入
  8.   push(node) {
  9.     this.queue[this.length] = node
  10.     this.length++
  11.     return this.queue
  12.   }
  14.   // 从队列头部出队
  15.   shift() {
  16.     const rq = this.queue[0]
  17.     for (let i = 0; i < this.length - 1; i++) {
  18.       this.queue[i] = this.queue[i + 1]
  19.     }
  20.     delete this.queue[this.length - 1]
  21.     this.length--;
  22.     return rq
  23.   }
  25.   // 特殊情况的插队处理，在 i 前面插队
  26.   inset(i, node) {
  27.     this.length++
  28.     for (let k = this.length - 1; k > i; k--) {
  29.       this.queue[k] = this.queue[k - 1]
  30.     }
  31.     this.queue[i] = node
  32.     return this.queue
  33.   }
  35.   // 特殊情况的离队处理，队列中的任意位置离队
  36.   out(i) {
  37.     const rq = this.queue[i]
  38.     for (let k = i; k < this.length - 1; k++) {
  39.       this.queue[k] = this.queue[k + 1]
  40.     }
  42.     delete this.queue[this.length - 1]
  43.     this.length--
  44.     return rq
  45.   }
  47.   clear() {
  48.     this.length = 0
  49.     this.queue = {}
  50.   }
  51. }

运用到实践中时，可能还会新增更多额外的处理方式，例如：

  • 判断某个成员，是否正在队列中
  • 由于紧急情况，成员需要在队列中处于挂起状态去处理别的事情，激活之后不需要重新排队，而是直接处于队列的原有位置「如果队列往前移动了，也跟着移动，始终不出队」
  • 按照优先级排队，始终让优先级最高的队列成员，处于队首。因此这种情况之下，任何队列成员的变动都需要重新排序，确保队首的成员优先级最高，我们上一章节学习过的二叉堆，就可以实现这种优先级队列

**

思考题

10 个员工处理 1000+ 个来访客户的业务。这 1000+ 个客户会在一天内的不同时间陆续来访。那么如何利用队列的思维，来保证来访者的公平性「先到先处理」，以及保证来访任务的相对合理分配？

除此之外，你还能在生活中，发现那些队列的运用场景？