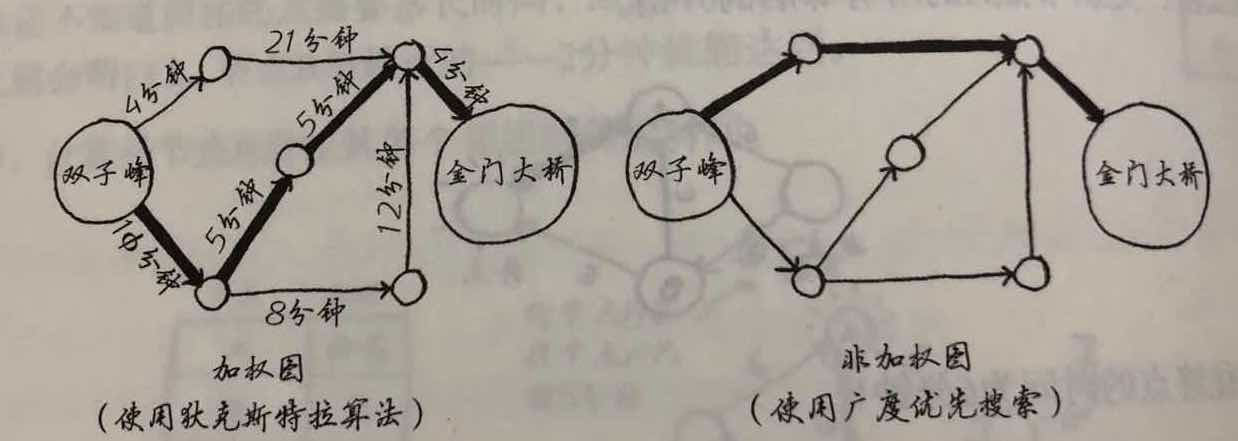
定义：
1.找出加权图中前往X的最短路经。
2.只适用于无向图。

image.png

步骤
1.找出最短时间可以到达的节点。
2.更新该点相邻点的开销。
3.重复这个过程。
4.计算最终路经。

术语

狄克斯特拉算法用于每条边都有关数字的图，这些数组称为权重。带权重的图称为加权图，不带权重为非加权图。不能使用于有向图中，有向图中可能存在环，导致死循环。

image.png

负权边

如果有负权边不能使用狄克斯特拉算法，例如以物换物的时候就会出现负权边。
狄克斯特拉算法基于一定会前往最低权重路径，这种假设仅在没有负权变边时成立。
在负权边的图中，要找出最短路径，可以使用另一种算法（贝尔曼-福德算法）。

实现

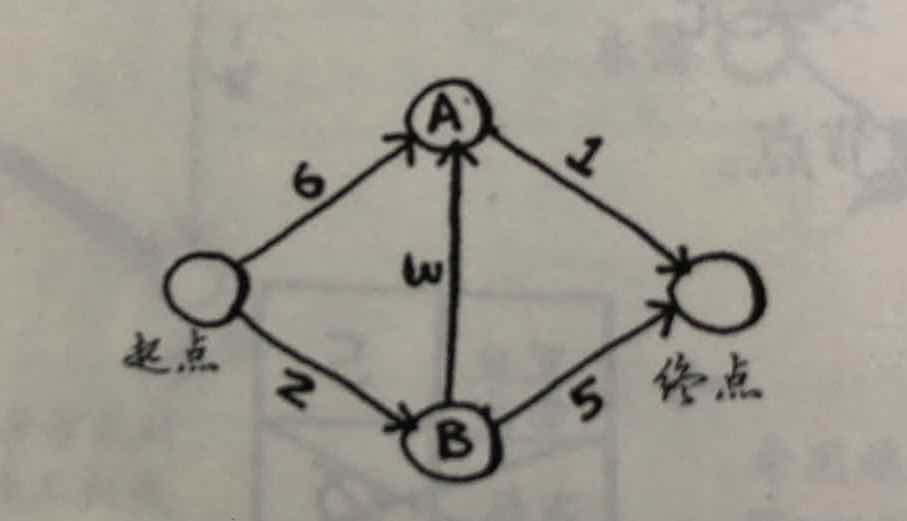
解决这个问题需要三个散列表
1.表示每一步的权重
2.存储开销权重
3.存储父节点

  1. let graph = {};
  3. //表示了每一步的权重
  4. //第一个散列表
  5. graph['start']={};
  6. graph['start']['a']=6;
  7. graph['start']['b']=6;
  8. //第二个散列表
  9. graph['a']={};
  10. graph['a']['fin']=1;
  11. graph['a']['b']=3;
  12. //第三个散列表
  13. graph['b']={};
  14. graph['b']['fin']=5;
  15. graph['b']['a']=3;
  18. //存储到达某节点需要权重
  19. let costst={};
  20. costst['a']=6;
  21. costst['b']=2;
  22. costst['fin']= Number.POSITIVE_INFINITY;//无穷大
  25. let parents={};
  26. parents['a']='start';
  27. parents['b']='start';
  28. parents['fin']= null;//未知
  31. /**
  32. 1.只要还有要处理的节点
  33. 2.获取离起点最近的节点
  34. 3.更新其邻近点的开销
  35. 4.如有邻近点开销被更新，同时更新其父节点
  36. */
  39.  //循环遍历花费找出最低权重元素并返回
  40. function find_lowest_cost_node(json_obj, arr) {
  41.   let lowest_cost = Infinity
  42.   let lowest_cost_node = null
  43.   for (let json_obj_node in json_obj) {
  44.     /**
  45.     判断当前key值对应的值是否小于当前最小开销
  46.     且不没有被处理过
  47.     */
  48.     if (json_obj[json_obj_node] < lowest_cost && arr.indexOf(json_obj_node) == -1) {
  49.       lowest_cost = json_obj[json_obj_node]
  50.       lowest_cost_node = json_obj_node
  51.     }
  52.   }
  53.   return lowest_cost_node
  54. }
  55. // 狄克斯特拉算法
  56. function dekesitela(json_obj, json_cost, json_parent, arr) {
  57.   let node = find_lowest_cost_node(json_cost, arr)
  58.   //仍有需要处理的节点
  59.   while (node != null) {
  60.     for (let json_obj_node in json_obj[node]) {
  61.       //到达当前节点开销+邻近节点开销 < 之前记录的开销
  62.       if (json_cost[node] + json_obj[node][json_obj_node] < json_cost[json_obj_node]) {
  63.         costs[json_obj_node] = json_cost[node] + json_obj[node][json_obj_node]
  64.         json_parent[json_obj_node] = node
  65.       }
  66.     }
  67.     // 已经检查过的最低权重元素放在数组
  68.     arr.push(node)
  69.     node = find_lowest_cost_node(json_cost, arr)
  70.   }
  71. }
  72. dekesitela(graph, costs, parents, processed)
  74. console.log(processed)//