重要概念
变量 = 节点 = 顶点
因果推断是个科学发现问题,所以随机变量是最基本的概念。在因果图中,变量以节点或顶点的形式存在。
在其他图工具中,一般是先构建图,然后再填入节点。如果图不存在了节点也随之消失。与这些图工具不同,我们将节点视为基本对象。 你可以用同一组节点构建多个图。这与我们处理科学问题的思路一致:先知晓变量,然后从中获得因果关系。
变量可以是离散值也可以是连续值,不同数值类型对应不同的搜索算法。
当导入数据时变量会自动创建,或者手动创建图时手动创建变量。
数据集
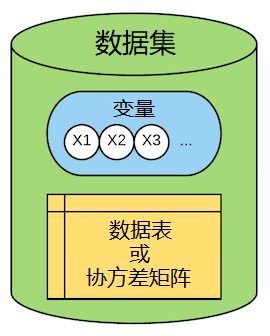
数据集分为2部分:第一部分是变量集合 $V$,第二部分是这些变量的观测值集合 $X$ 或这些变量的协方差矩阵 $\Sigma$。
数据集在导入数据时创建。
图
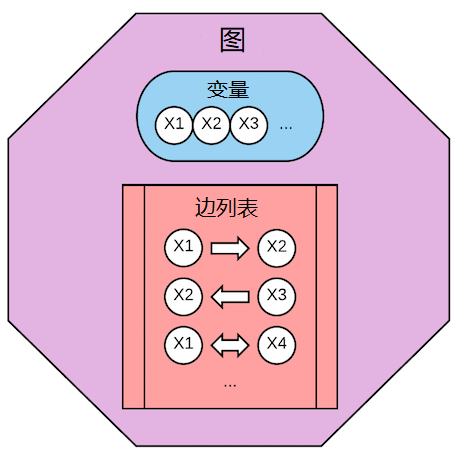
图 $G$ 由节点集合 $V$ 和边集合 $E$ 组成。每条边有4部分信息:一对节点和一对端点。 例如边 $(A, B, -, >)$ 表示 $A \rarr B$,边 $(B, C, >, >)$ 表示 $B \leftrightarrow C$ 。 这使得图的表示非常灵活:既可以表示无向边,也可以表示双向边,甚至一些特殊边。 边 $A \rarr B$ 也以描述为“A对B存在直接因果效应”。
背景知识
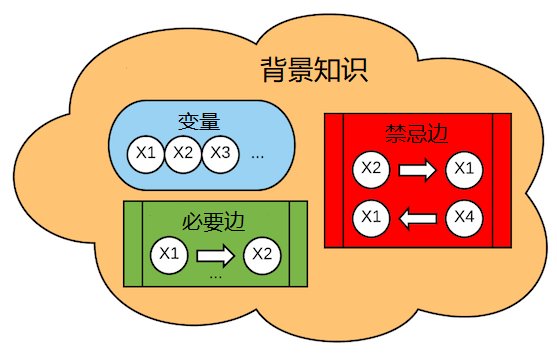
在因果发现算法中,往往需要背景知识(先验知识)作为输入辅助搜索。 背景知识由一组变量、禁忌边列表和必要边列表组成。
构建背景知识时你可以将背景知识视为独立内容—这也就是为什么称其为背景知识。 但是背景知识不能脱离输入的变量,只有这样才能建立禁忌边和必要边,也就是“关于什么的知识”。
搜索算法
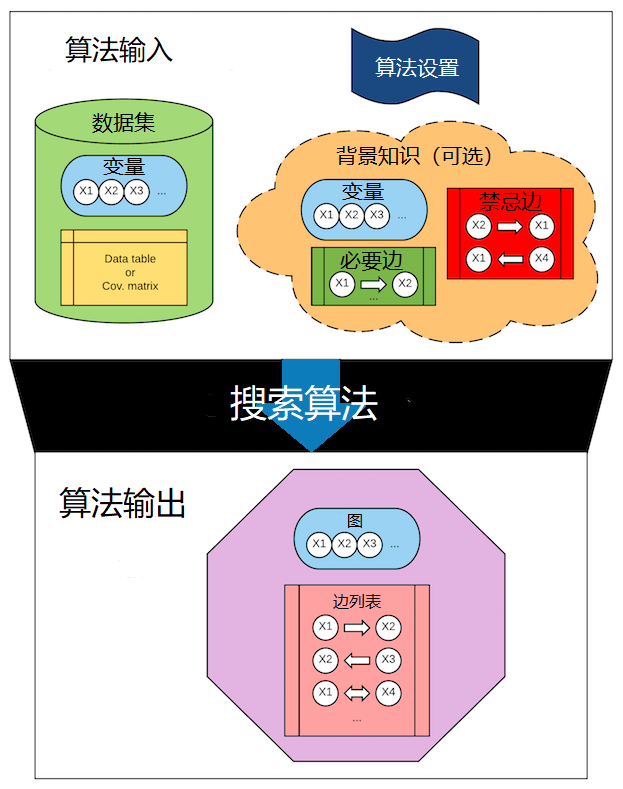
因果发现问题可以简单理解为,首先我们有一组变量,然后在这些变量能组成的 所有 图中,找到一个能够正确描述这些变量之间因果关系的图。
到底要搜索多少图呢?
| 变量数 | 有向无环图数 |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 25 |
| 4 | 543 |
| 5 | 29281 |
| 6 | 3781503 |
| … | … |
| 20 | 超过宇宙中原子的数量 |
这就是为什么我们需要一个算法来搜索,而不是人眼来检查。搜索算法会用很多技巧快速找到答案,不会一个一个图去分析。
搜索算法是一个函数,有对应的输入和输出。输入项为:
- 数据集(必选)
- 背景知识
- 算法设置,不同算法设置参数不同
输出为一个图或与数据相容的一组图(也叫图的“等价类”)。图的类型根据算法不同而不同。
参数化模型和实例化模型
概率图只能给我们定性信息,它回答变量之间的因果影响,但不会告诉我们定量的因果效应有多大。 他们对图中变量的概率分布施加约束,但不会完全指定概率分布。因此我们需要模型。
因果模型向图中添加这些缺失的信息:模型指定概率分布,如果我们对某些变量施加干预可以得到其概率分布。
模型适用于如下几个不同任务:
- 给定我们确信的图和数据,我们可以你和模型学习因果效应的大小;
- 给定我们想要评估的图和数据,我们可以训练并测试模型来衡量图对数据描述的质量;
- 给定图,我们可以指定模型来生成该图的模拟数据,用于评估搜索搜索算法。
有两类令人混淆的模型,他们的区别整理在下表:
| 贝叶斯模型(Bayes Model) | 结构方程模型(SEM) | |
|---|---|---|
| 参数化模型 | 图(DAG)中的节点是离散变量,每个变量有一组可选值 | 图(DAG)中的节点是连续变量(均值和方差以初始化但未赋值),外加一系列线性参数(系数已初始化但未赋值) |
| 实例化模型 | 根据图中每个变量的父节点,给每个变量赋予其可能值的概率 | 值赋给线性结构方程所有参数(均值、方差和边系数) |
我们区分参数化模型和实例化模型。参数模型只是 初始化 对象,这里我们决定用哪种模型(贝叶斯还是结构方程模型)。 然后实例化模型对模型参数赋值。
贝叶斯参数化模型和实例化模型
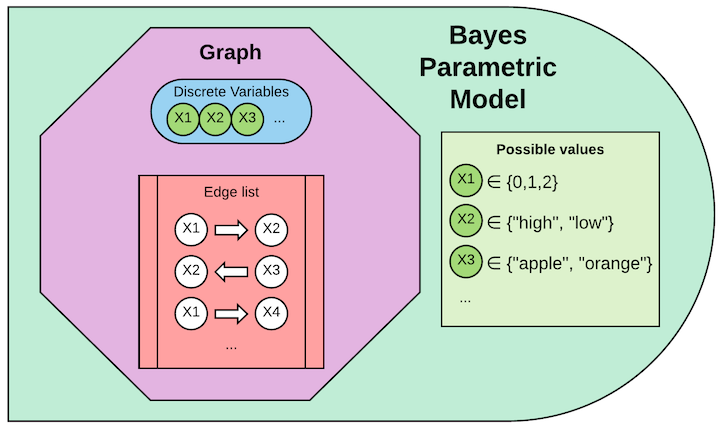
“贝叶斯模型” 仅意味着模型适配 离散数据。他与贝叶斯推断没有特殊关系。这里用“贝叶斯模型”仅仅是因为处理离散数据的DAG被称为“贝叶斯网络”。
一个贝叶斯参数化模型对象包含一个图、图中每一个变量的可选值。图必须是有向无环图(DAG)。
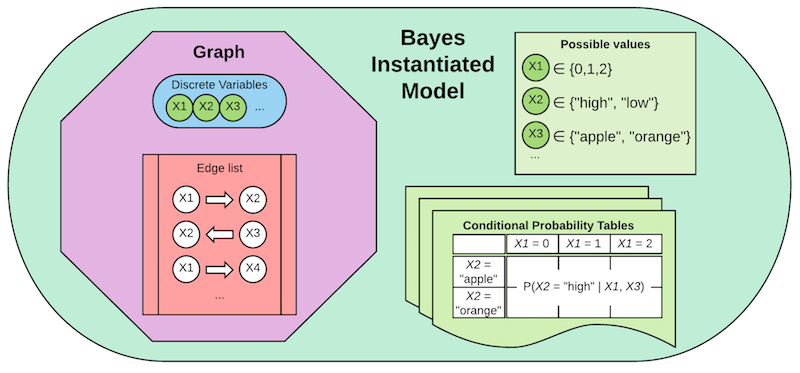
一个贝叶斯实例化模型对象包含贝叶斯参数化模型的一切,外加一组条件概率表—每张表对应一个节点,基于图中它的父节点。
结构方程参数化和实例化模型
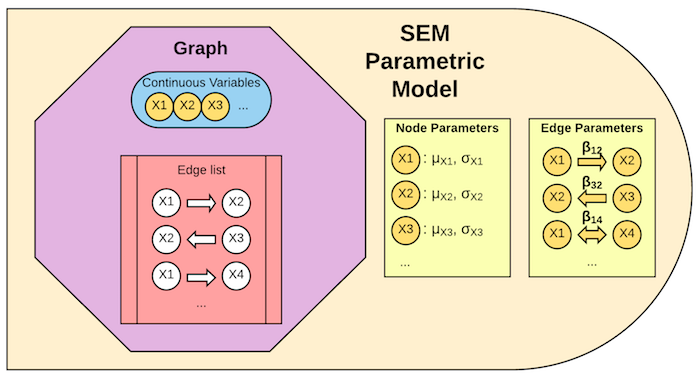
结构方程模型用于在某种变量间关系假设下拟合连续数据。既可以拟合标准结构方程模型也可以拟合广义结构方程模型。
线性模型意味着变量间的关系可以用线性方程描述。例如,假设我们有图 $\mathit{X \rarr Y \larr Z}$,我们可以将其描述为标准参数化结构方程模型:
$\mathit{X = \epsilon_1}$
$\mathit{Z = \epsilon_2}$
$\mathit{Y = \alpha X + \beta Z + \epsilon_3}$
其中$\epsilon_1, \epsilon_2, \epsilon_3$是满足高斯分布的独立随机变量。
结构方程参数化模型包含一个图,外加需要指定概率分布的所有变量的列表。在上面的例子中,参数是 $\mathit{\alpha, \beta, \mu{\epsilon1}, \mu{\epsilon2}, \mu{\epsilon3}, \sigma{\epsilon1}, \sigma{\epsilon2}, \sigma{\epsilon3}}$。 然而在结构方程参数化模型对象中,这些参数的值是待定的;这些值通过实例化模型指定(见实例化模型)。
如果选择广义结构方程参数化模型,你可以指定父子变量间的非线性关系,并且每个变量可以是非高斯分布的。 例如你可以指定某个变量与其父变量满足二次方程关系:$\mathit{Y = \alpha X + \beta X^2 + \epsilon}$。 你可以指定误差项$\epsilon$具有均匀(0, 1)分布。
注意:尽管广义结构方程模型相比标准结构方程给了你更大的自由,同时也需要你做更多的约束。你必须给出分布的参数化形式,否则无法通过数据训练出模型。 目前没有非参数化模型拟合方法。
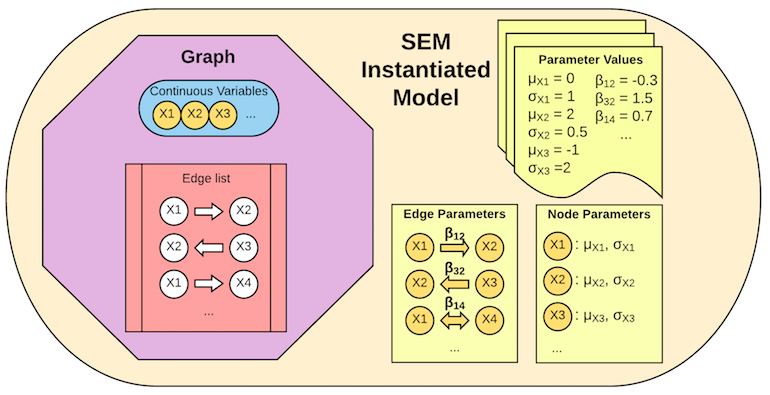
结构方程实例化模型为所有参数赋值—在上面的例子中,需要给参数$\mathit{\alpha, \beta}$赋值,同时给出误差项$\mathit{\epsilon}$的均值和方差。

