1. 什么是数学？

人类在探索每一个科学问题的时候，为了简化问题，都会把具体科学问题看作一个机器。给这个机器输入一个条件，机器会运转，对条件进行加工，然后输出一种现象。
通过研究输入与输出，有时候可以推测出机器内部的构造，这就是所谓的科学。比如牛顿，他发现：给物体一个力，就能使物体产生一个加速度，力越大，加速度就越大。
当然，有时候研究了输入与输出，依然没有搞清楚机器的内部原理，只是知道一个大概的规律，那么就干脆先不管内部原理，先把这个规律为自己所用。这就是所谓的工程。比如人们通过做实验发现，给机翼一个气流，机翼就能够产生一个升力，人们并不能解释升力是怎么产生的，但是不妨碍自己使用，于是给一个驾驶舱装上两个翅膀，飞机就上天了。

人类探索自然运行的原理，归根结底是想利用这些原理，对万物进行定量控制。

定量控制的意思是说：牛顿写出《自然定律》这个论文的时候，不能含糊其辞的说，给物体很大的力，物体就能产生很大的加速度。而是必须告诉大众：给一个多少Kg的物体多少N的力就能够产生多少的加速度。
这时候，数学应运而生。简而言之，数学就是人类在解释这个世界是怎样运行的时候，人为发明的一种工具，有了这种工具，我们可以不用那么含糊其辞。
于是就有了函数。
于是就有了：,于是就有了各种各样的公式、定理和定律。

2. 什么是线性代数？

线性代数是数学的一个分支，它的研究对象是向量，向量空间（或称线性空间），线性变换和有限维的线性方程组。向量空间是现代数学的一个重要课题；因而，线性代数被广泛地应用于抽象代数和泛函分析中；通过解析几何，线性代数得以被具体表示。线性代数的理论已被泛化为算子理论。由于科学研究中的非线性模型通常可以被近似为线性模型，使得线性代数被广泛地应用于自然科学和社会科学中。
函数研究的是，输入一个数，经过函数运算之后，产生另一个数。而有时候我们研究的问题太复杂，需要输入很多个数，经过运算之后，产生出很多个数。这个时候线性代数应运而生。
很多个数，我们可以用括号括起来，形成一个数组。在几何学上，数组被称作向量，向量就是一个有大小有方的
直线段。
所以，线性代数就是：输入一段直线，经过加工1之后，产生出另一段直线。线性的意思就是，你往机器里扔进去是直线，出来的肯定也是直线。
当然，在数学上，线性有着极其严格的定义，并不是刚刚说的那么简单。不过，正由于线性的与函数相类似，用图描述线性代数就是：
输入叫向量，内部原理叫矩阵，输出叫向量

3. 矩阵是怎么对直线进行加工的？

通过函数表达式我们可以一目了然地知道，输入的自变量是怎么一步步被加工，最后输出因变量的。
同样，通过观察矩阵，我们也可以一目了然地知道，输入的直线是怎样一步步被加工的。
假如输入的直线为[1,2]。

向量[1,2]的全称其实是,i和j叫做基向量。意思是说，我们目前所写出来的向量，是以这两个向量作为基本原料，拼凑出来的。

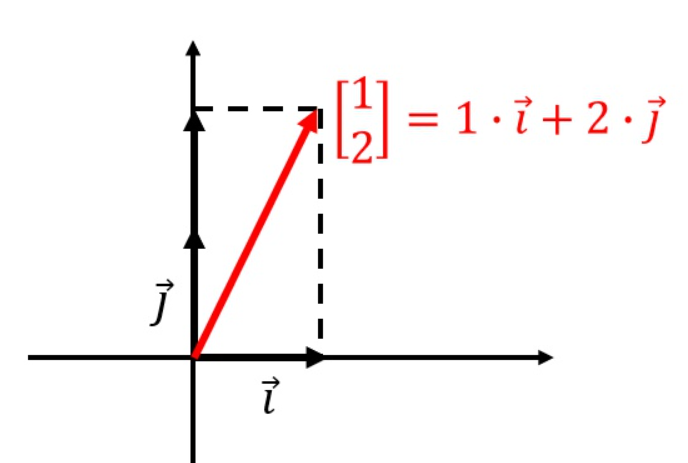
假如用于加工向量的矩阵为,那么这个矩阵所代表的加工过程就是，把基向量i，换成矩阵中的第一列，把基向量j换成矩阵中的第二列。然后再以新的基向量为原料，重新利用[1,2]拼凑一个新的向量。用新的基向量拼凑出来的新向量就是输出。

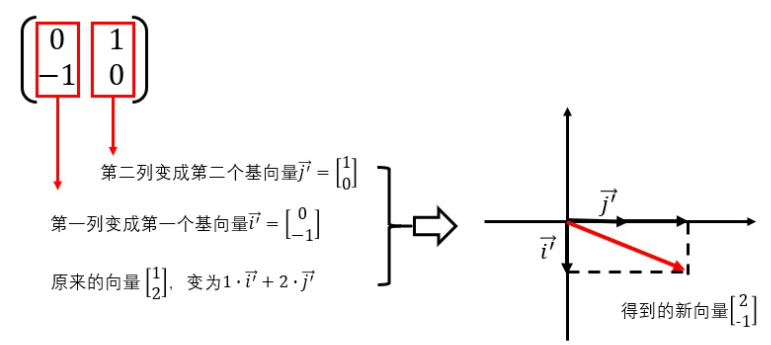
通过展示矩阵对向量的加工过程，我们可以看出上面例子的解。
下面，我们用熟悉的口诀”左行乘右列“来检查一下上面的答案是否正确

其实，计算所用的口诀就来源于上述加工过程。
同理，稍微复杂一点的三维向量遇到三维矩阵后的加工过程如下图：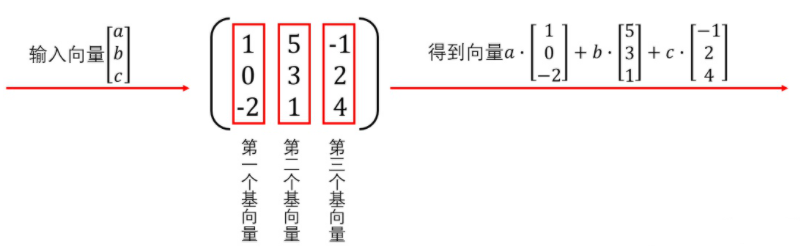

4. 什么是行列式？

矩阵对向量进行加工，行列式能够描述这种加工的强弱
上文提到，矩阵对向量加工是通过改变基向量来实现的，以二维为例，默认的基向量张成的面积为1，经过矩阵变换之后形成的新的基向量张成面积变成了S,那么这个矩阵的行列式就是S.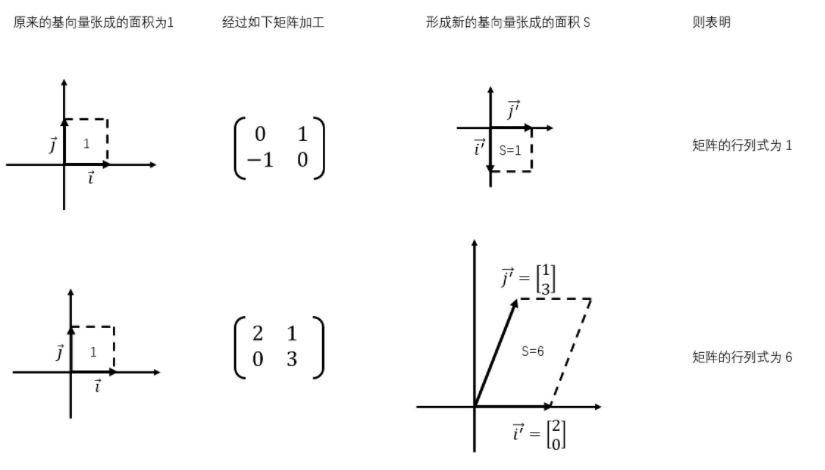

有时候，矩阵的行列式为0，说明新的基向量张成的面积为0，说明新的基向量发生了重合。
有时候，矩阵的行列式为负数，说明线性空间发生了翻转。也就是说，本来，默认的两个基向量，j在i的逆时针方向，经过矩阵加工之后，线性空间发生了翻转，导致i在j的逆时针方向。如下图：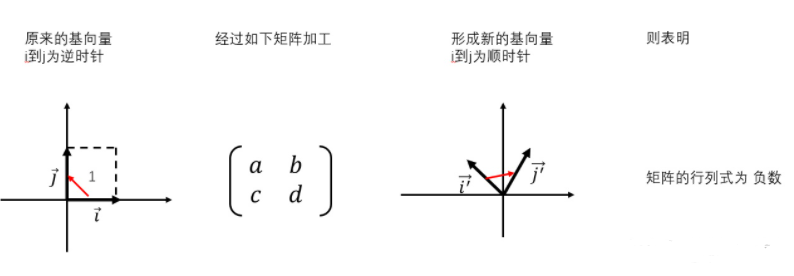

5. 什么是单位矩阵？

矩阵能够对向量进行加工，产生一个新的向量。但有一种矩阵比较特殊，无论给它输入什么样的向量，加工之后产生的向量都与原来的相同，这种矩阵叫做单位矩阵。
既然矩阵度对向量的加工作用是通过改变基向量来实现的，如果想保持输入与输出相等，那么只需要保证矩阵不会改变基向量即可。
所以，二阶单位矩阵，三阶单位矩阵以及n阶单位矩阵可写为：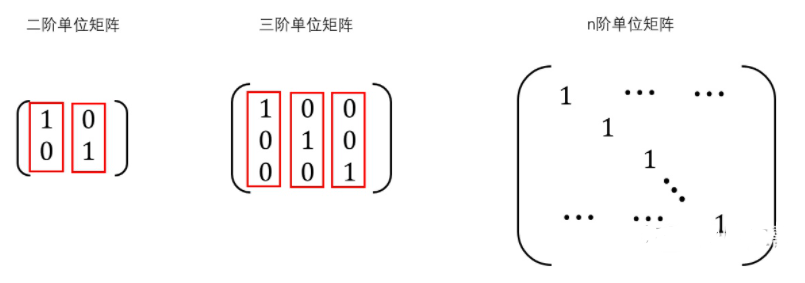

6. 什么是逆矩阵？

矩阵对向量具有加工作用，两个矩阵相乘，则表示的是两种加工作用的叠加。也就是说：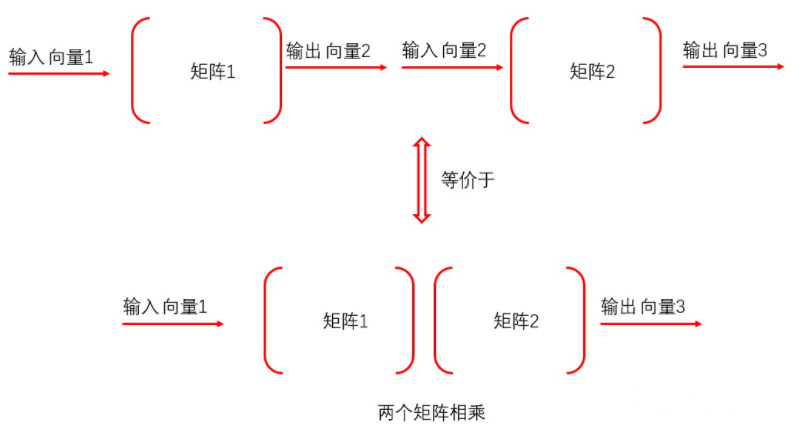

如果上图中向量1等于向量3，那么就说明，向量经过矩阵1和矩阵2的加工之后，又变成了原来的自己。进一步说明，矩阵1和矩阵2对于向量的加工作用刚好相反。那么就说明矩阵1和矩阵2互为逆矩阵。
明白了原理，也就知道如何求解逆矩阵了。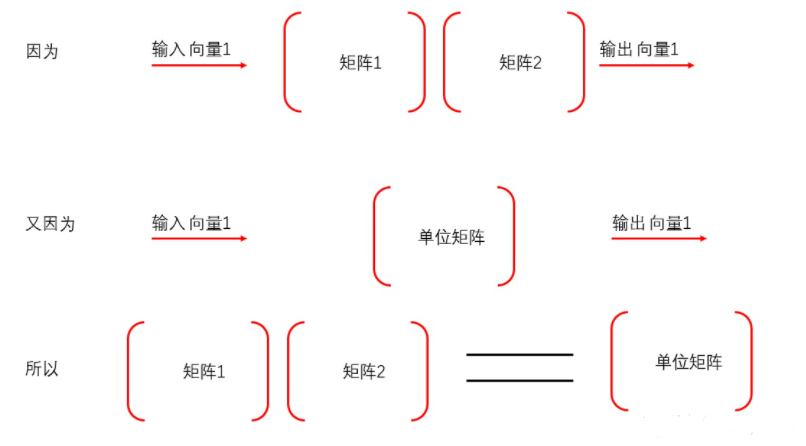

为什么行列式0的矩阵没有逆矩阵？ 因为行列式如果为0，表明矩阵在对向量变换的过程中，将向量空间压缩到了一个更低的维度上。以二维矩阵为例：

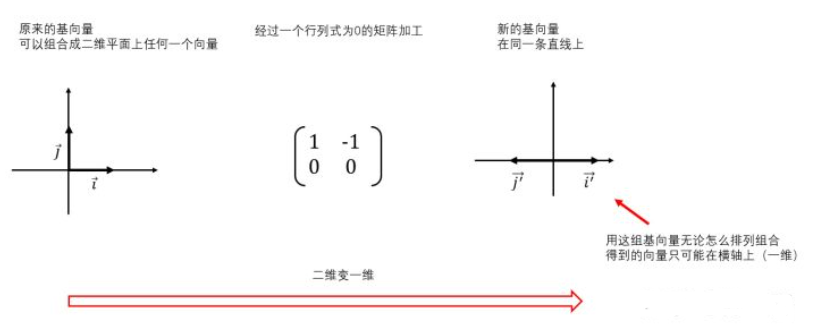
向量降维后，将无法还原到原来的样子。
就比如说一个三维长方体，从大部分角度观察，都是一个三维结构，但是当正视俯视侧视时，你只能观察到一个二维矩形。我们是无法单独通过一个二维矩形的样子，来推测出原来的长方体的

7. 什么是秩？

矩阵可以将一个向量进行加工，变成另外一个向量。
比如一个三阶矩阵，可以对很多三维向量进行加工，变成很多新的三维向量。
有时候，所有的这些新的三维向量，最终都落在一条直线上，即一维；
有时候，所有新的三维向量最终都落在一个二维平面上，即二维；
有时候所有新的三维向量最终都落在三维空间上，即三维。
以上情况分别对应于秩为1,2,3.
总之，秩就是描述这个矩阵会不会将输入的向量空间降维。如果没有降维，这种情况呗称为满秩。

8. 什么是特征向量、特征值？

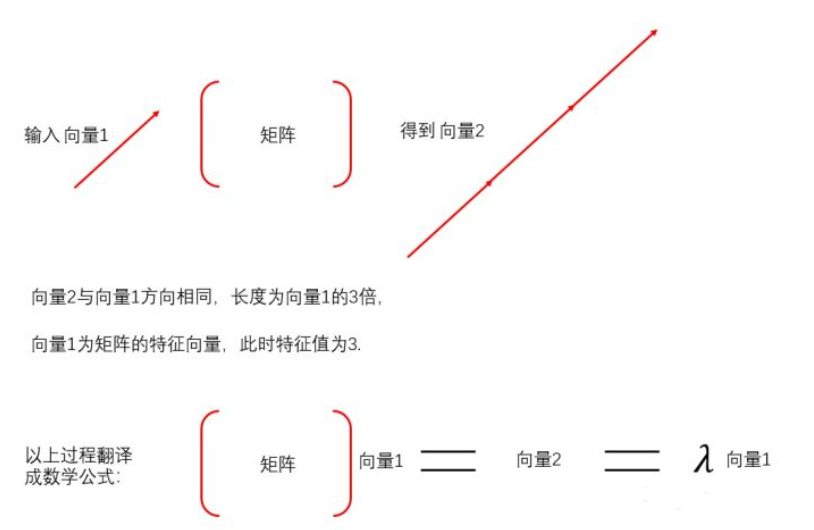
矩阵能够对向量进行加工，变成一个新的向量。
有时候会出现这种情况：
对于某一个矩阵，输入一个向量，经过矩阵加工后，新生成的向量与原来的向量共线。也就是说这个矩阵对这个特定的向量的加工过程中没有改变其方向。
那么，这个不会被改变方向的向量叫做这个矩阵的特征向量。
虽然不会被改变方向，但是改变了大小，新的向量长度是原来的向量长度的倍，这个叫做特征向量的特征值。

想学习更多的数学知识，强烈推荐关注Bilibili:3Blue1Brown的官方账号，深入浅出、直观明了地分享数学之美。