1、链表

使用一个链表管理类实现链表的增加、删除等功能，这其中用到了递归

  1. /**
  2.     链表
  3.     一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，
  4.     而是在每一个节点里存到是下一个节点的指针(Pointer）。
  6.     链表与数组：线性数据结构
  8.     数组适合查找，遍历，固定长度
  9.     链表适合插入，删除，不宜过长，否则会导致遍历性能下降
  11. */
  12. public class Test15{
  13.     public static void main(String[] args){
  15.         NodeManager nm = new NodeManager();
  16.         System.out.println("------add----------");
  17.         nm.add(5);
  18.         nm.add(4);
  19.         nm.add(3);
  20.         nm.add(2);
  21.         nm.add(1);
  22.         nm.print();
  23.         System.out.println("-------del---------");
  24.         nm.del(3);
  25.         nm.print();
  26.         System.out.println("-------find---------");
  27.         System.out.println(nm.find(1));
  28.         System.out.println("-------update---------");
  29.         nm.update(1,10);
  30.         nm.print();
  31.         System.out.println("-------insert---------");
  32.         nm.insert(1,20);
  33.         nm.print();
  35.     }
  36. }
  38. class NodeManager{
  39.     private Node root;//根节点
  40.     private int currentIndex = 0;//节点的序号，每次操作从0开始
  42.     //添加
  43.     public void add(int data){
  44.         if(root==null){
  45.             root = new Node(data);
  46.         }else{
  47.             root.addNode(data);
  48.         }
  49.     }
  50.     //删除
  51.     public void del(int data){
  52.         if(root==null)return;
  53.         if(root.getData()==data){
  54.             root = root.next;
  55.         }else{
  56.             root.delNode(data);
  57.         }
  58.     }
  59.     //打印所有
  60.     public void print(){
  61.         if(root!=null){
  62.             System.out.print(root.getData()+"->");
  63.             root.printNode();
  64.             System.out.println();
  65.         }
  66.     }
  67.     //查找是否存在节点
  68.     public boolean find(int data){
  69.         if(root==null)return false;
  70.         if(root.getData()==data){
  71.             return true;
  72.         }else{
  73.             return root.findNode(data);
  74.         }
  75.     }
  76.     //更新
  77.     public boolean update(int oldData,int newData){
  78.         if(root==null)return false;
  79.         if(root.getData()==oldData){
  80.             root.setData(newData);
  81.             return true;
  82.         }else{
  83.             return root.updateNode(oldData,newData);
  84.         }
  85.     }
  86.     //向索引之前插入
  87.     public void insert(int index,int data){
  88.         if(index<0)return;
  89.         currentIndex = 0;    //节点序号
  90.         if(index==currentIndex){
  91.             Node newNode = new Node(data);
  92.             newNode.next = root;
  93.             root = newNode;
  94.         }else{
  95.             root.insertNode(index,data);
  96.         }
  97.     }
  100.     private class Node{
  101.         private int data;
  102.         private Node next; //把当前类型作为属性
  103.         public Node(int data){
  104.             this.data = data;
  105.         }
  106.         public void setData(int data){
  107.             this.data = data;
  108.         }
  109.         public int getData(){
  110.             return data;
  111.         }
  112.         //添加节点
  113.         public void addNode(int data){
  114.             if(this.next==null){
  115.                 this.next = new Node(data);
  116.             }else{
  117.                 this.next.addNode(data);
  118.             }
  119.         }
  120.         //删除节点
  121.         public void delNode(int data){
  122.             if(this.next!=null){
  123.                 if(this.next.data==data){
  124.                     this.next = this.next.next;
  125.                 }else{
  126.                     this.next.delNode(data);
  127.                 }
  128.             }
  129.         }
  130.         //输出所有节点
  131.         public void printNode(){
  132.             if(this.next!=null){
  133.                 System.out.print(this.next.data+"->");
  134.                 this.next.printNode();
  135.             }
  136.         }
  137.         //查找节点是否存在
  138.         public boolean findNode(int data){
  139.             if(this.next!=null){
  140.                 if(this.next.data==data){
  141.                     return true;
  142.                 }else{
  143.                     return this.next.findNode(data);
  144.                 }
  145.             }
  146.             return false;
  147.         }
  148.         //修改节点
  149.         public boolean updateNode(int oldData,int newData){
  150.             if(this.next!=null){
  151.                 if(this.next.data==oldData){
  152.                     this.next.data = newData;
  153.                     return true;
  154.                 }else{
  155.                     return this.next.updateNode(oldData,newData);
  156.                 }
  157.             }
  158.             return false;
  159.         }
  160.         //插入节点
  161.         public void insertNode(int index,int data){
  162.             currentIndex++;
  163.             if(index==currentIndex){
  164.                 Node newNode = new Node(data);
  165.                 newNode.next = this.next;
  166.                 this.next = newNode;
  167.             }else{
  168.                 this.next.insertNode(index,data);
  169.             }
  170.         }
  171.     }
  172. }
  1. ------add----------
  2. 5->4->3->2->1->
  3. -------del---------
  4. 5->4->2->1->
  5. -------find---------
  6. true
  7. -------update---------
  8. 5->4->2->10->
  9. -------insert---------
  10. 5->20->4->2->10->

在链表管理类中写一个方法实现链表反转、以及链表自身的打印全部

  1. public class Test17 {
  2.     public static void main(String[] args) {
  3.         ListNode n1=new ListNode(1);
  4.         ListNode n2=new ListNode(2);
  5.         ListNode n3=new ListNode(3);
  6.         ListNode n4=new ListNode(4);
  8.         ListNodeManage ls=new ListNodeManage();
  9.         ls.println();
  11.         System.out.println("----------------");
  12.         ls.add(n1);
  13.         ls.add(n2);
  14.         ls.add(n3);
  15.         ls.add(n4);
  16.         ls.println();
  18.         System.out.println("----------------");
  19.         ListNode listNode = ls.reverseNode(n2);
  20.         listNode.showNodes();
  21.     }
  22. }
  23. class ListNodeManage{
  24.     private ListNode root;
  26.     public ListNode reverseNode(ListNode node){
  27.         ListNode res=null;
  28.         ListNode n=null;
  29.         while(node!=null){
  30.             n=node.getNext();
  31.             node.setNext(res);
  32.             res=node;
  33.             node=n;
  34.         }
  35.         return res;
  36.     }
  38.     public void println(){
  39.         if(root==null){
  40.             System.out.println("链表为空");
  41.         }else{
  42.             System.out.println(root);
  43.             root.printNode();
  44.         }
  45.     }
  47.     public void add(ListNode node){
  48.         if(root==null){
  49.             root=node;
  50.         }else {
  51.             root.addNode(node);
  52.         }
  53.     }
  55.     @Override
  56.     public String toString() {
  57.         return "ListNodeManage{" +
  58.                 "root=" + root +
  59.                 '}';
  60.     }
  61. }
  65. class ListNode{
  66.     private int val;
  67.     private ListNode next;
  69.     public void showNodes(){
  70.         System.out.println(this);
  71.         this.showNextNode();
  72.     }
  73.     private void showNextNode(){
  74.         if(this.next!=null){
  75.             System.out.println(this.next);
  76.             this.next.showNextNode();
  77.         }
  78.     }
  80.     public void printNode(){
  81.         if(this.next!=null){
  82.             System.out.println(this.next);
  83.             this.next.printNode();
  84.         }
  85.     }
  87.     public void addNode(ListNode node){
  88.         if(this.next==null){
  89.             this.next=node;
  90.         }else{
  91.             this.next.addNode(node);
  92.         }
  93.     }
  95.     @Override
  96.     public String toString() {
  97.         return "ListNode{" +
  98.                 "val=" + val +
  99.                 '}';
  100.     }
  102.     public ListNode(int val) {
  103.         this.val = val;
  104.     }
  106.     public ListNode() {
  107.     }
  109.     public int getVal() {
  110.         return val;
  111.     }
  113.     public void setVal(int val) {
  114.         this.val = val;
  115.     }
  117.     public ListNode getNext() {
  118.         return next;
  119.     }
  121.     public void setNext(ListNode next) {
  122.         this.next = next;
  123.     }
  124. }
  1. 链表为空
  2. ----------------
  3. ListNode{val=1}
  4. ListNode{val=2}
  5. ListNode{val=3}
  6. ListNode{val=4}
  7. ----------------
  8. ListNode{val=4}
  9. ListNode{val=3}
  10. ListNode{val=2}
  12. Process finished with exit code 0

删除链表中的某个元素

  1. package com.chang;
  3. public class test {
  4.     public static void main(String[] args) {
  5.         listNode li1=new listNode(2);
  6.         listNode li2=new listNode(1);
  7.         listNode li3=new listNode(5);
  8.         listNode li4=new listNode(9);
  9.         li1.next=li2;
  10.         li2.next=li3;
  11.         li3.next=li4;
  12. //        printInfo(li1);
  13.         int val=1;
  14.         listNode root=new listNode(-1);
  15.         listNode pre=root;
  16.         listNode cur=li1;
  17.         while(cur!=null){
  18.             if(cur.val!=val){
  19.                 pre.next=cur;
  20.                 pre=pre.next;
  21.                 cur=cur.next;
  22.             }else{
  23.                 cur=cur.next;
  24.             }
  25.         }
  26.         printInfo(root.next );
  27.     }
  29.     private static class listNode{
  30.         int val;
  31.         listNode next=null;
  32.         public listNode(int val) {
  33.             this.val = val;
  34.         }
  36.         @Override
  37.         public String toString() {
  38.             return "listNode{" +
  39.                     "val=" + val +
  40.                     '}';
  41.         }
  42.     }
  44.     private static void printInfo(listNode node){
  45.         System.out.println("打印所有节点");
  46.         while(node!=null){
  47.             System.out.println(node);
  48.             node=node.next;
  49.         }
  50.         System.out.println("--------------");
  51.     }
  52. }

2、二叉树

树是一种重要的非线性数据结构， 直观地看， 它是数据元素（在树中称为结点） 按分支关系组织起来的结构。

二叉树（Binary Tree） 是每个节点最多有两个子树的有序树。 通常子树被称作“ 左子树” 和“ 右子树”。

二叉树算法的排序规则：

  1. 选择第一个元素作为根节点
  2. 之后如果元素大于根节点放在右子树， 如果元素小于根节点， 则放在左子树
  3. 最后按照中序遍历的方式进行输出， 则可以得到排序的结果（左->根->右）

8、 3、 10、 1、 6、 14、 4、 7、 13

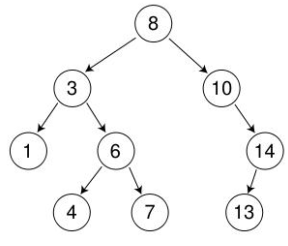
20、数据结构 - 图1

  1. public class BinaryTree {
  3.    private Node root;
  5.    //添加节点
  6.    public void add(int data){
  7.       if(root==null){
  8.          root = new Node(data);
  9.       }else{
  10.          root.addNode(data);
  11.       }
  12.    }
  13.    //输出节点
  14.    public void print(){
  15.       root.printNode();
  16.    }
  18.    private class Node{
  19.       private int data;
  20.       private Node left;
  21.       private Node right;
  22.       public Node(int data){
  23.          this.data = data;
  24.       }
  26.       public void addNode(int data){
  27.          if(this.data>data){
  28.             if(this.left==null){
  29.                this.left = new Node(data);
  30.             }else{
  31.                this.left.addNode(data);
  32.             }
  33.          }else{
  34.             if(this.right==null){
  35.                this.right = new Node(data);
  36.             }else{
  37.                this.right.addNode(data);
  38.             }
  39.          }
  40.       }
  42.       //中序遍历(先序遍历，后序遍历)
  43.       public void printNode(){
  44.          if(this.left!=null){
  45.             this.left.printNode();
  46.          }
  47.          System.out.print(this.data+"->");
  48.          if(this.right!=null){
  49.             this.right.printNode();
  50.          }
  51.       }
  52.    }
  53. }
  1. public class BinaryTreeDemo {
  3.    public static void main(String[] args) {
  5.       BinaryTree bt = new BinaryTree();
  6.       // 8、3、10、1、6、14、4、7、13
  7.       bt.add(8);
  8.       bt.add(3);
  9.       bt.add(10);
  10.       bt.add(1);
  11.       bt.add(6);
  12.       bt.add(14);
  13.       bt.add(4);
  14.       bt.add(7);
  15.       bt.add(13);
  17.       bt.print();
  18.    }
  19. }
  1. /
  2. public static int TreeDepth(BinaryTree.Node root){
  3.         if(root==null){
  4.             return 0;
  5.         }
  6.         int l=TreeDepth(root.left);
  7.         int r=TreeDepth(root.right);
  8.         return Math.max(l,r)+1;
  9.     }