二叉树特性

特性1： 第n层的二叉树最多拥有 2个节点

二叉树的每一层节点数相对于是一个比为2的等比数列。所以第n项最大为 2^(n-1)。

特性2： 深度为k的二叉树，最多有 2-1 个节点数

相对于求一个比为2的等比数列的前n项和。

特性3：叶子节点数 = 度为2的节点数 + 1

image.png

推广：m度的树，叶子节点个数为

n0 = n2 + 2n3 + 3n4 + … + (m-1)nm + 1

满二叉树

定义：一个深度为k 且 节点数 = 2- 1 的二叉树叫做满二叉树。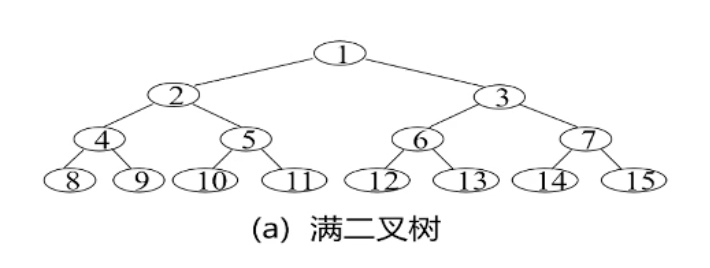
image.png

完全二叉树

定义：一棵树的已有节点顺序和满二叉树完全对应那这棵树就是完全二叉树。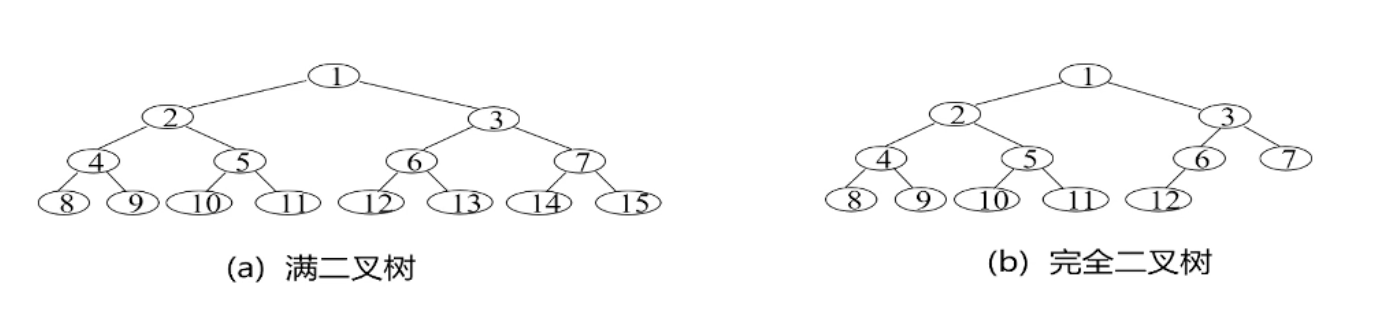
image.png
注：b虽然比a少了3个节点，但b的已有节点的编号和a完全一致，所以b是一棵完全二叉树。

完全二叉树性质

性质4

image.png

性质5

完全二叉树的所有叶子节点都在 k-1 层和 k 层 （最后两层）

性质6

完全二叉树有左节点未必有有右节点，但有右节点一定有左节点。

性质7

image.png

性质8

度为1的节点个数 <= 1

二叉树的存储

顺序结构存储

用一个数组来存储，按照编号（下标0不存储）存储。一般只有完全二叉树才使用顺序结构存储，因为非完全二叉树会浪费大量存储空间。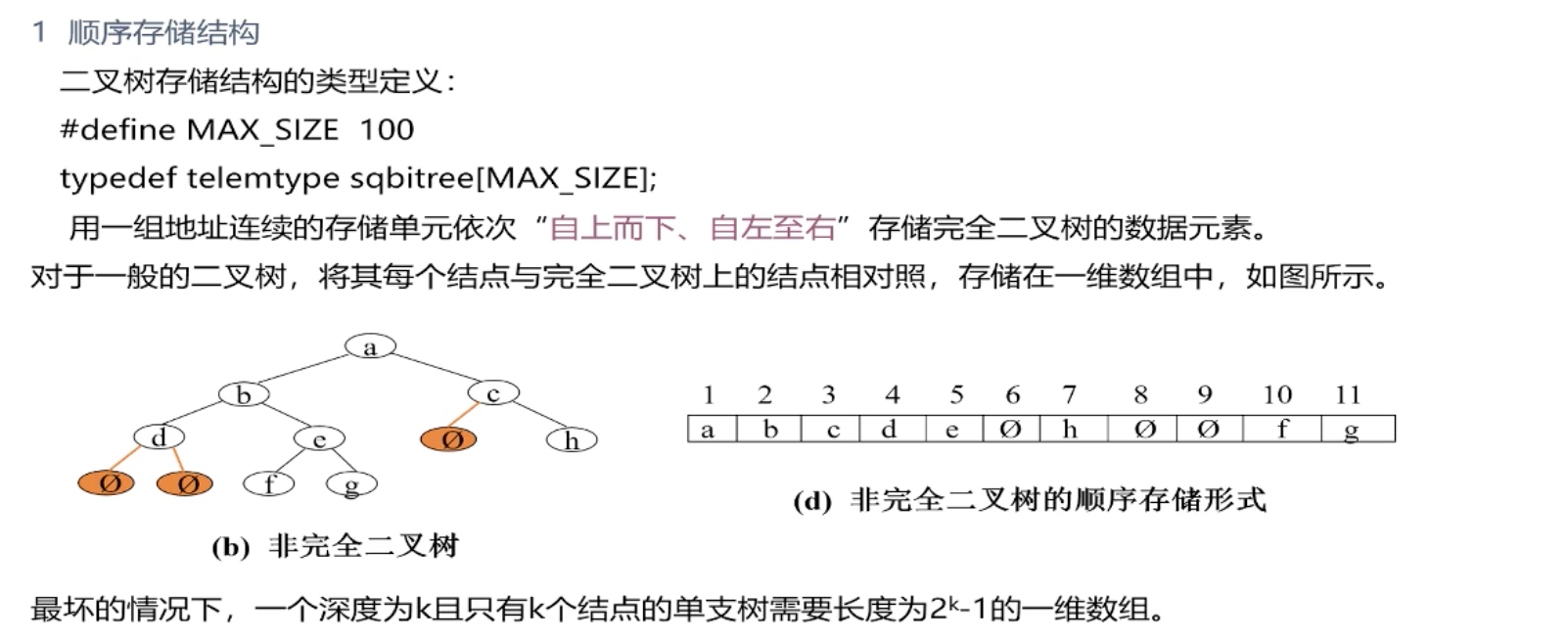
image.png

链式存储

用一个链表来存储二叉树。
image.png

视频：