算法的稳定性

即，在一个待运算的记录序列中，如果有多个相同的数，那么经过运算后任然保持运算之前的相对序列则说明该算法是稳定的。（例如：A1 = A2, 运算之前A1在A2前面，运算过后A1仍在A2前面）

稳定性的意义

1、如果只是简单的进行数字的排序，那么稳定性将毫无意义。
2、如果排序的内容仅仅是一个复杂对象的某一个数字属性，那么稳定性依旧将毫无意义（正如上面说的，会增大一定的开销，但并不起决定性因素，算法本身的开销才是关键——比如换种算法）
3、如果要排序的内容是一个复杂对象的多个数字属性，但是其原本的初始顺序毫无意义，那么稳定性依旧将毫无意义。
4、除非要排序的内容是一个复杂对象的多个数字属性，且其原本的初始顺序存在意义，那么我们需要在二次排序的基础上保持原有排序的意义，才需要使用到稳定性的算法，例如要排序的内容是一组原本按照价格高低排序的对象，如今需要按照销量高低排序，使用稳定性算法，可以使得想同销量的对象依旧保持着价格高低的排序展现，只有销量不同的才会重新排序。（当然，如果需求不需要保持初始的排序意义，那么使用稳定性算法依旧将毫无意义）。

递归

递归基本法则：

  1. 基准情形：必须总要有某些基准的情形，它们不用递归就能求解。
  2. 不断推进：对于那些要递归求解的情形，递归调用必须总能够朝着一个基准情形前进。

递归的时间复杂度计算：子问题个数*解决一个子问题需要的时间

反转链表的前N个节点

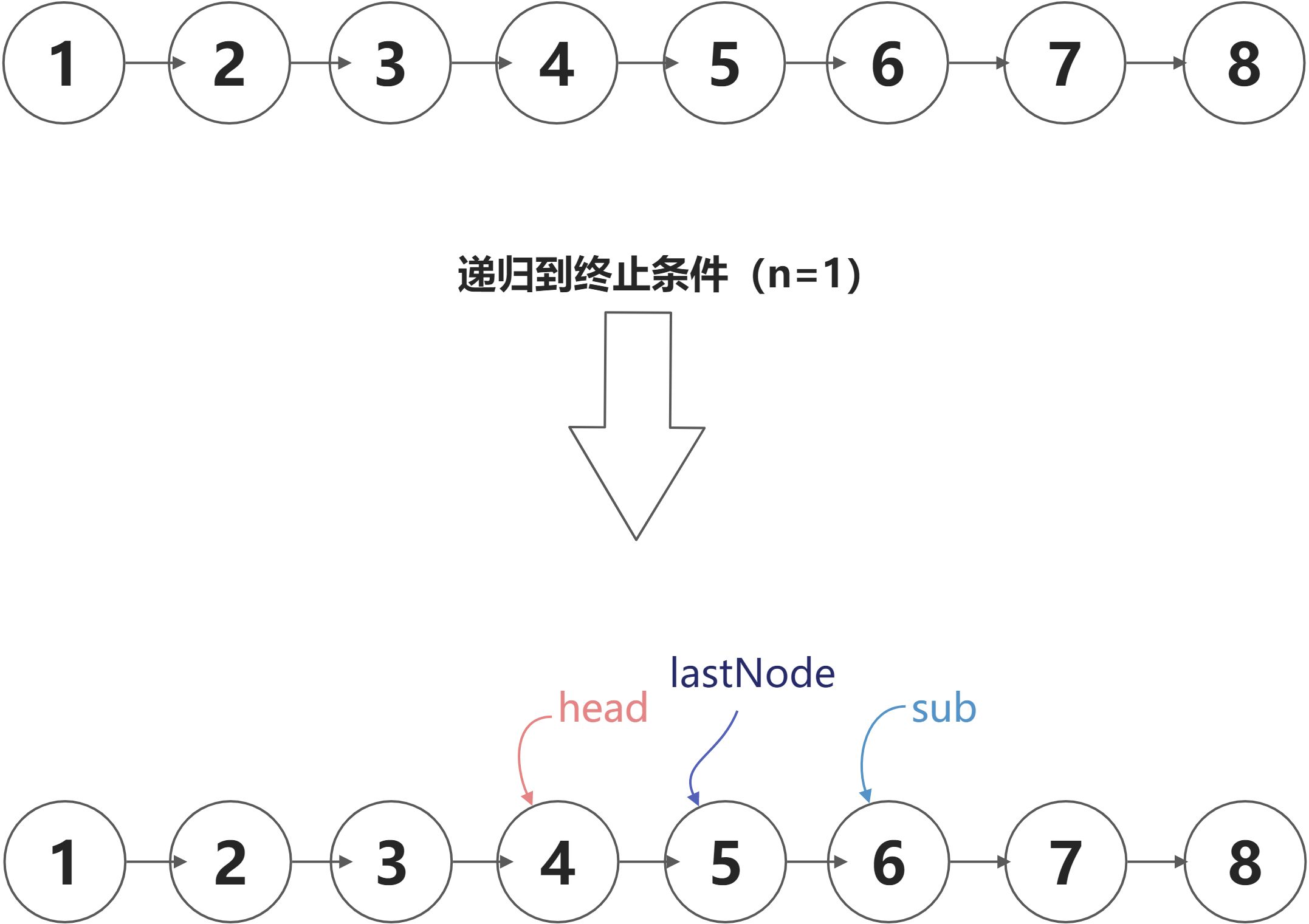
反转以head为头节点的前n个节点

  1. /**
  2.  * public class ListNode {
  3.  *     int val;
  4.  *     ListNode next;
  5.  *     ListNode() {}
  6.  *     ListNode(int val) { this.val = val; }
  7.  *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
  8.  * }
  9.  */
  10. public class ReturnList{
  12.     ListNode sub = null;
  14.     public int reverse(ListNode head, int n){
  15.         if(n == 1){
  16.             //    改写sub，获取反转后指向的下一个未反转节点
  17.             sub = head.next;
  19.             return head;
  20.         }
  21.         //    递归处理
  22.         ListNode lastNode = reverse(head.next, n-1);
  23.         //    改写该head节点的下个节点的指向下个节点的指针
  24.         head.next.next = head;
  25.         //    改写指针后使得该节点指向的下一个节点始终为未反转的节点
  26.         head.next = sub;
  28.         return lastNode;
  29.     }
  31. }

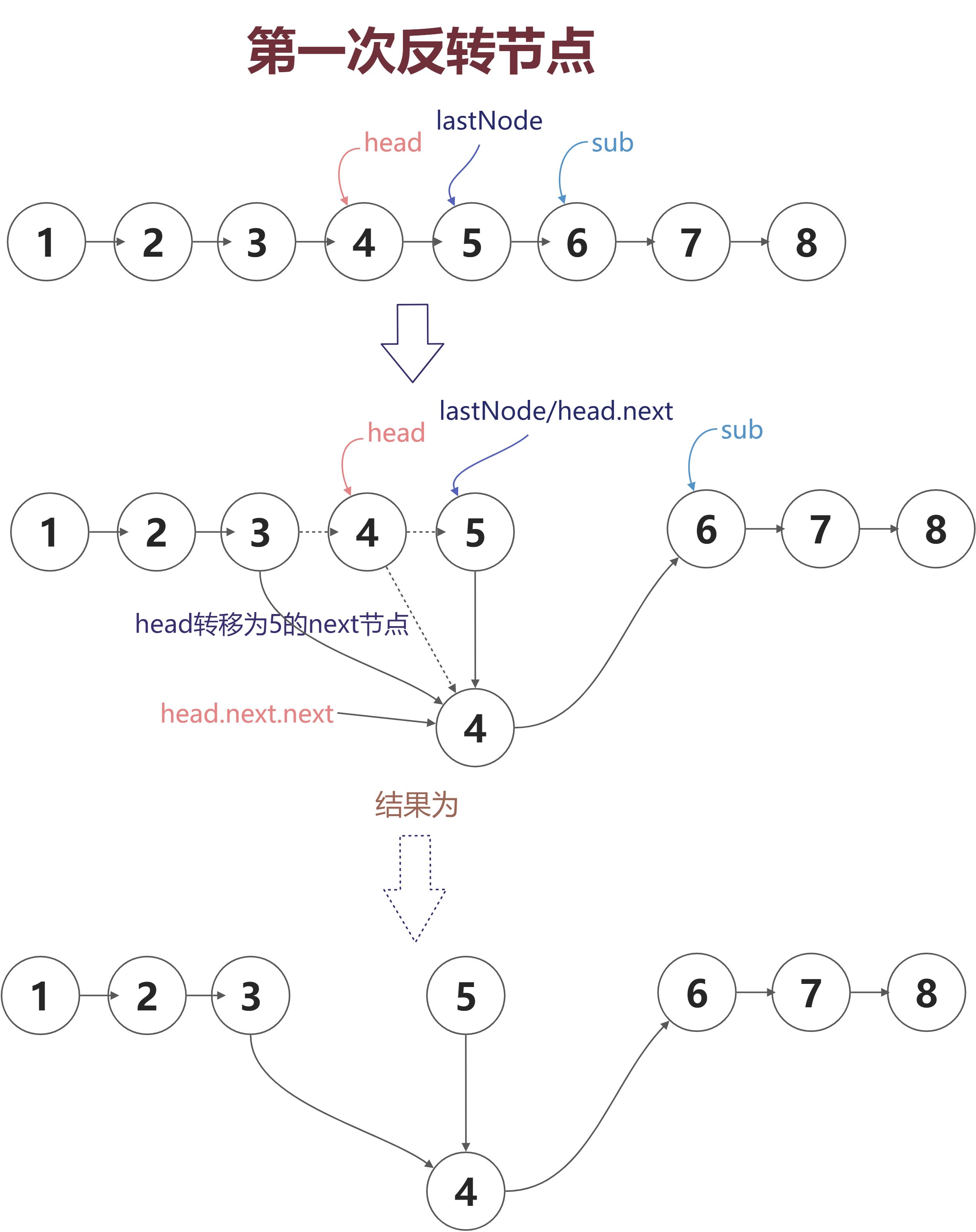
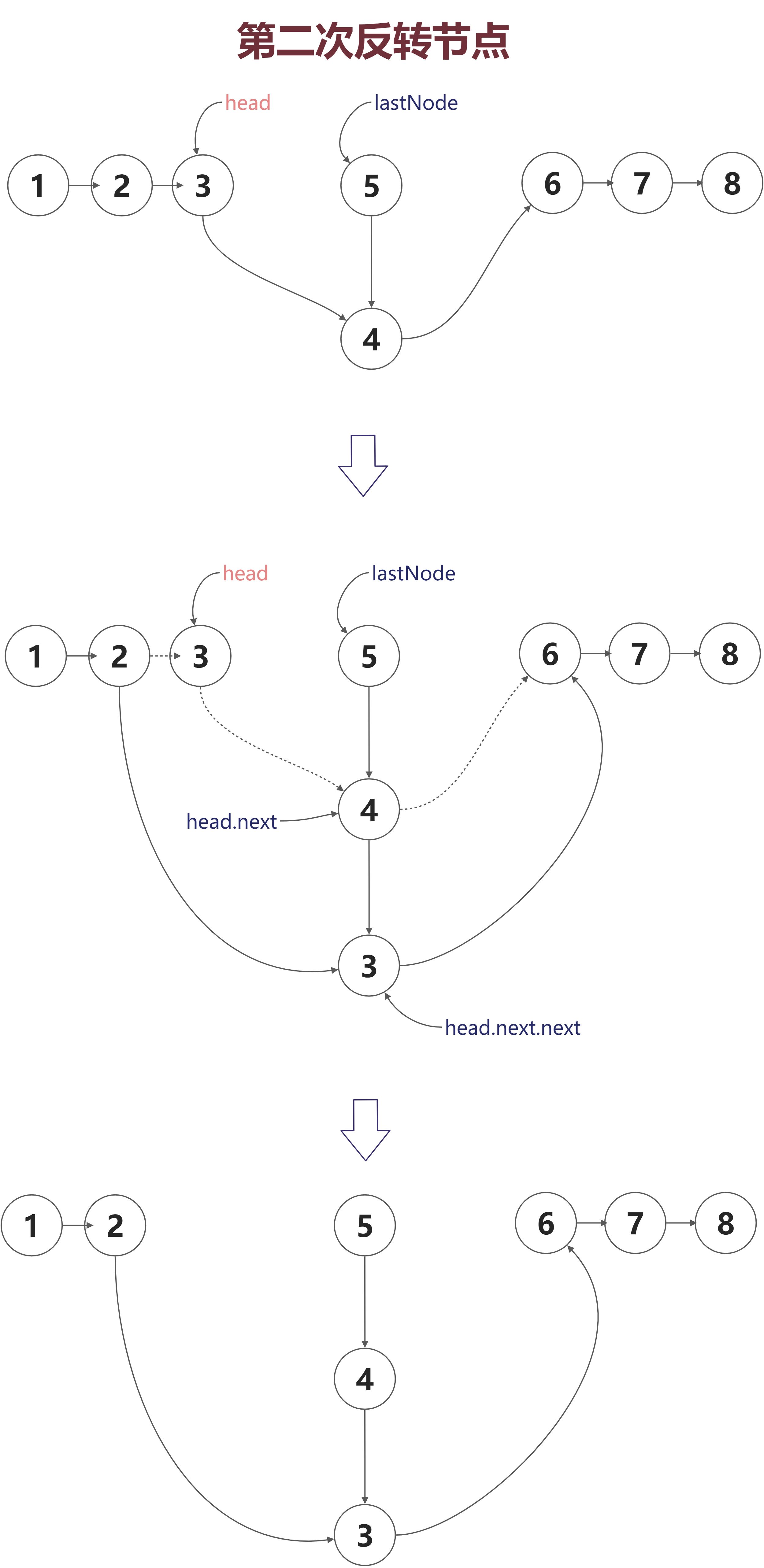
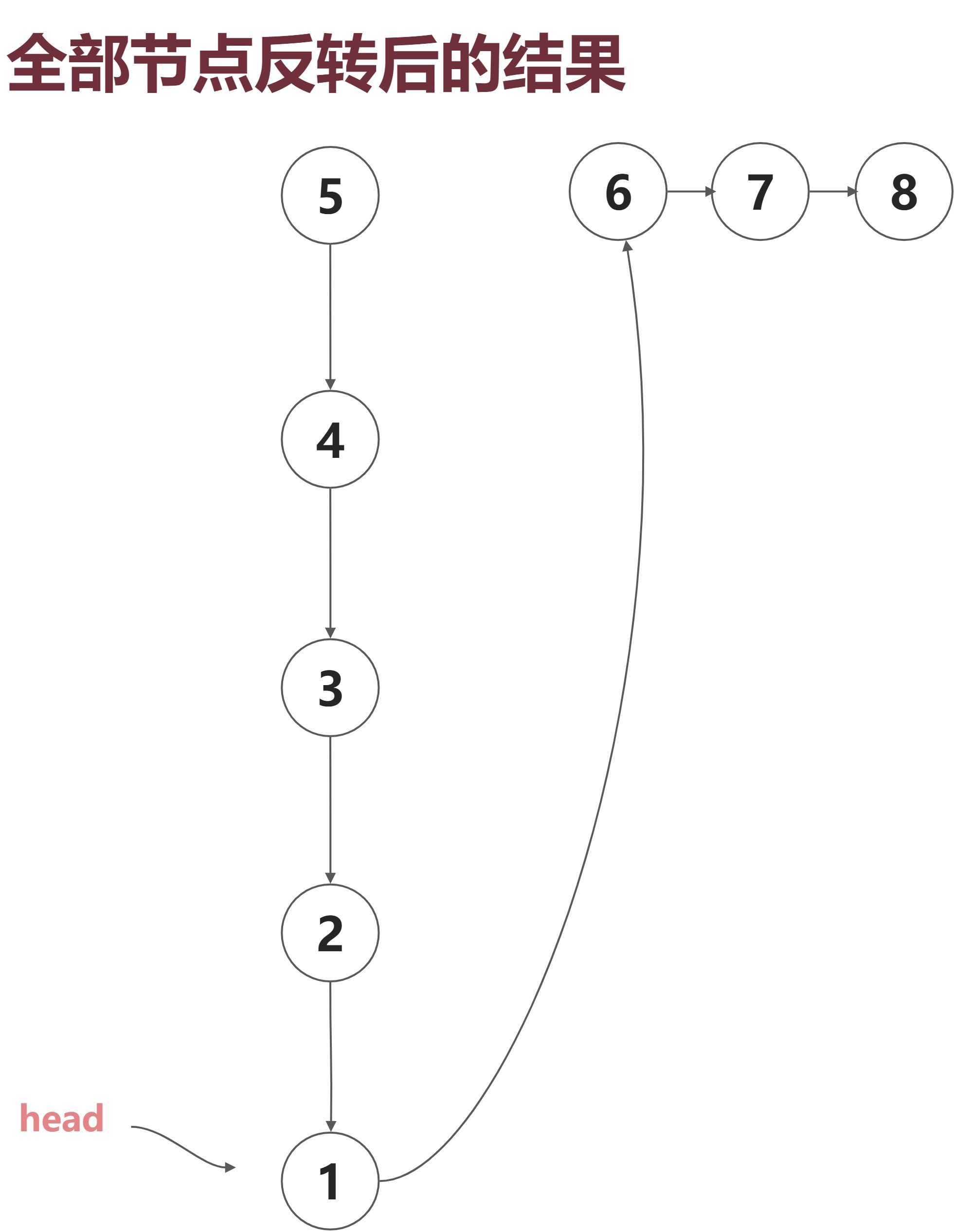
图解（head为1，n为5）

算法 - 图1
算法 - 图2
算法 - 图3
算法 - 图4

动态规划（Dynamic Programming）

什么时候需要用到动态规划？

问题中存在 ‘重叠子问题’

动态规划的要点/解题过程

  1. 找出【base case】
  2. 明确每一步的【状态】
  3. 明确每一步的【选择】
  4. 定义DP的含义
  1. int coinChange(int[] coins, int amount) {
  2.     // 题目要求的最终结果是 dp(amount)
  3.     return dp(coins, amount)
  4. }
  6. int dp(int[] coins, int amount) {
  7.     // base case
  8.     if (amount == 0) return 0;
  9.     if (amount < 0) return -1;
  11.     int res = Integer.MAX_VALUE;
  12.     for (int coin : coins) {
  13.         // 计算子问题的结果
  14.         int subProblem = dp(coins, amount - coin);
  15.         // 子问题无解则跳过
  16.         if (subProblem == -1) continue;
  17.         // 在子问题中选择最优解，然后加一
  18.         res = Math.min(res, subProblem + 1);
  19.     }
  21.     return res == Integer.MAX_VALUE ? -1 : res;
  22. }