概念：

1. 递归定义

- 递归函数

  • 对于某一函数f(x)，其定义域是集合A，那么若对于A集合中的某一个值x**0，其函数值 f(x0) 由 f(f(x0)) 决定，那么就称 f(x) **为递归函数。

    - 递归函数与表达式

  • 设 Y = f(x**0**)，F为由 f(Y) (Y∈A) 组成的任意表达式构成的递归表达式，则有 f(x) = F，并称 f(x) = F为递归函数表达式；称 Y 为递归自变量。

  • 例：
    • 递归函数表达式：

f(x) = f(x - 1) * f(x - 2)

  • 递归表达式 F：

f(x - 1) * f(x - 2)

  • 递归自变量 Y：

x - 1；x - 2

代码呈现

  • 如下代码所示即为针对f(x) = f(x - 1)递归函数表达式的代码呈现。其中：

    • f(x - 1) 为递归表达式F
    • x - 1 为递归自变量Y
      1. void F(int x)
      2. {
      3. F(x - 1);
      4. }

      - 递归出口

  • 对于给定的递归函数表达式 f(x) = F ，若存在x**0 [x0 **∈ A 且 x**0** = N (N为某一确定值)]使得该递归函数能够有限结束，则称表达式 x0 = N 为递归函数的出口条件表达式，简称出口条件。

  • 通过出口条件表达式组成的逻辑语句称为递归出口。

    代码呈现：

  • 如下代码所示即为针对包含了递归出口的f(x) = f(x - 1)递归函数表达式的代码呈现。其中：

    • if(x == 0) return; 为递归出口
    • x == 0 为出口条件
      1. void F(int x)
      2. {
      3. if(x == 0) return;
      4. F(x - 1);
      5. }

      2. 递归的组成部分及其作用

  • 对于递归，我们首先要清楚递归组成部分以及其作用。

  • 递归由以下四个部分组成，每个部分有相应的作用。

    - 遍历

    1. - 最重要的组成部分，其余组成部分都建立在**遍历**之上。
    2. - 它由**递归函数表达式 f(x) = F **决定，本身不做任何返回，仅通过递归自变量Y的不断改变以进行遍历。如：遍历链表 f(x) = f(x.next)

    - 求值

    1. - 与递归本身无关，它仅在递归遍历过程中的某一特定时刻下产生，是递归遍历过程中的产物。如：获取链表的最后一个节点。

    - 操作

    1. - 在遍历的过程中进行若干操作，以使递归函数富有意义。如：遍历链表时输出链表节点值。

    - 返回

    1. - 仅指递归结束后最终返回的内容。可以返回某个具体的值，也可单纯return，不返回任何内容。

注意：求值与返回是不同的任务。前者是通过递归获取某一时刻的值，但不代表其必须返回；后者强调递归结束调用后最终返回的结果。

3. 递归路径

- 定义

  • 递归路径是指在递归内部不断地调用自身时，依据递归自变量的不断改变，最终所呈现的一种调用轨迹。例如:
    • 递归函数表达式f(x) = f(x - 1)，其递归路径表现为一条递归自变量不断减小的线性路径。
    • 递归函数表达式f(x) = f(x - 1) * f(x - 2)，由于其递归表达式包含对递归函数的两次调用，所以它所呈现的是两条线性路径。

  • 综上，递归路径的数量由递归表达式所包含的递归函数的数量决定。

    - 主路径与分岔路径

  • 对于单条递归路径而言，该条路径即为递归函数遍历的主路径。

  • 对于多条递归路径而言，第一条也就是最先调用的路径为递归函数遍历的主路径。其余路径都称为分叉路径。

    - 递归路径的方向

  • 对于单条递归路径而言，其方向永远是固定不变的。

  • 对于多条路径，路径方向的改变受递归出口以及路径变换条件所决定。
    • 如果在一个递归函数内部没有递归出口以及路径变换条件能够结束递归的调用，那么该递归函数将无止境地遍历主路径，忽略分岔路径。
    • 如果拥有递归出口或路径变换条件，那么只有在其条件成立时，正在遍历的递归路径才会返回，从而执行下一条路径，即“变换了路径方向”。

  • 需要注意的是，递归路径方向的变换是一个及其短暂的过程。当结束了前一个递归路径的遍历后，下一条路径的遍历只会执行一次。换句话说，递归路径的方向在条件成立后只会改变一次，改变完以后又将回到主路径当中。

    4. “递”与“归”的整体路径表达

  • 前面我们了解了递归路径的相关知识，下面，我们就需要针对递归的整体路径表达进行一个深入的认识。

    - 递归的方向

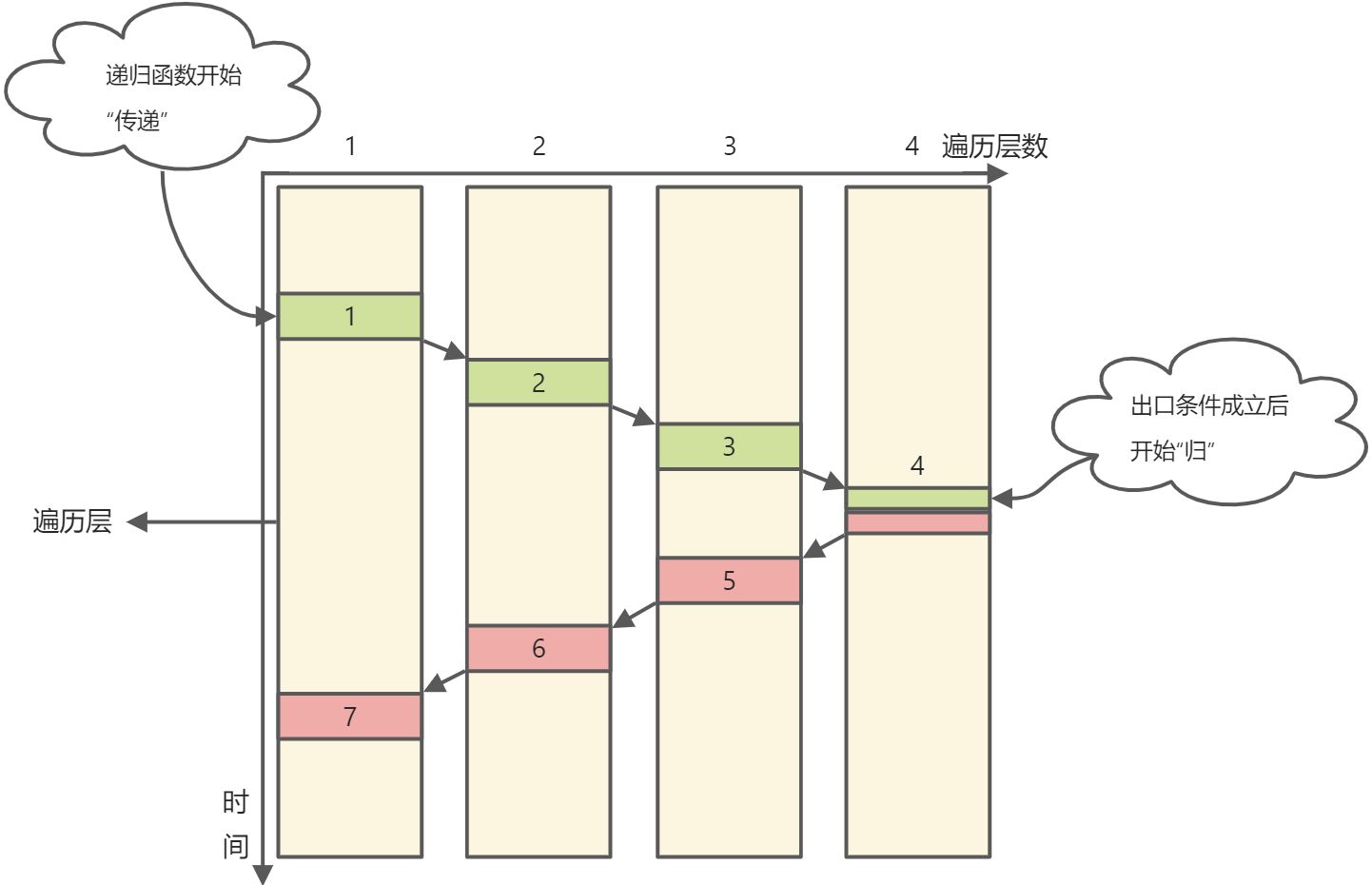
  • 以最简单的包含一条主路径的递归函数为例，递归的方向呈现一个“>”字形：

    • 横轴代表遍历层数，每一个黄色矩形代表一个遍历层。
    • 纵轴为遍历的时间消耗。
    • 图中的数字代表递归的调用顺序。
    • 绿色部分代表“递”的过程，方向为“1”->“2”->“3”->“4”。
    • 红色部分代表“归”的过程，方向为“4”->“3”->“2”->“1”。

递归基础 - 图1

- “递”与“归”的代码执行周期

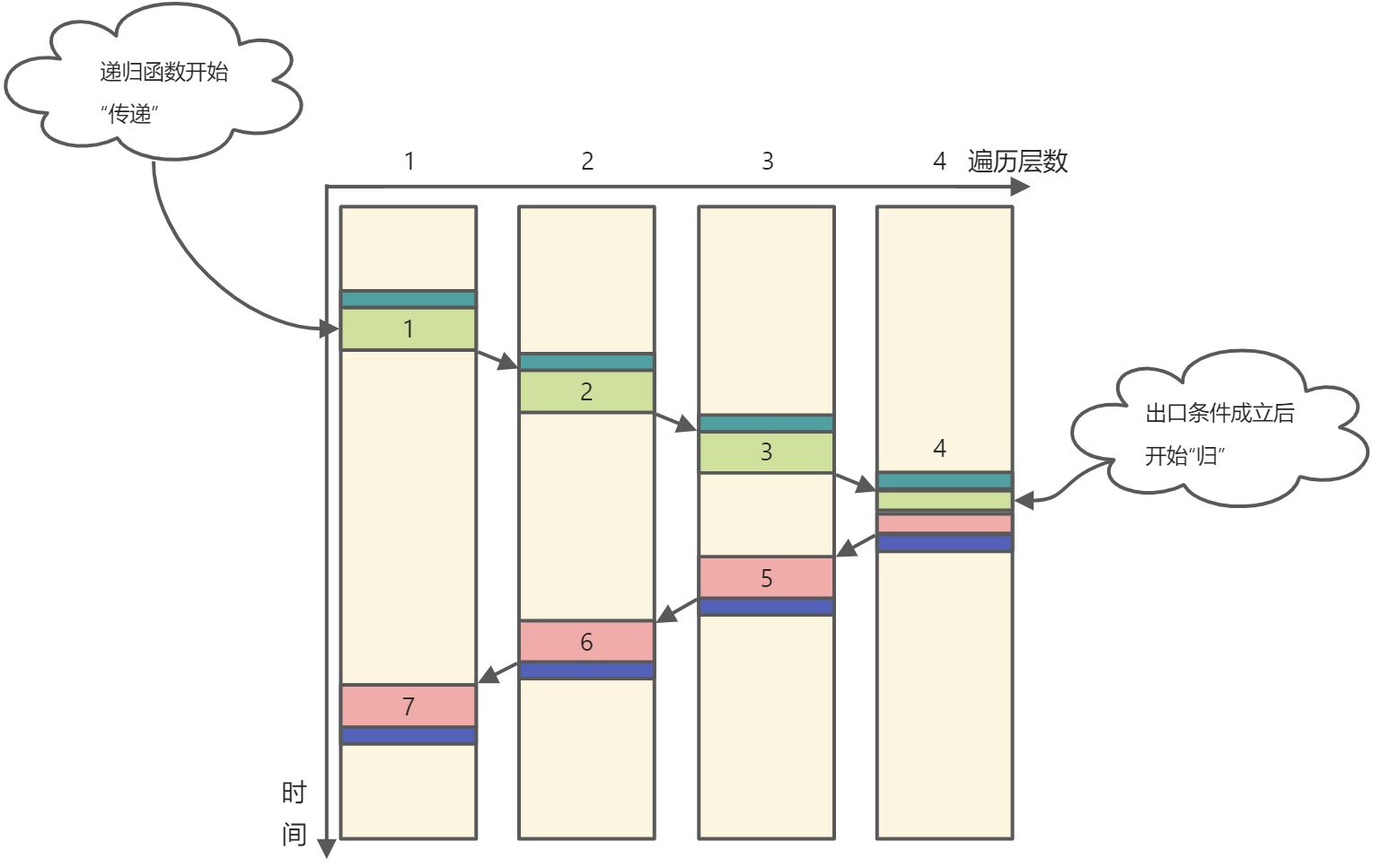
  • 在某一递归函数开始第一次调用其自身时，首先开启“递”过程，直到递归出口条件成立后，开启“归”过程。换句话说，“递”过程的开始取决于第一次对自己的调用，“归”过程的开始取决于递归出口的执行。

  • 从递归函数调用自身的这一时刻出发，我们可以将位于这一时刻之前与之后的两个时期分别称为“递”过程的代码执行周期与“归”过程的代码执行周期。

    “递”过程的代码执行周期

    • 发生在每一次“递”之前。当我们把一些代码操作放在递归调用代码的前面时，意味着这些代码将在每一次遍历之前执行，然后才开始进入下一次遍历。

    • 一般的，我们都将递归出口放置于递归调用代码之前，以便在每次遍历的时候先判断出口条件是否满足。

      “归”过程的代码执行周期

    • 发生在每一次“归”之后。当我们把一些代码操作放在递归调用代码的后面时，意味着这些代码只会在每一次遍历的返回之后执行，然后再次返回上一层遍历。

    • 一般的，我们习惯把一些需要先通过“递”过程才能完成的操作放置于递归调用代码之后。
  • 如下图所示，深绿色的色块代表“递”过程的代码执行周期，深蓝色的色块代表“归”过程的代码执行周期。

递归基础 - 图2

  • 在代码中可简单概况如下：
    1. void F(int x)
    2. {
    3.   //“递”过程的代码执行周期
    4.   ...
    5.   //- End -
    6.   F(x);                        //递归调用代码
    7.   //“归”过程的代码执行周期
    8.   ...
    9.   //- End -
    10. }

    组成部分详解

    1. 遍历

    在这一组成部分里，我们只需关注其遍历层面，而无需关心其余3个组成部分（求值、操作、返回）。

- 使用场景

  • 简单遍历一组数据或数据结构；

  • 找出位于该组数据或数据结构末尾的项。

    • 只需设定一个递归出口即可。一旦递归出口的出口条件被满足，就说明当前遍历层是整个递归遍历的最后一个遍历层。

      - 代码呈现

      （1）递归函数表达式

  • 在这一节中，我们需要将给定的递归函数表达式通过代码的形式展现出来：

    例1：f(x) = f(x - 1)

    • 该递归函数表达式呈现为一种递归自变量为数值型的遍历规则。我们只需将等号左边的部分定义成方法名与参数，将右边的部分（即递归表达式 F）呈现在方法体中进行调用即可：

      1. void f(int x)
      2. {
      3. f(x - 1);
      4. }

    • 按照上面的写法，可以看出这是一个无限遍历的递归函数。如果我们需要在某一条件成立后结束“递”的过程，只需在“递”过程的代码执行周期中添加递归出口即可：

      1. void F(int x)
      2. {
      3. if(x < 0) return;
      4. F(x - 1);
      5. }

    • 按照上面的写法，很容易可以看出当传入的x小于0时，直接结束整个递归 或 结束“递”过程，开启“归”过程，直至“归”过程结束以结束整个递归。

      例2：f(node) = f(node.next)

    • 这是一个标准的遍历链表的递归函数表达式，它呈现为一种递归自变量为结构型的遍历规则。

    • 可以发现，这里的递归自变量与上一个例子的递归自变量在本质上都是相同的，它们都能够通过对传入参数的进行相应的改变从而进行线性遍历。
    • 当当前节点node为空时，结束“递”过程，开启“归”过程，直至“归”过程结束以结束整个递归。
      1. void F(LinkedList node)
      2. {
      3. if(node == null) return;
      4. F(node.next);
      5. }

      （2）递归自变量

  • 在上一节中，我们通过两个例子展示了如何将给定的递归函数表达式转变成代码的方法。而在这一节中，我们将探寻其递归自变量的更多可能。

    例1：f(arr) = f(arr) {arr.RemoveAt(0);}
    • 在这个递归函数表达式里，“{}”括号内的代码是在“递”过程的代码执行周期中对递归自变量进行的一些改变操作。
    • 具体来说，arr参数是一个有若干数据的集合/数组，我们在“递”过程的代码执行周期中对arr进行了删除首元素的操作，后面再将arr传入，调用自身。

    • 那么为什么要这样表示呢？这是因为我们有时在编写代码的过程中，无法直接将一系列对递归自变量的改变操作写在递归表达式的括号“()”内，因此，我们就可以将它们分开来写。

      • 在C#语言中，针对List集合的删除某一索引位置的元素操作RemoveAt方法的返回值为void，即没有返回值，所以我们无法直接在括号“()”内表达。 ```csharp void F(List arr) { if(arr == null || arr.Count = 0) return;

      arr.RemoveAt(0); F(arr); } ```

    • 不难分析，上述代码的第5、6行代码都是对本例递归表达式F进行代码呈现的部分，通过对递归自变量的分开表达以对其进行改变，所以，在调用自身时传入的arr参数实际上与方法定义时传入的arr参数并不一样。

    • 另外，我们设定了一个递归出口，当传入的arr为空或arr集合没有任何数据时返回。
  • 总结：
    • 本质上来说，对于能够通过简短的一行代码对递归自变量进行某种改变并返回的情况，可以直接将递归自变量写在括号“()”内；
    • 对于需要对递归自变量进行复杂改变，或无法通过一行代码表示的情况，可以将修改操作的代码分开写在“递”过程的代码执行周期中。

      对于前面递归函数表达式为f(x) = f(x - 1)和f(node) = f(node.next)的例子，我们当然可以将递归自变量也分开写在上面，如： x = x - 1; node = node.next; F(x); F(node);

2. 求值

在这一节中，我们仅仅考虑在递归遍历过程中的求值问题，即思考这个值是什么、从哪里产生。至于这个值最后会去往哪里、返回到谁身上，则在最后一个组成部分——“返回”当中讲解。

- 使用场景

  • 在遍历的某一过程中生成某个所需要的值；

    - 代码呈现

    （1）生成P节点

  • 我们将以链表节点生成这一功能为例。

  • 在递归遍历的过程中，我们需要在每一个遍历层当中生成一个链表的节点，只需按如下代码写即可：

    • 对于遍历，我们可以简单地传入一个int型的集合List作为遍历参数，递归出口为当该集合为空或其元素个数为0时return。

    • 对于求值，我们需要在每一次“递”过程的代码执行周期中生成一个链表节点。

      1. void F(Lits<int> arr)
      2. {
      3. if(arr == null || arr.Count == 0) return;
      5. var p = new LinkedList
      6. {  
      7.    Data = arr[0],
      8.    Next = null
      9. };
      11. arr.RmeoveAt(0);
      12. F(arr)
      13. }

  • 在上面的代码中，我们让arr参数在每一个遍历层中都执行删除首元素操作以此进行对arr集合的遍历。然后在遍历的过程中，我们不断地生成一个节点P，并赋予其Data成员相应的值，Next成员指向null。如此，我们便解决了递归当中的一个简单的求值问题。

  • 值得注意的是，这个P值仅仅在每一个遍历层中被产生了，但它不会作用到任何地方去。如果想要最终返回这些节点，那么我们应该关注后续要讲的递归的返回问题。

3. 操作

在本节中，我们将思考在递归遍历过程中的操作问题。 操作，顾名思义就是一系列按照预期结果所实行的做法。

- 使用场景

  • 大部分使用递归的算法中都涉及到操作问题。如遍历一组数据时将其打印在屏幕上、反转链表时的反转操作等等。

- 代码呈现

（1）遍历链表并输出

  • 这是最简单的操作问题，只需在“递”过程的代码执行周期中进行对链表值的输出操作即可：

    1. void Print(LinkedList node)
    2. {
    3.   if(node == null) return;
    4.   //- 操作 -
    5.   Cnosole.WriteLnie(node.Data + " ");
    6.   //- End -
    7.   Print(node.Next);
    8. }

  • 如果要对链表进行反向输出，只需在“归”过程的代码执行周期中操作即可：

    1. void Print(LinkedList node)
    2. {
    3.   if(node == null) return;
    5.   Print(node.Next);
    6.   //- 操作 -
    7.   Cnosole.WriteLnie(node.Data + " ");
    8.   //- End -
    9. }

4. 返回

与“求值”问题不同，“返回”主要研究递归方法体里面的所有return问题。

- 使用场景

  • 每一个递归算法必包含若干return代码，至于返回的是什么则需要另行分析。

- 代码呈现

（1）Void

  • 无返回值：

    1. void F(int x)
    2. {
    3.   if (x < 0) return;
    5.   F(x - 1);
    6.   return;
    7. }

  • 上面的代码是一个非常简单的无返回值的递归，但与其说它没有返回值，不如说它屡次返回的都是void。

  • 另外，我们很容易能够发现，第6行的return代码是可以省略的，加上只是为了更好地演示其在“返回”问题中的作用。

（2）最终返回具体的值

  • “最终返回具体的值”是指这个递归方法被外部调用时最终返回的值。如果我们只考虑这个问题的话，则代码如下：

    1. int F(int x)
    2. {
    3.   if (x < 0) return 0;
    4.   F(x - 1);
    6.   return x;
    7. }

  • 其中，我们可以直接将第6行的return值视为整个递归方法最终返回给外部调用者的值。

（3）返回具体的值到上一个遍历层

  • 这里与例（2）不同的地方在于，我们还需要考虑前后遍历层的返回值问题。例（2）由于return以后，其递归方法体内部并没有任何地方接受下一个遍历层返回而来的值，所以它将只考虑最终返回给外部调用者返回值的问题。

  • 在这一例中，则需要考虑内部关系。代码如下：

    1. int F(int x)
    2. {
    3.   if (x < 0) return 0;
    4.   var p = F(x - 1);
    6.   return p;
    7. }

  • 在上述代码的第4行代码中，我们定义了一个变量p用来接收下一个遍历层返回的值，并且我们可以很容易地想到这个值是由下一个遍历层的第6行代码返回的。

PS：这第4个组成部分——“返回”或许在大家看来好像太过于简单，不需要将它独立出来作为一大组成部分。而此前笔者也的确尝试过直接把“求值”与“返回”问题结合起来讲解，但最终发现，求值与返回确实有相互独立的情况，即使return无处不在（返回void）。为了让读者能够更加清晰地写出想要的代码，遂还是决定分开讲解。

- 本篇完 -