实验数据统计分析（Statistics for Analysis of Experimental Data）

作者：Catherine A. Peters 翻译：CycleUser

原作者单位：普林斯顿大学 土木及环境工程学系(Department of Civil and Environmental Engineering，Princeton University，Princeton, NJ 08544) 原文链接

统计学，是对数据进行定量分析的一种工具，用于从数据中抽取（extract）有用的信息。在本章我们要面对的是通过实验获得的原始数据。实验可以对某一个研究对象进行多次的测试，也就是重复测试（replicate measurements），这样就肯定会有误差（error）。统计分析（Statistical analysis）就可以对这些观测结果进行总结，估计其平均状态（average），作为对真实平均值（true mean）的一个估计。除此以外，统计分析（Statistical analysis）的另一个作用是对数值的变化（variance）进行估计，作为对变量不确定性（uncertainty）的衡量。有时候我们对某个变量 a 进行测试，而可以用这个变量去推导另一个变量 b，我们可以把对变量 a 进行的测量运用到对 b 的分析上。统计分析可以用于估计出这种推导得到的变量的误差，这种误差通过数学模型而传递。有时候我们可能会测量两种不同变量，然后想要知道这两组不同的测量值之间是否有区别。这时候，就可以使用方差分析（analysis of variance，t 检验 (t-tests)），来推测现象背后是否有真正的区别。最后，还有一种情况，就是测量一个变量 x 以及另外一个随之而发生变化的变量 y。这时候就可以使用回归分析（regression analysis）来得到这两个变量之间的数学关系表达式。上面这些内容就是统计学在实验数据分析方面的一些具体的应用。本章将以环境工程领域中的典型实验测量为背景，来简要介绍这些应用。

本章内容相当简短。想要对相关理论进行深入学习的学生，建议去专门学习关于实验数据统计分析的教材。本章末尾的参考文献列表中有一些比较有用的教科书，其中的一些就直接是面向环境工程师和学者的。

误差分析和误差传递（Error Analysis and Error Propagation）

测量值的误差以及统计示范（Errors in Measured Quantities and Sample Statistics）

在我们设计实验和收集实验数据的时候，一定要时刻铭记，我们观察真实世界的能力是不完美的。我们的观察永远不可能完全地如我们预想的那样准确。这一情况可以用下面的数学公示表述：

测量值 = 真实值 ± 误差 （1）

误差来源包括了观测对象所固有的内部的不稳定性，也包括了能够影响观测的无数种因素。凡是能降低系统误差的方法，都可以用上，比如对实验仪器进行校正。完全去除所有的测试误差是不可能的。如果隐藏的误差真正的是随机值（random）而不是偏差（biased），那我们也可以进行多次观测来得到有用的信息，进行重复的对比观测（replicates），然后计算平均值。为了让取样（sample）能真正代表现象背后的本质，就一定要用随机取样（random sample）。例如，假设你在运行一个实验，其中有八个批量反应器（batch reactors），然后你就计划每个小时就牺牲掉其中的一个反应器来测试某个化学物质的浓度。每次你就要从省下的反应器中随机抽选一个。一定不能按照最开始准备的顺序来取样，也不能按照这些反应器在工作台上所排列的顺序来取样。你永远不能知道其他能影响反应器中控制过程的因素。通过随机取样，任何由于其他因素引起的系统误差，就都被随机分布于你的测试之中了。随机可以帮你确保观察的独立性（independence）。我们这里说的“独立观测（independent observations）”，本质意义是我们希望观测过程中的误差彼此独立。除了非随机取样之外，实验室里还有一些其他行为也会破坏观测的独立性。例如，如果一个没有经验的实验员比较熟练于做某个实验了，误差可能就会随着时间推移而降低。这种情况下，误差就和实验进行的次序有关了，这样先后的误差都不再是独立的了。与此类似，如果一个实验设备每次使用的时候都有损耗，那么随着时间推移，这个设备参与的实验误差就可能会增长。这样也产生了不独立的误差。随机取样以及其他能使观测误差相互独立的措施，都有助于保证实验的代表性（representativeness）。如果酥油的窜Ce 都是对同一个研究现象的有代表性的观测，那就都会有同样的均值和方差，也就意味着误差将是同分布的（identically distributed）。这里引入一个缩写 IID（independent identically distributed，独立同分布），指代的就是一个样本的观察是独立（independent）且遵循同分布（identically distributed）。

给定一个 n 次观察的样本，取样均值（sample average）的计算公式为：

$\bar x = \frac{\sum^n_{i=1}x_i}{n}$s (2)

上面式子中的$x_i$代表的是第 i 次独立观测。取样均值（sample average） 是一个统计量（statistic），是对均值（mean）$\eta$ 的一个估计，这个$\eta$也是中心趋势（central tendency），是潜在随机变量（underlying random variable）。样本方差（sample variance）的计算公式为：

$s^2 = \frac{\sum^n_{i=1}{(x_i-\bar x)^2}}{n1}$s (3)

样本方差（sample variance）也是一个统计量（statistic），是对于方差（variance）$\sigma ^2$的估计，这个$\sigma ^2$也是一个潜在随机变量。另外一个有用的变量是样本标准差（sample standard deviation）s，也就是样本方差的平方根，这个是对$\sigma$的估计。上面公式3中的分母 n-1 是与样本标准差相关的自由度数（number of degrees of freedom）。

通常情况，我们感兴趣的都是去估计平均值，而非单次的观测。我们真正想要了解的是平均值的变化情况。也就是说，x 的扰动是如何转换成我们估计平均值时候的不确定性的？均值的标准误差（standard error of the mean） 的计算公式为： $s_{\bar x}=\frac{s}{\sqrt n}$（4）

这个均值标准误差，也是有 n-1的自由度。很明显，当观察次数 n 非常大的时候，那么我们对均值估计的不确定性就降低了。这个关系就表明，进行单次观测的不确定性远大于多次观测取平均值得到的估计值。即便研究对象本身就有很大的扰动，并且还有很多非常显著的测试误差，进行多次观测依然可以降低对均值估计的不确定性。

样例

一个学生从一个井中收集了十二份地下水样本。她先测量了其中六份的溶解氧。得到的测量值（单位 mg/L）分别为： 8.8，3.1，4.2，6.2，7.6，3.6 取样平均值为 5.6 mg/L，样本标准差为 2.3 mg/L。这个值可以解释为对这几份样品溶解氧浓度测量的误差（error）或者不确定度（uncertainty）。要注意这里数据的波动情况，既包含水井中水的溶解氧本身的波动特征，也包含了实验误差。均值的标准误差（standard error）是 0.95 mg/L。要注意这个值就比样本标准差小很多了。这个学生进行了上述统计之后，认为均值估计的不确定度太大了，无法接受。然后她继续测量剩下的六个水样本中的溶解氧浓度。得到的观测值（单位 mg/L）为： 5.2，8.6，6.3，1.8，6.8，3.9

全部的十二个测量值的平均值是 5.5 mg/L，样本标准差是 2.2 mg/L。用全部十二个样本的统计数据进行对比，可以发现最开始的留个样本也具有一定代表性，可以反映现象背后的本质规律。新得到的均值的标准误差（standard error）是 0.65 mg/L。这表明不确定度降低了，应该是由于有了更大规模的样本来进行测量。

正态分布（Normal Distribution）

在实验中，有一种常见情况，就是要计算的样品平均值和样本标准误差，来推测观测背后的随机变量的概率特征，或者推测与其他随机变量的关系。要进行这种推测，就需要对实验检测中误差的概率分布的形态预设一个假设。大多数的统计方法做出的假设都是测试误差符合正态分布（normal probability distribution）。正态分布也称为高斯分布（Gaussian Distribution）。图1a 即一个正态分布的概率分布函数（probability distribution function，缩写为 PDF）图形，其中的随机变量为 x，均值$\sigma$为0，单位标准偏差（standard deviation of unity），即$\eta$ 为1。对于一个给定的 x 的值，在 y 方向上的值就是函数 f(x)，即概率密度。正态分布的概率密度函数是对称的（symmetric），其中心位置就在 x 的均值位置，这个函数覆盖了从负无穷到正无穷的范围。通过定义可知，概率密度函数下覆盖的面积总和应该是单位1。对于一个正态分布的概率密度分布函数来说，有 68% 的区域在$\eta\pm\delta$范围内，这就意味着测量值有68%的概率落在距离均值一个标准偏差的范围内。在实践中，就是实验者可以预计大约有2/3的样本的观测结果会在这个范围内。$\eta\pm 2\delta$的范围覆盖了曲线下 95%的范围，而$\eta\pm 3\delta$则覆盖了整个概率的 99.7%。对正态分布进行观察的另一个手段就是使用累积分布函数（cumulative distribution function，缩写为 CDF），如图1b 所示。对于一个给定的 x 值，y 轴方向的函数值 F(x)是随机变量小于等于 x 的累积概率。 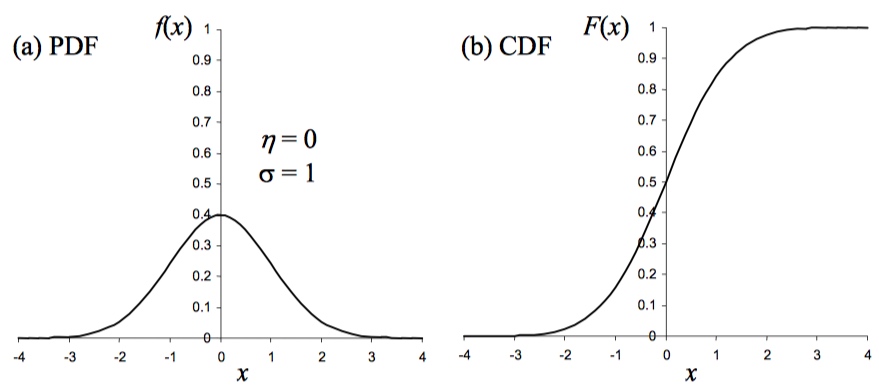图1-a 图1-b 上图中，a 是概率分布函数图，b 是累积分布函数图，随机变量为 x，均值$\eta$为0，$\sigma$为单位标准偏差。

注意，在很多统计方法的应用中，都有一个规定，就是观测的误差是正态分布的，而并非随机变量本身是正态分布的。这是很重要的区别，因为很多环境变量本身有自己的分布函数，而不遵循正态分布。例如，有的随机变量就不能假设有负值，比如浓度；另外，有的随机变量会有非常大的数量及变化，例如多孔介质中的渗透系数就通常是对数分布（lognormally distributed）的，也就是随机变量的对数函数（logarithm）符合正态分布。此外，还有一种正偏（positively skewed）概率分布函数，γ分布（gamma distribution）广泛用于降水量之类的环境变量。

如果针对某个观测对象进行了无穷多次的重复试验，那就可能检验这些观测的误差是否符合正态分布。可以借助正态分布图解（normal probability plot）来实现。正态概率图是正态累积分布函数（CDF）的一种形式，其中对 y 轴进行了调整，以使累积分布函数呈现线性。实验者可以对观测结果构建一个排序列表（rank-orderd list）估计累积概率，然后在正态概率纸上进行投图（更多内容参考 McBean and Rovers，1998）。

尽管有时候，随机变量可能会因为时间空间等的变化而成为非正态分布的，也还可以用正态分布去描述这些非正态分布的某些特征。如前文所述，误差内包含了随机变量本身的变化特征，也包含了测试误差。测试误差可能有很多诱因，比如实验设计、取样、探测和分析相关的很多小的因素。例如，温度计的厂家可能没有校正好，所以温度标度值和水印位置可能不完全匹配。温度计中的水银也可能不够纯净，所以不完全以可重现的方式进行热胀冷缩。实验者的视线在读数的时候有偏差。测得温度可能随着测试时间的推移而波动变化。温度还可能正好在实验者测试记录温度的空间位置上发生了变化。种种这些可能累加在一起，就构成了实验测试中的误差。中心极限定理（central limit theorem）说，随着变量总数的增加，不论这些随机变量本身的分布是什么形态的，随机变量之和的分布都会接近正态分布。实验观测的误差就是不同误差的综合产物。如果误差来源很多（通常如此），那么根据中心极限定理，我们就可以认为实验误差趋于正态分布。此外，我们通常使用统计工具来对样本均值进行推测，而这正是对这些值本身可能有正态分布误差的一个进一步的推论。者提供了额外的理由来假设样本均值具有正态分布的误差。

通常在实验中，我们可能未必有充分多的观测来获得正态概率图，也就不能根据覆盖的概率分布来进行判断。在上面测试水井中水的氧逸度的样例中，即便一共有12次观测，也不足以推断出正态概率图的线性特征。通常我们只进行两三次的重复测试，足够建立一个有意义的概率图就行了。在这些情况下，我们就必须预设正态分布误差结构了。好在有中心极限定理，作为理论基础，可以用来针对实验观测进行假设。

置信区间（Confidence Intervals）

对任意的一个估计的统计量来说，例如样本均值，我们要估计其本身的值，以及这个值的标准误差，这时候就可以给出置信区间（confidence intervals）。如果观测变量的误差 x 有一个正态概率分布，而所有观测之间彼此独立，那么样本均值误差的概率分布，由样本均值的标准误差来归一化，就是 t 分布（t-distribution）。t 分布是一个对称的概率分布，中间位置是 0，这和正态概率分布一样。而与正态概率分布不同的地方是 t 分布有变化幅度（variance），会随着目标统计量的标准误差的自由度的变化而变化。还记得上文中我们提到过的，$S_{\bar x}$有 n-1 的自由度。如果只进行了很少次数的观测，那么自由度数很小，t 分布的变化幅度（variance）就很大。

t 分布可以用于检测确定一个 t 值（t-statistic），用来计算出真实平均值$\eta$的置信区间。t 值确定了有 $n-1$ 自由度的 t 分布内所选择的概率范围，$1-\alpha$。例如，在 90% 的概率，即$1-\alpha =0.90$，$\alpha=0.10$。很多统计教材都会提供不同概率范围和不同自由度所对应的 t 值的表格，统计学方面的各种软件包也可以计算这个值。对$\eta$来说，$1-\alpha$ 置信区间为： $\bar x \pm t{n-1;\alpha/2}s{\bar x}$(5)

上式中，选用的是对应 $\alpha/2$ 的 t 值，因为 t 值用在±号后面，是对称的，所以单侧是 $\alpha/2$，加到一起就是$\alpha$了。这样就可以说置信区间包含$\eta$的真实值的概率为$1-\alpha$。通常用到的置信层次有90% (somewhat confident), 95% (fairly confident), and 99% (quite confident)。

样例

对于上面样例中的氧浓度数据，均值的95%置信区间是什么？均值标准误差的自由度为 12-1=11。在 t 分布中查找对应 11 自由度，置信概率 95%的 t 值为： $t_{11;0.025}=2.201$ 这样就有了95%的概率来确保氧浓度的真实值处于下列区间： $$ 5.5 \pm 2.201 \times 0.65 mg/L = 5.5 \pm 1.4 mg/L = 4.1 \pm 6.9 mg/L $$

这里要注意，通常需要包含在报告内的是标准误差，或者是用 t 值乘以标准误差的值，一般不超过两位有效数字。$t{n-1;\alpha/2}s{\bar x}$这个项目的大小表征了应该在样本均值的报告值中使用多少有效数字。在本样例中，也同样适用三维有效数字来记录样本均值的报告纸就可以了，也就是 5.51mg/L，因为这就表示了估计水平上的精确度。如果标准误差的值记录为 0.065mg/L，那么$t{n-1;\alpha/2}s{\bar x}$这个项目就应当记作 0.14mg/L。在这个案例中，用三位有效数字记录样本均值就足够了。

在本节界为之前，要考虑有时候报告的置信区间并不一定能真实地代表观测的不确定性，因为样本标准偏差（sample standard deviation）可能无法捕获到观测中所有变异的来源。要精确估计一个测试的不确定度，必须去进行重复实验（replicate measurements）。真正的重复需要对实验中能够引起误差的所有方面都设置冗余。例如，假如一个实验是通过测量随着时间变化的反应物浓度来推断反应速率。实验者可以设置一个单独的反应容器，然后在特定的时间点选取样本进行分析。要提高精度，实验者就可以在每个时间点选择多个样本，然后对测量的浓度取平均值。由于取样或者样品处理上的一些不一致，可能会存在一些变异，但所有的取样样品都来自同一个反应器。这样就还有很多潜在的误差来源没有被捕获，因为一直在从同一个反应器里进行重复取样。这个实验本身并不是重复的。更好的实验设计思路是设置多个反应器，然后理想的情况下就是在不同的时间段和不同的空间位置来进行实验。有时候时间和资源都构成了约束，让实验者没办法这样做。这样的话，数据分析人员就必须要认识到观测的样本的变化范围是比真实不确定度的范围扩展了的。

导出量的误差估计（Estimation of Errors in Derived Quantities）

有一种很常见的情况，我们进行实验观测之后，并不是直接使用这个数据，而是用来去推导一些难以直接观测的量值。例如，如果我们想要知道一种流体的密度，最简单的方法就是对一个定量体积的该流体进行称重。这样用重量除以体积，就能得出密度值了。那么问题来了，如何把重量和体积的测量误差转移成计算得到的密度的误差呢？

假设有一个额随机变量 z，是 N 个随机变量 {$x1,x_2,x_3,…,x_N$}的函数。很明显，如果我们假设误差比较小，而各个随机变量 {$x_1,x_2,x_3,…,x_N$}之间又没有协方差（covariance），那么就可以对 z 的误差进行泰勒级数展开（Taylor series expansion），得到了下面这个 z 的方差（variance）的表达式： $\sigma^2_z=\sum^N{i=1}{\frac{\partial z}{\partial xi}}^2{\sigma^2{x_i}}$(6)

如果已经估计了测量变量的样本方差(sample variances of the measured variables)，则可以使用上式中的关系来估计作为自变量函数的导出量的方差。

公式6还对独立变量的不确定性进行了划分，在此基础上，可以来判断哪些测试最重要，以提高导出量的估计精度。每个独立变量 $xi$ 都对导出量 z 的变化由两方面的贡献，首先是独立变量$x_i$ 本身的不确定性，也就是$\sigma{x_i}$，然后就是在 z 对 $x_i$ 的数学敏感度上，即偏微分部分$\frac{\partial z}{\partial x_i}$。

在讲更多内容之前，咱们先回顾一下实验数据的协方差（covariance）的概念。协方差为0，并不意味着 $x_1$和 $x_2$之间不具有相关性，而只是意味着这两者的变化是相互独立无关的。例如，我们知道材料的密度是与重量和体积相关的。对于某种材料来说，重量和体积是绝对彼此相关联的。体积更大的必然有更重的重量，反过来也是如此。然而，没有理由去认为测量重量的误差和测量体积的误差就有相关性。（译者注：即一坨铁的重量和体积是相关的，但是用天平称量重量和用量杯称量体积这两个过程中两者的误差往往可能是不相关的。）

举个例子，设某个导出量 z ，与其他的变量可加性相关（additively related），比如有两个随机变量$x1$和 $x_2$，而 z 是这两个随机变量的加权和（weighted sum）： $z= a x_1 +b x_2$(7) 上式中的 a 和 b 都是常数量。如果 $x_1$和 $x_2$之间协方差为0，那么 z 的方差为： $\sigma^2_z= a^2 \sigma^2{x1} +b^2\sigma^2{x_2}$(8)

把 z 写成一个求和的形式，就得到了 N 个独立变量的加权和的形式： $z= \sum^N_{i=1}a_ix_i$(9)

上式中的 $a_i$还是针对各个变量$x_i$的常数系数，那么 z 的方差为：

$\sigma^2z= \sum^N{i=1}a^2i \sigma^2{x_i}$(10)

样例

假设一个实验，目的是去估计在阳光下一个小平底锅中水的蒸发量。实验者称重得到了 4.0kg 的水，倒进了平底锅里面，然后再重复该过程 4 次，也就是一共加了 5 次，每次都是加 4.0kg 的水。一直没下雨，一段时间过后，称重，发现锅内剩余的水重量为 16.2kg。估计损失的水重量即蒸发作用导致，蒸发量 E 为与水的初始总量和剩余量相关的函数： $E= 5 A - R$ 上式中的 A 是每次加水的重量，R 是平底锅内剩余水的重量。经过上述实验过程，计算得到的 E 的值为 3.8kg。基于多次测试和过去的经验，实验者估计用来测量每次所加水量的设备的标准偏差（standard deviation）是 0.1kg，即 $S_A=0.1kg$。测量剩余水量用的是另外一个更大的量器，其测量误差为$S_R=0.2kg$。假设 A 和 R 的测量不具有协方差（covariance），那么 E 估计值的标准偏差为： $$ \begin{aligned} S_E&=\sqrt{5^2S^2_A +(-1)^2S^2_R}\ &=\sqrt{25(0.01)+0.04}\ &=\sqrt{0./25+0.04}\ &=0.54 kg\ \end{aligned} $$

很明显，导出量 E 的估计误差，要比参与计算的每个变量的误差大很多。

有的时候，导出量是通过测试量相乘得到的。例如一个随机变量 z，是两个随机变量$x_1$和 $x_2$的乘积，每一个都还有各自的指数： $z= x_1^a x_2^b$(11)

对上式进行微分，推导出 z 关于$x_1$和 $x_2$的偏导数，然后利用公式6，就可以推导出 z 的方差表达式。另外，我们也可以对公式11进行双侧取对数，得到下面的形式： $\ln z =a\ln x_1+b\ln x_2$（12）

假设$x1$和 $x_2$相互独立（也就是没有协方差），那么可以将公式10中的原则应用到上面这个式子，得到了： $\sigma^2{\ln z}=a^2\sigma^2{\ln x_1}+b^2\sigma^2{\ln x_2}$（13）

随机变量的自然对数的标准偏差近似等于相对标准误差（也称为变异系数），即： $sigma_{\ln z}\approx \frac{\sigma_x}{x} $（14）

如果这个变量的标准偏差很小，就可以近似相等。对于那些学过微积分的人，这个近似关系看上去应该很眼熟，对数函数的微分公式就是：

$d\ln z =\frac{dx}{x}$

只要相对标准误差小于 10%，即$\sigma_x/x\leq 0.10$，就可以应用公式14中的近似相等关系。甚至即便相对标准误差达到了 20%，也还可以用。将公式14中的近似相等关系应用到公式13中得到了公式15：

$\frac{\sigma^2_z}{z^2}=a^2\frac{\sigma^2_x}{x^2}+b^2\frac{\sigma^2_y}{y^2}$（15）

对于乘法关系来说，导出量的误差不仅依赖于自变量和数学敏感度，还依赖于自变量的大小。一般来说，对于一个变量 z，如果是 N 个自变量的乘积： $z=\prod^N_{i=1}x_i^{a_i}$(16)

z 的相对方差（relative variance）为：

$\frac{\sigma^2z}{z^2}=\sum^N{i=1}ai^2\frac{\sigma^2{x_i}}{x_i^2}$（17）

在对 x 进行了重复观测的情况下，通过对相对标准误差(relative standard error)$s{\bar x}/\bar x$进行估计得到变异系数（coefficient of variation）$\sigma{\bar x}/\bar x$。

样例

假设有一个实验，要推导液体密度 ρ，手段是分别测量质量 M 和体积 V。那么 M 和 V 的误差会怎样传递到导出的 ρ 上呢？ $$ \begin{aligned} \rho&=\frac MV \ \ln \rho &= \ln M+\ln V\ \sigma^2{\ln\rho }&=\sigma^2{\ln M}+\sigma^2_{\ln V}\ \end{aligned} $$

如果 M 和 V 的误差不是特别夸张地大，则： $$ \begin{aligned} \frac{\sigma^2{\rho}}{\rho^2}&=\frac{\sigma^2_M}{M^2}+\frac{\sigma^2_V}{V^2}\ \frac{\sigma{\rho}}{\rho }&=\sqrt{(\frac{\sigma_M}{M})^2+(\frac{\sigma_V}{V})^2}\ \end{aligned} $$

相对标准误差$\frac{S_M}{M}$是对$\frac{\sigma _M}{M}$和$\frac{\sigma _V}{V}$的估计。

假设 M 的相对标准误差是 0.01，也就是1%，V 的相对标准误差为 0.05，即5%。那么推导出的密度 ρ的相对标准误差如何计算呢？如下所示： $\frac{S_\rho }{\rho}=\sqrt{0.01^2+0.05^2}\approx 0.05$

如上式所示，推导量密度 ρ 的误差是 5%。在这个案例中，密度估计值的误差就主要受到了体积测量值的不确定性的控制。所以要提高密度的数据精度，最有效的方法就是提高体积测量的精度。

假设检验和 t 检验（Hypothesis Testing and the t-Test）

统计方法的另外一个常用用途是去对比一个测量值和已知值或者另外一个测量值。例如，假设某个实验，检测特定矿物在某成分溶液中的溶解速率。假设有两个感兴趣的条件。通常有两种方法来设计此实验。第一种思路是，在一个条件下建立多个重复的试验系统，在其他条件下再建立其他条件的冗余重复试验系统用于观测。假设上述不同条件系统所测试得到的溶解度就代表了对应条件下的溶解度。这种情况下，实验者关心的是对上述两种条件下得到的两个平均值的对比，以及对这两个值的差异程度进行推断。另一种方法是，一系列的试验系统都设定为同一条件，全部测量溶解度。然后在没给系统中改变溶液化学条件，再重新测量溶解度。这样每两个试验系统就明显不是互相独立的，也就不能分开来分析了。这种情况下，实验者会测试每个实验系统中的溶解度的变化量，然后计算溶解度差值的平均值。这个平均值可以跟一个已知的值来进行对比。显然，会存在一些技术上的限制使得某种特定的实验设计优于另一种设计思路，但这两种实验设计都能允许实验者去测试溶液化学条件对矿物溶解度上的影响。对实验人员来说，了解每种情况下数据分析所适用的统计程序是很重要的。

评估不同观测样本间差异的统计分析叫做变化幅度分析/方差分析（analysis of variance），缩写为ANOVA。这种分析通常要同时对多个不同设定的实验观察进行对比，而不是指对比两组的两个平均值。如果是值对比两个平均值，或者对比一个平均值和一个已知的值，就从ANOVA简化成了 t 检验。关于 ANOVA 以及与多重观察相关的实验设计，可以参考 Box, et al. (1978)。接下来将要讨论 t 检验的简单情况，对比两个值。在统计学t检验中，以及其他的统计测试中，第一步是要构建所谓的零假设（null hypothesis）。在对比两个值的情境中，传统的零假设就是声明要对比的这两个值没有差异。然后我们分析数据以检查相对于特定替代假设拒绝零假设的证据范围。