扩展欧几里得算法

在说扩展欧几里得算法之前，我们首先要为大家介绍的是欧几里得算法。欧几里得算法，又称为辗转相除法，是用来计算两个正整数的最大公约数(Greatest Common Divisor)的快速算法。欧几里得算法主要基于以下结论得出最大公约数。两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。用公式表达如下：
gcd(a,b)=gcd(b,a%b)
扩展欧几里得算法的作用是，已知整数a、b，在求得a,b最大公约数的同时，找到整数x，y (有一个可能为负数)，使之满足贝祖等式：
ax+by=gcd(a,b)
贝祖定理：若存在a、b是整数，则必存在整数x、y，满足ax+by=gcd(a,b)
换句话说，如果ax+by=m有解，那么m一定是gcd(a,b)的若干倍（可以来判断一个这样的式子有没有解）
有一个直接的应用就是 如果ax+by=1有解，那么gcd(a,b)=1

代码（求特解）

//扩展欧几里德
int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
/*
    y=y-a/b*x(第8行)推导过程
    gcd(a,b) = gcd(b,a % b)
     ax + by = by + (a % b)x
     ax + by = by + (a - a / b * b)x
     ax + by = by + ax - (a / b) * bx
     ax + by = ax + b(y - a / b * x)
                 y = y - a / b * x
*/

求通解

现在，我们已经通过 exgcd 求出了一组特解 x,y，记为 x0,y0 。
对于这一组特解，另一组解一定能写成 (x0+p),(y0+q) 的形式。其中 p,q 为任意整数。
那么就有
a(x0+p)+b(y0+q)=gcd(a,b)
∵ax0+by0=gcd(a,b)
∴a(x0+p)+b(y0+q)=ax0+by0
ax0+by0+ap+bq=ax0+by0
ap=−bq
解得：
p=−b/a q
∵ x,y 是整数，∴ p,q 也是整数。
进而得到 ap 一定是 b 的倍数。
将b/a化为 ( b/gcd(a,b) ) / ( a/gcd(a,b) )
此时有分子分母互质，因此，q 必须是 a/gcd(a,b) 的倍数。
同理得 p 必须是 b/gcd(a,b) 的倍数。
于是得到了通解：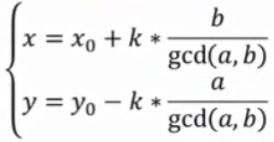

其中 k 为任意整数。 7: