任务：

  1. 40 数组中最小的K的数 . 这道题核心还是训练partition 的过程。

  2. 53 在排序数组中查找数字 考察 二分

  3. 57 和为s的数字 查找

  4. 61 扑克牌中的顺子。 杂题

  5. 62 圆圈中的最后剩下的数字。。约瑟夫环，比较经典的笔试题。

  6. 56 数组中数字出现的次数。。。用到了位运算知识，你先自己看看。

  7. 29 顺时针打印矩阵 二维数组遍历，找规律

40. 数组中最小的K的数

image.png

1. 思路

  • 库函数排序
    • 直接对arr排序，然后输出前k个
  • 大顶堆
    • 由于每次从堆顶弹出的数都是堆中最大的，最小的 k 个元素一定会留在堆里。
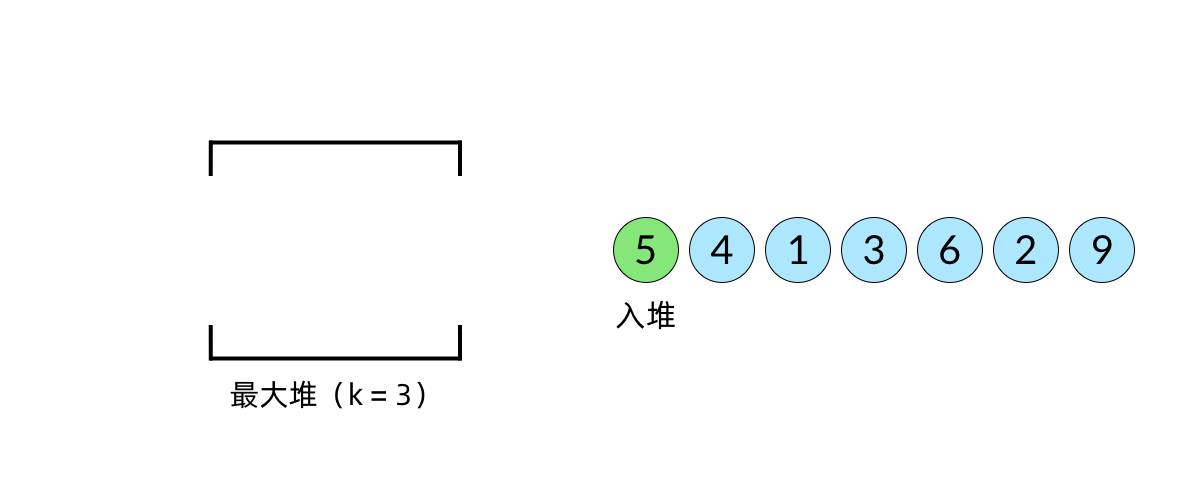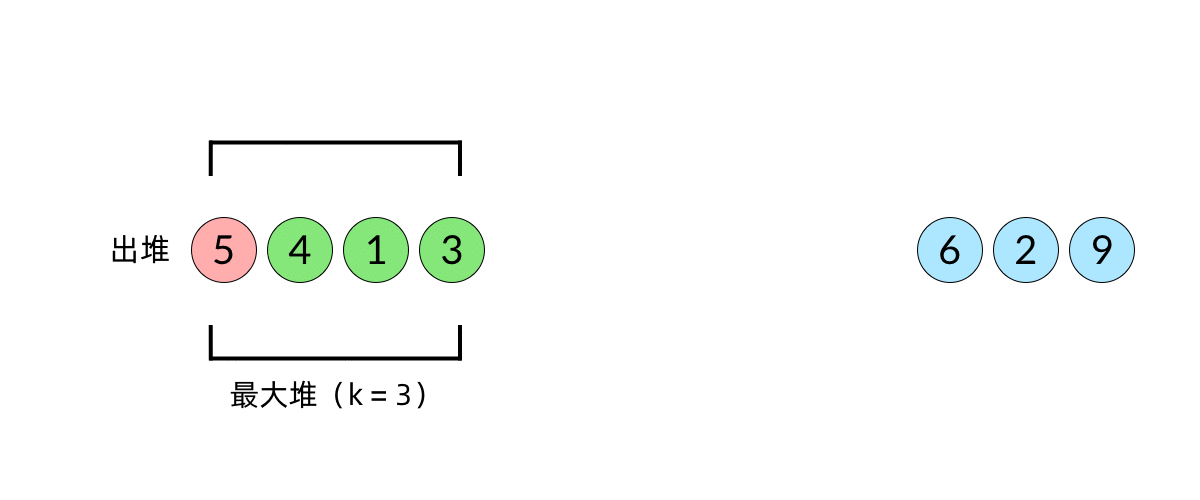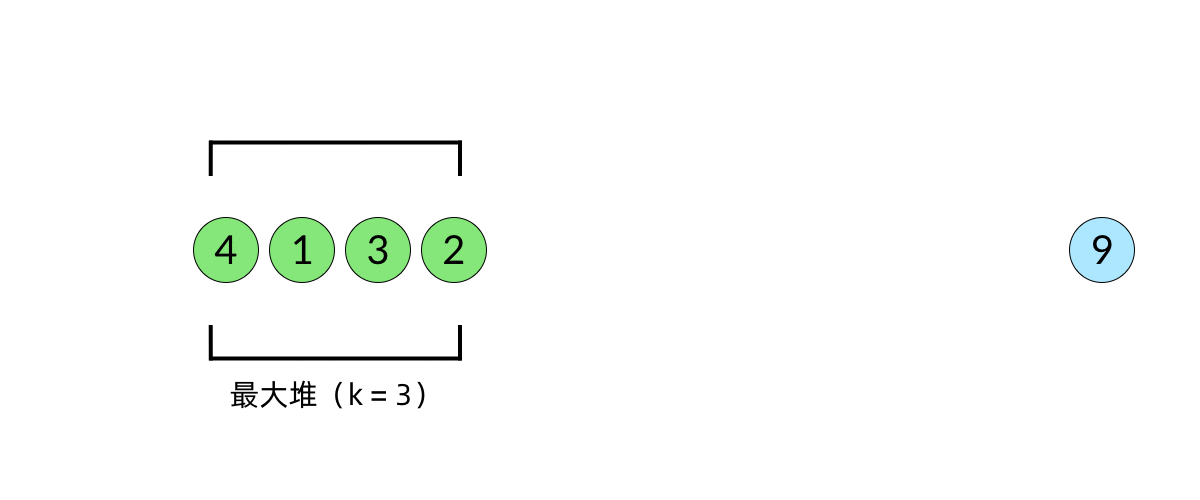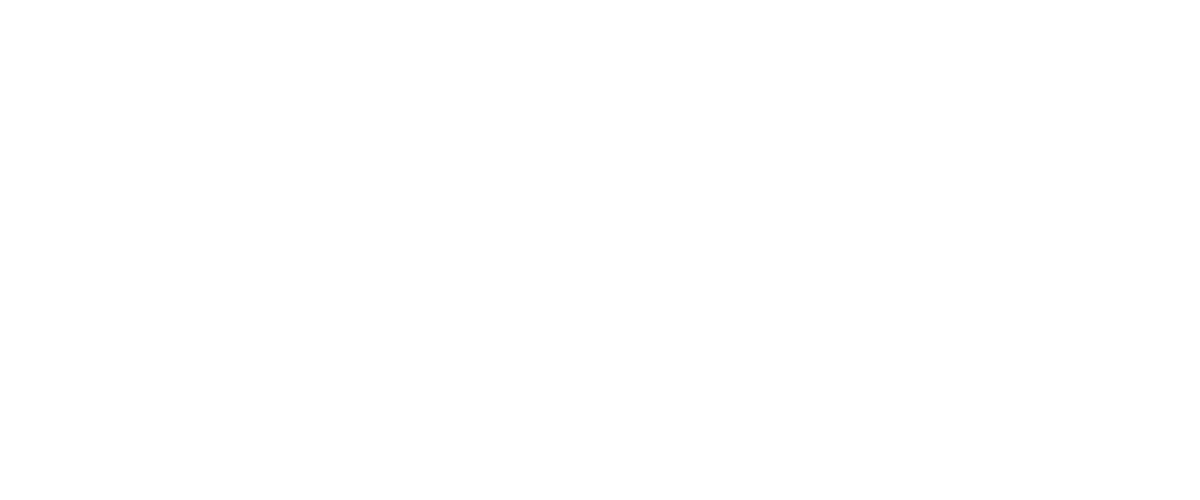
    • ffd837f564946747ff6fca9df7568fa894494f2e46fe0fe2d6590123432f0a57.gif

  • 快速排序

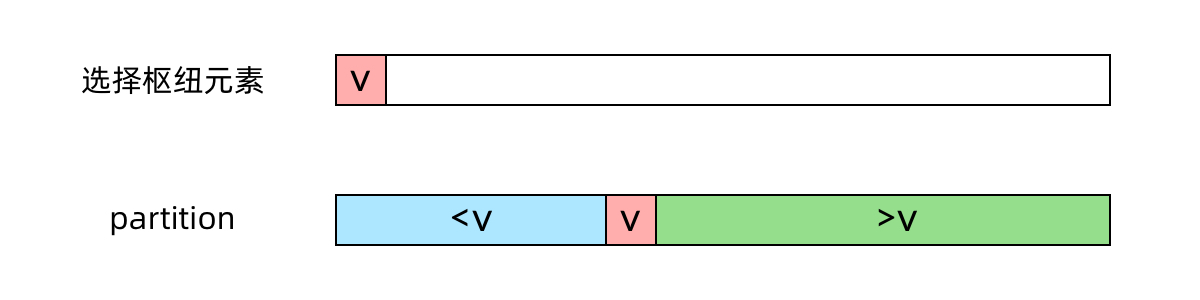
    • image.png
    • 随机选一个纽扣元素v
    • 把大于v的放右，把<v的放左
    • 左侧为m
    • 若 k = m，我们就找到了最小的 k 个数，就是左侧的数组；
    • 若 k<m ，则最小的 k 个数一定都在左侧数组中，我们只需要对左侧数组递归地 parition 即可；

    • 若 k>m，则左侧数组中的 m个数都属于最小的 kk 个数，我们还需要在右侧数组中寻找最小的 k-mk个数，对右侧数组递归地 partition 即可。

      2. 库函数排序

      1. class Solution:
      2. def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
      3.    arr.sort()
      4.    return arr[:k]

      3. 大顶堆

      1. class Solution:
      2. def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
      3.    if k == 0:
      4.        return list()
      6.    hp = [-x for x in arr[:k]]
      7.    heapq.heapify(hp)
      8.    for i in range(k, len(arr)):
      9.        if -hp[0] > arr[i]:
      10.            heapq.heappop(hp)
      11.            heapq.heappush(hp, -arr[i])
      12.    ans = [-x for x in hp]
      13.    return ans

      4. 快速选择

      1. class Solution:
      2. def partition(self, nums, l, r):
      3.    pivot = nums[r]
      4.    i = l - 1
      5.    for j in range(l, r):
      6.        if nums[j] <= pivot:
      7.            i += 1
      8.            nums[i], nums[j] = nums[j], nums[i]
      9.    nums[i + 1], nums[r] = nums[r], nums[i + 1]
      10.    return i + 1
      12. def randomized_partition(self, nums, l, r):
      13.    i = random.randint(l, r)
      14.    nums[r], nums[i] = nums[i], nums[r]
      15.    return self.partition(nums, l, r)
      17. def randomized_selected(self, arr, l, r, k):
      18.    pos = self.randomized_partition(arr, l, r)
      19.    num = pos - l + 1
      20.    if k < num:
      21.        self.randomized_selected(arr, l, pos - 1, k)
      22.    elif k > num:
      23.        self.randomized_selected(arr, pos + 1, r, k - num)
      25. def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
      26.    if k == 0:
      27.        return list()
      28.    self.randomized_selected(arr, 0, len(arr) - 1, k)
      29.    return arr[:k]

      5. 总结

      在面试中，另一个常常问的问题就是这两种方法有何优劣。看起来分治法的快速选择算法的时间、空间复杂度都优于使用堆的方法，但是要注意到快速选择算法的几点局限性：

第一，算法需要修改原数组，如果原数组不能修改的话，还需要拷贝一份数组，空间复杂度就上去了。

第二，算法需要保存所有的数据。如果把数据看成输入流的话，使用堆的方法是来一个处理一个，不需要保存数据，只需要保存 k 个元素的最大堆。而快速选择的方法需要先保存下来所有的数据，再运行算法。当数据量非常大的时候，甚至内存都放不下的时候，就麻烦了。所以当数据量大的时候还是用基于堆的方法比较好。

53. 在排序数组中查找数字

1. 思路

  • 字典
    • 用一个字典或者值遍历数组
    • 找到加1

  • 二分

    • image.png

      2. 字典

      1. class Solution:
      2. def search(self, nums: List[int], target: int) -> int:
      3.    if len(nums) is None:
      4.        return nums
      5.    nu = {}
      6.    nu[target] = 0
      7.    for i in nums:
      8.        if  i not in nu:
      9.            nu[i] = 1
      10.        else:
      11.            nu[i] += 1
      12.    return nu[target]
      1. class Solution:
      2. def search(self, nums: List[int], target: int) -> int:
      3.    if len(nums) is None:
      4.        return nums
      5.    nu = 0
      6.    for i in nums:
      7.        if i == target:
      8.            nu += 1
      9.        elif i > target:
      10.            break
      11.    return nu

      3. 二分

      1. class Solution:
      2. def search(self, nums: List[int], target: int) -> int:
      3.    i, j = 0, len(nums) - 1
      4.    while i <= j:
      5.        m = (i + j) //2
      6.        if nums[m] <= target:
      7.            i = m + 1
      8.        else:
      9.            j = m - 1
      10.    right = i
      11.    if j >= 0 and nums[j] != target:
      12.        return 0
      13.    i = 0
      14.    while  i <= j:
      15.        m = (i + j) //2
      16.        if nums[m] < target:
      17.            i = m + 1
      18.        else:
      19.            j = m - 1
      20.    left = j
      21.    return right - left -1

      4. 总结

  • 遍历这种方法需要O（n）的时间复杂度，二分查找需要O（logn）的时间复杂度，二分是这道题的最优解

  • 二分法要注意右边的判断条件是 num[m] <= target， 左边的是 nums[m] < target

57. 和为s的两个数字

1. 思路

  • 字典
    • 把target-num作为key保存到字典中，遍历看是否有满足的

  • 双指针

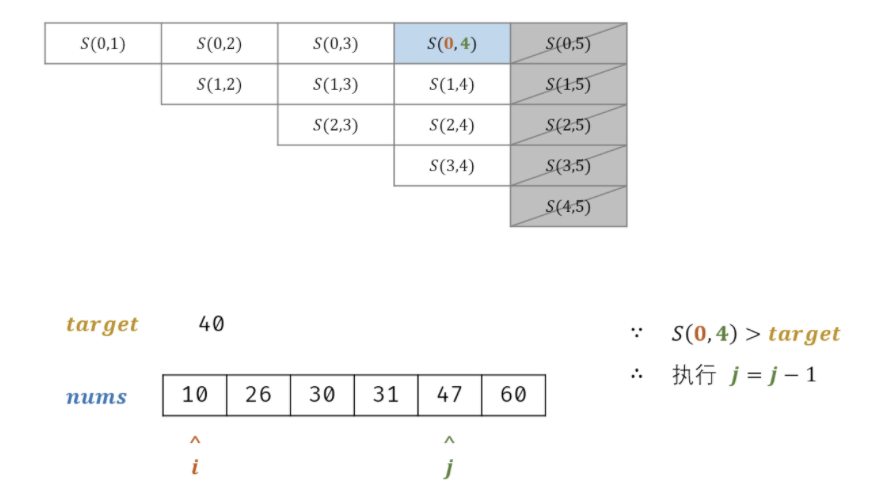
    • image.png
    • image.png

      2. 字典

      1. class Solution:
      2. def twoSum(self, nums: List[int], target: int) -> List[int]:
      3.    partner = {}
      4.    for i in nums:
      5.        if i in partner:
      6.            return [i, partner[i]]
      7.        else:
      8.            partner[target - i] = i
      9.    return []

      3. 双指针

      1. class Solution:
      2. def twoSum(self, nums: List[int], target: int) -> List[int]:
      3.    i, j = 0, len(nums) - 1
      4.    while i < j:
      5.        s = nums[i] + nums[j]
      6.        if s > target: j -= 1
      7.        elif s < target: i += 1
      8.        else: return nums[i], nums[j]
      9.    return []

      4. 总结

  • 这两种方法的时间复杂度都是O(n)，字典的空间复杂度为O(n)，双指针的空间复杂度为O(1)