树是一种分层数据的抽象模型
- 现实生活中最常见的树的例子是家谱或是公司的组织架构图
一个树结构包含一系列存在父子关系的节点
- 每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点
下面为完全二叉树的示例:
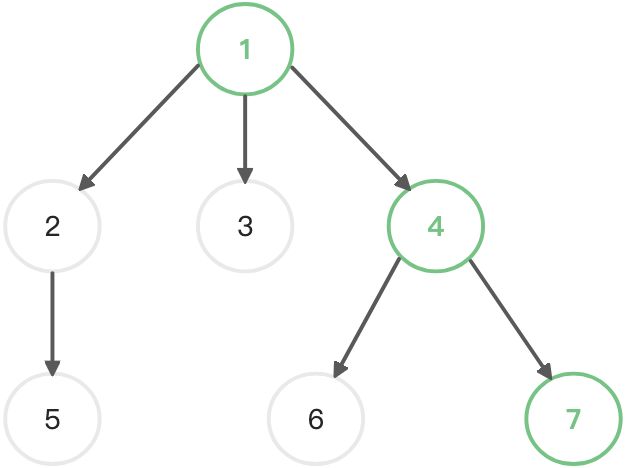
用代码来表示上述 树节点 ```tsx // 链表节点 class ListNode { val: number next: ListNode | null
constructor(val?: number, next?: ListNode | null) { this.val = (val === undefined ? 0 : val) this.next = (next === undefined ? null : next) } }
// 树节点 class TreeNode { val: number child: TreeNode[] | null
constructor(val?: number, child?: TreeNode[] | null) { this.val = (val === undefined ? 0 : val) this.child = (child === undefined ? null : left) } }
- 可以看到,链表就是一种特殊的树结构- 如图中:1->4->7->null- 树的有一个重要属性叫 `度`,指的就是每个节点的子节点个数- 图中,1 号节点的度为 3,2号节点的度为 1,3 号节点的度为 0,4 号节点的度为 2<a name="KJVVp"></a># 二叉树- 二叉树的特性- 每个节点的度最多为 2- 度为 0 的节点比度为 2 的节点数量上多 1 个
证:
1、很明显,n 个节点的树,有 n-1 条边 2、度为 0 的节点记为 n0,度为 1 的节点记为 n1,度为 2 的节点记为 n2,所以 n0 + n1 + n2 = n 3、树的所有边的数量为 n0 0 + n1 1 + n2 2 = n - 1 4、n0 + n1 + n2 - 1 = n1 + 2 n2 5、n0 = n2 + 1
- 二叉树的三种重要遍历
- 前序遍历
- 根 -> 左子树 -> 右子树
- 中序遍历
- 左子树 -> 根 -> 右子树
- 后序遍历
- 左子树 -> 右子树 -> 根
- 通过`中序遍历`的结果和`前序/后序遍历`的结果,可以还原二叉树
- 当然还有其他遍历方式,如层序遍历等
<a name="klBCu"></a>
## 完全二叉树
- complete binary tree
- 只有在树的最后一层的右侧缺少节点的这类二叉树,才叫做完全二叉树
- 特性:
- 树的根节点以 1 为初始编号,那么编号为 i 的子节点:
- 左孩子节点的编号为:2 * 1
- 右孩子节点的编号为:2 * i + 1
- 完全二叉树可以节省用于存储 `边` 的空间,因为通过节点编号可以计算出其子节点的编号
- 可以用连续空间进行存储,如数组
- 下面为完全二叉树的示例:
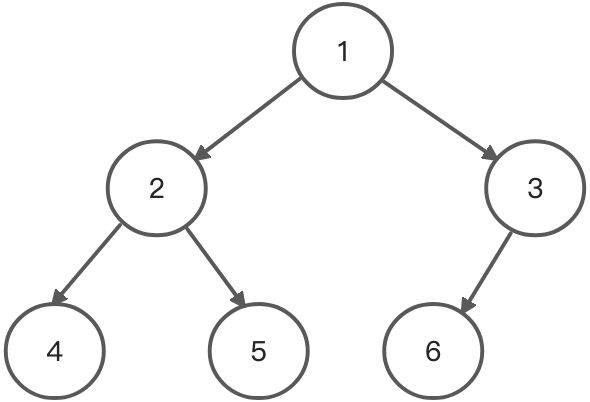
<a name="XfiWH"></a>
## 满二叉树
- full binary tree
- 没有 `度 为 1` 的节点的二叉树
- 下面为满二叉树的示例:
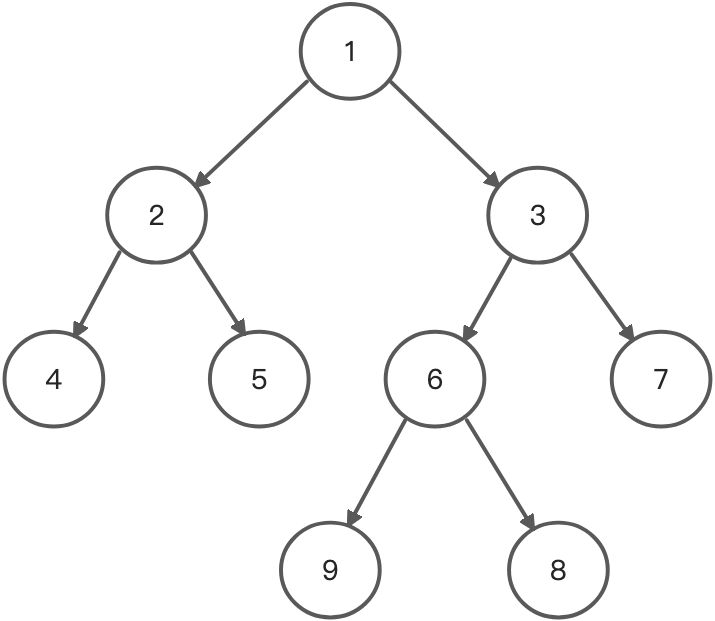
<a name="V0Tkf"></a>
## 完美二叉树
- perfect binary tree
- 每一层节点都是满了的二叉树
- 下面为完美二叉树的示例:
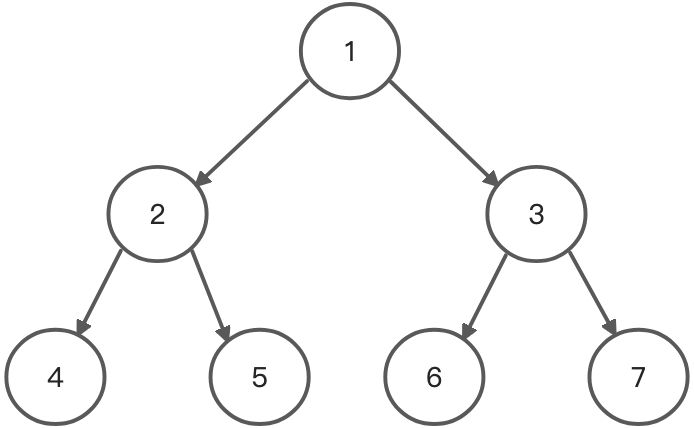
<a name="QQxfy"></a>
# 关于树结构的深入理解
- 节点代表的是集合,边代表的是节点之间的关系
- 父节点就是全集,各个子节点就是互不相交的子集
- 所有子节点代表的子集,加起来就等于,父节点代表的全集
- 集合涉及到的最基础的问题就是查找,而树结构一般情况下,是适用于各种场景下的查找操作
<a name="P3d1e"></a>
# 二叉树的作用
<a name="KaDBe"></a>
## 是理解高级数据结构的基础
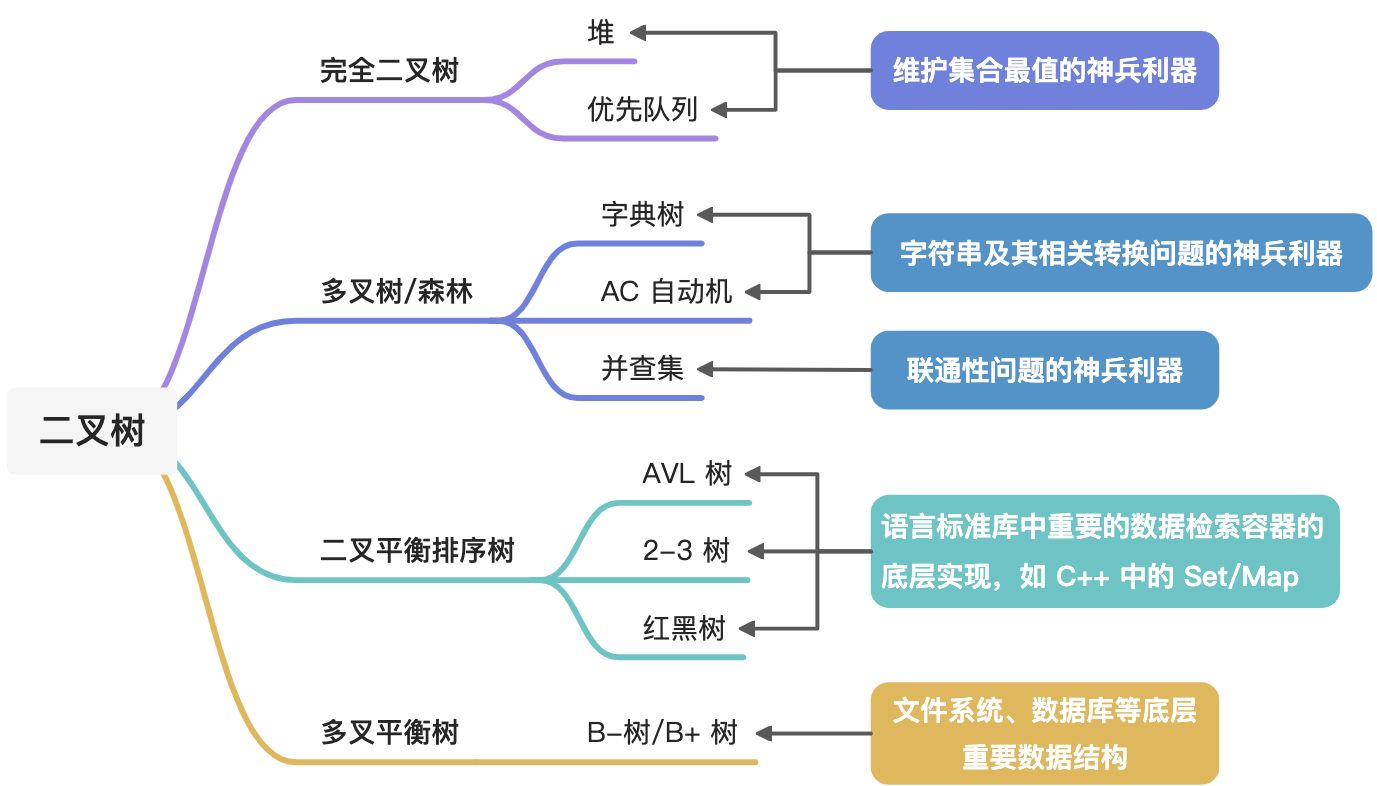
<a name="DFgxd"></a>
## 是练习递归技巧的最佳选择
- 设计/理解递归程序:
1. 赋予递归函数一个明确的意义
1. 思考边界边界条件
1. 实现递归过程
1. 数学归纳法,也叫结构归纳法
1. 确定 k0 是正确的,也就是边界条件正确
1. 假设 k(i) 正确,能推导 k(i + 1) 也正确
- 举个例子 🌰,求斐波那契数列中的第 n 个数字
1. 函数意义:第 n 项斐波那契数列的数字
1. 边界条件:n 为 1 或者 n 为 2 时,直接返回 n
1. 递归过程:函数返回 f(n - 1) + f(n - 2)
1. 数学归纳法证明
1. 确定 k(0) 是正确的,也就是输入 边界条件 得出的结果是正确的
1. 假设 k(n-1) 与 k(n-2) 都是正确的,可以推导出 k(n) = k(n-1) + k(n-2) 是正确的
1. 所以下面的递归程序是正确的
```jsx
const fb = (n) => {
if(n <= 2) return n;
return fb(n - 1) + fb(n - 2)
}
可以节省存储空间
- 使用左孩子右兄弟表示法可以节省存储空间
左孩子右兄弟表示法,指的是将一颗树,转换为二叉树的形式
- 该树的根节点不变
- 树中节点的左孩子为原树的当前节点的左孩子
- 树中节点的右孩子为原树的当前节点的兄弟节点
下图左边是一颗 多叉树,右边是该树的左孩子右兄弟表示法表示的二叉树
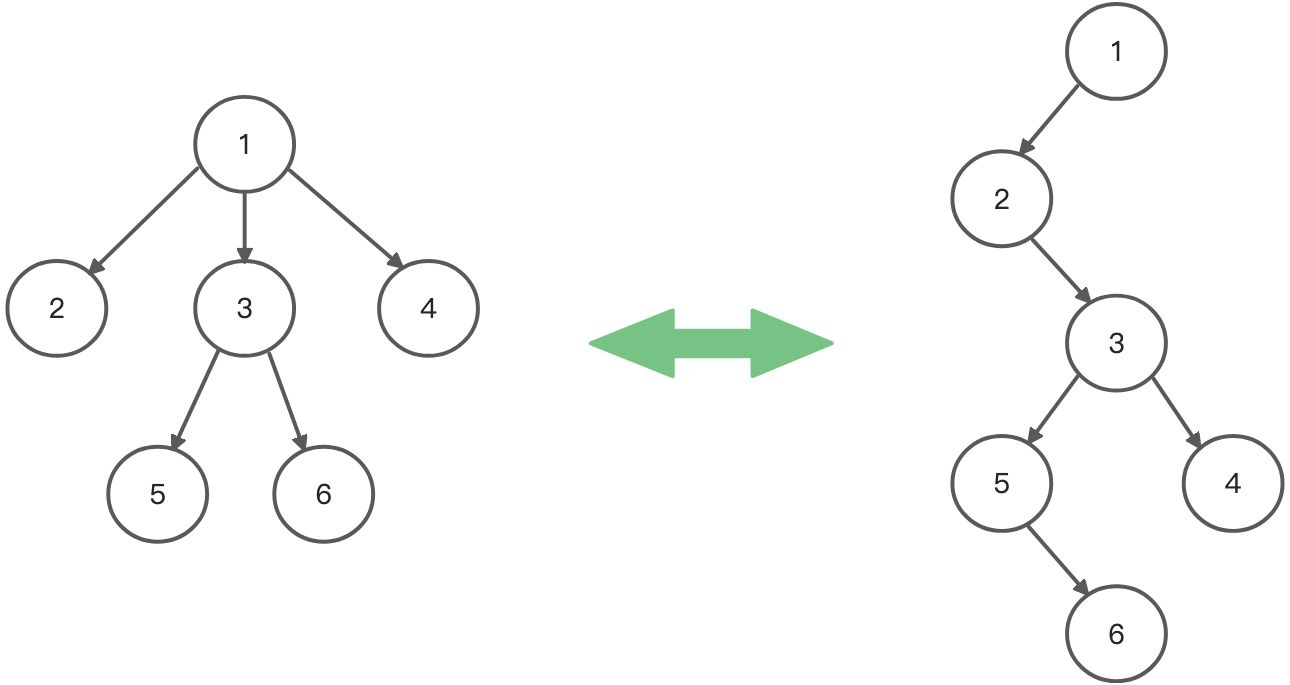
上述方法为什么可以节省树的存储空间?
上图两颗树
- 假设左边树是三叉树,每个节点拥有 3 个指针域,且该树有 6 个节点,5 条边
- 由于不是每个节点的每个指针域都是被使用的
- 计算可得左树总共浪费的指针域的数量为:6 * 3 - 5 = 13
- 右边树为二叉树,每个节点拥有 2 个指针域,且该树有 6 个节点,5 条边
- 计算可得右树总共浪费的指针域的数量为:6 * 2 - 5 = 7
- 所以,上述右树相比于左树,是节约了存储空间的
- 假设左边树是三叉树,每个节点拥有 3 个指针域,且该树有 6 个节点,5 条边
一个有 n 个节点的 k 叉树
- 其指针域总数量为 n * k
- 其边的数量为 n - 1,也就是有 n - 1 个指针域被使用
- 浪费的指针域数量为:n k - (n - 1) = (k -1) n + 1

