ARTS是什么? Algorithm：每周至少做一个LeetCode的算法题 Review：阅读并点评至少一篇英文技术文章 Tip：学习至少一个技术技巧,总结和归纳日常工作中遇到的知识点 Share：分享一篇有观点和思考的技术文章

Algorithm

完成动态规划的相关题目

  1. /**
  2.  * 0-1背包问题
  3.  * 我们有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。
  4.  * 我们现在期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量最大？
  5.  *
  6.  * 动态规划
  7.  * @author ohYoung
  8.  * @date 2021/12/2 23:03
  9.  */
  10. public class MyZero2OneBagDynamic {
  12.     /**
  13.      * 存储背包中物品总量的最大值
  14.      */
  15.     public int maxWeight = Integer.MIN_VALUE;
  17.     /**
  18.      * 动态规划的方式实现0-1背包问题
  19.      * @param weight 物品重量
  20.      * @param totalCount 物品个数
  21.      * @param maxWeight 背包总承重
  22.      * @return 能放入背包的最大总重量
  23.      */
  24.     public int knapsack(int[] weight, int totalCount, int maxWeight) {
  25.         boolean[][] states = new boolean[totalCount][maxWeight + 1];
  26.         // 第一行特殊处理
  27.         // 第一个物品不加入背包
  28.         states[0][0] = true;
  29.         // 第一个物品加入背包
  30.         if (weight[0] <= maxWeight) {
  31.             states[0][weight[0]] = true;
  32.         }
  33.         // 动态规划转移, 第一行已处理, i从1开始
  34.         for (int i = 1; i < totalCount; i++) {
  35.             // 第i行不放入背包
  36.             for (int j = 0; j <= maxWeight; j++) {
  37.                 if (states[i - 1][j]) {
  38.                     states[i][j] = true;
  39.                 }
  40.             }
  41.             // 第i行放入背包
  42.             for (int j = 0; j <= maxWeight - weight[i]; j++) {
  43.                 if (states[i - 1][j]) {
  44.                     states[i][j + weight[i]] = true;
  45.                 }
  46.             }
  47.         }
  48.         // 输出结果
  49.         for (int i = maxWeight; i > 0; i--) {
  50.             if (states[totalCount - 1][i]) {
  51.                 return i;
  52.             }
  53.         }
  54.         return 0;
  55.     }
  57.     /**
  58.      * knapsack方法需要一个totalCount*(maxWeight+1)大小的数组, 这个方法主要优化这个空间消耗
  59.      */
  60.     public int knapsack2(int[] weight, int totalCount, int maxWeight) {
  61.         boolean[] states = new boolean[maxWeight + 1];
  62.         states[0] = true;
  63.         if (weight[0] < maxWeight) {
  64.             states[weight[0]] = true;
  65.         }
  66.         // 动态规划
  67.         for (int i = 0; i < totalCount; i++) {
  68.             // 把第i个物品放入背包
  69.             for (int j = maxWeight - weight[i]; j >= 0; j--) {
  70.                 if (states[i]) {
  71.                     states[j + weight[i]] = true;
  72.                 }
  73.             }
  74.         }
  75.         // 输出结果
  76.         for (int i = maxWeight; i >= 0; i--) {
  77.             if (states[i]) {
  78.                 return i;
  79.             }
  80.         }
  81.         return 0;
  82.     }
  84.     public static void main(String[] args) {
  85.         MyZero2OneBagDynamic example = new MyZero2OneBagDynamic();
  86.         int[] items = new int[]{1, 4, 7};
  87.         System.out.println(example.knapsack(items, items.length, 10));
  88.     }
  89. }

Review

What’s New in IntelliJ IDEA 2021.3
IDEA 2021.3推出的新功能：

  1. 支持远程开发功能（测试版本）
  2. 当你感觉的IDE出问题的时候可以通过File->Repair IDE按钮快速修复IDE的问题
  3. 新增选项，允许同时修改活动窗口的字体大小（Preferences/ Settings | Editor | General, choose Change font size with Command + mouse wheel in, and select All editors）
  4. 现在的提示视图更加清晰，会更加清楚的提示你当前操作带来的结果是什么

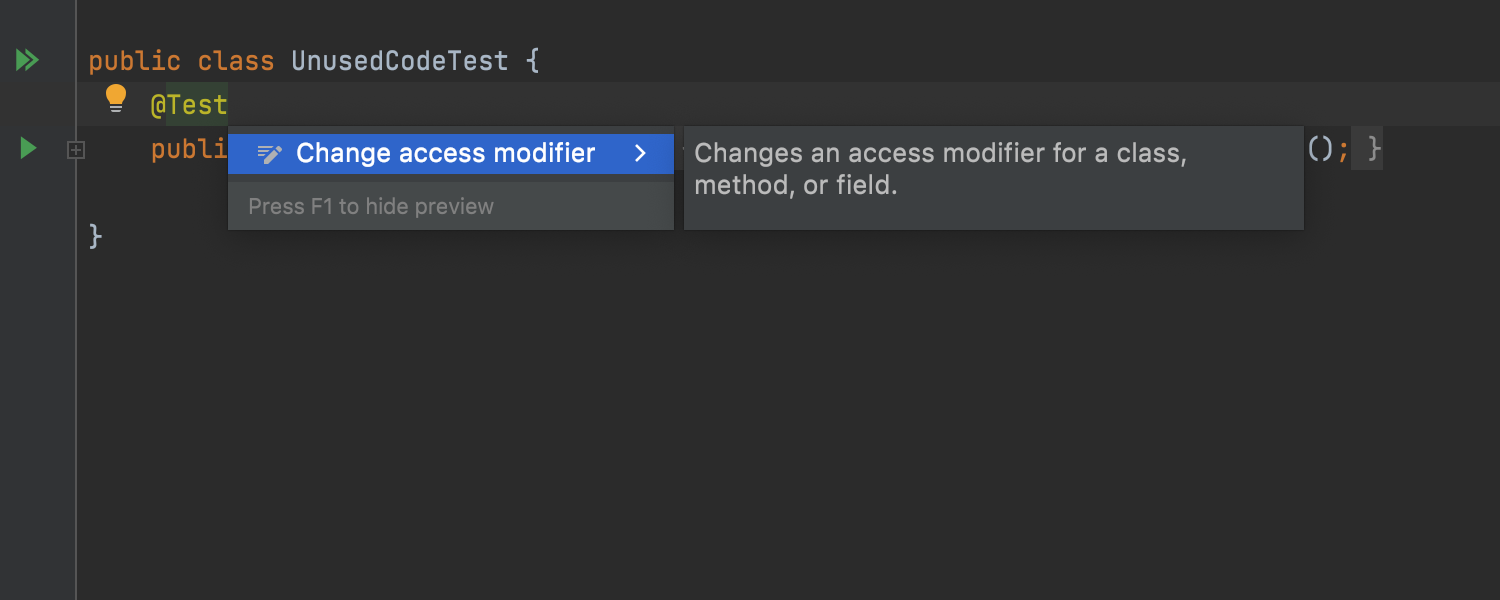
ARTS - 第17周 - 图1

  1. markdown体验提升，比如现在可以更加方便的添加表格了
  2. 右上角新增【三个点】按钮，点击可以选择一些快捷操作
  3. 关于Java的更新
    1. 支持追踪不安全的字符串参数的检查，其他新的检查：例如提示将collect(toList())改为.toList()
    2. 重构升级，例如：我们现在在提取公共变量的同时可以选择将变量置为final
    3. 支持自定义run/debug的类路径

其他的自行查阅。

Tip

  1. DDD中有两个概念聚合和组合。我理解其最大的区别是聚合可以拆开，实体各自不受影响。但是组合不行，拆开就不能单独运转了。例如，房屋有分期、分区、楼栋的概念，但是房屋没有分期、分区或楼栋也是能玩的，这些概念实体是可以单独运转的，它们是聚合关系。但是一辆车的实体比如车轮、发动机等，就不可以运转了，这就是组合关系。
  2. 《中台架构与实现》中要求微服务内使用事件总线（异步）的方式进行解耦，微服务之间用中间件的方式进行解耦。个人认为太绝对，不同的业务场景完全可以使用更加简洁的办法，例如我的业务不需要异步提高效率，那么我就可以使用观察者模式同步调用事件。这样我的代码解耦了，同时页不需要考虑异步情况下的数据补偿机制。

    Share

    DDD建模工作坊指南
    这里介绍了大量DDD相关的概念以及如何开展事件风暴。是入门DDD极好的资料。

    Finish

    预计完成时间：2021.12.06 ~ 2021.12.12
    实际完成时间：2021.12.09