数学运算

题目一览图

零、数学运算概述

【数学问题】往往会借助一些数学基本理论 。

一、进制问题

类型概述

【进制问题】往往考察对进制的理解程度，一般来说，题目会用数组/链表/字符串 来存储各位数。

题型一 | 加减乘除

题型串联

1 加一

【概述】数学问题
【题目描述**】
给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外，这个整数不会以零开头。
【题目示例**】

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

【题目分析**】**
本题要求计算十进制加一后的结果。思路比较简单，从两数组的低位开始相高位遍历，对应低位相加，加和除 10 的余数即为当前位输出，加和除 10 的商即为进位。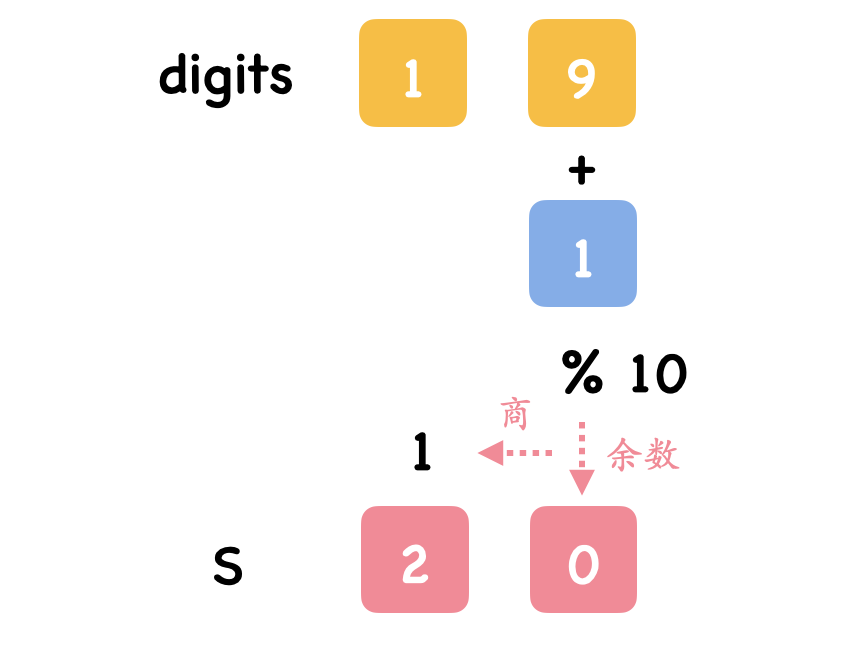

var plusOne = function(digits) {
    let i = digits.length , s = 1;
    while( i-->=0 || s ){
        s += digits[i];
        digits[i] = s % 10;
        s = s / 10 | 0;
        if( i<=0 && s ) digits.unshift(s);
    }
    return digits;
};

2 两数相加

【概述】数学问题
【题目描述**】
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。请你将两个数相加，并以相同形式返回一个表示和的链表。你可以假设除了数字 0 之外，这两个数都不会以 0 开头。
【题目示例**】

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

【题目分析**】**
本题要求通过给出的链表计算出两者和。思路比较简单，由于链表是逆序存储，直接同时遍历链表，对应加和除 10 的余数即为当前位输出，加和除 10 的商即为进位。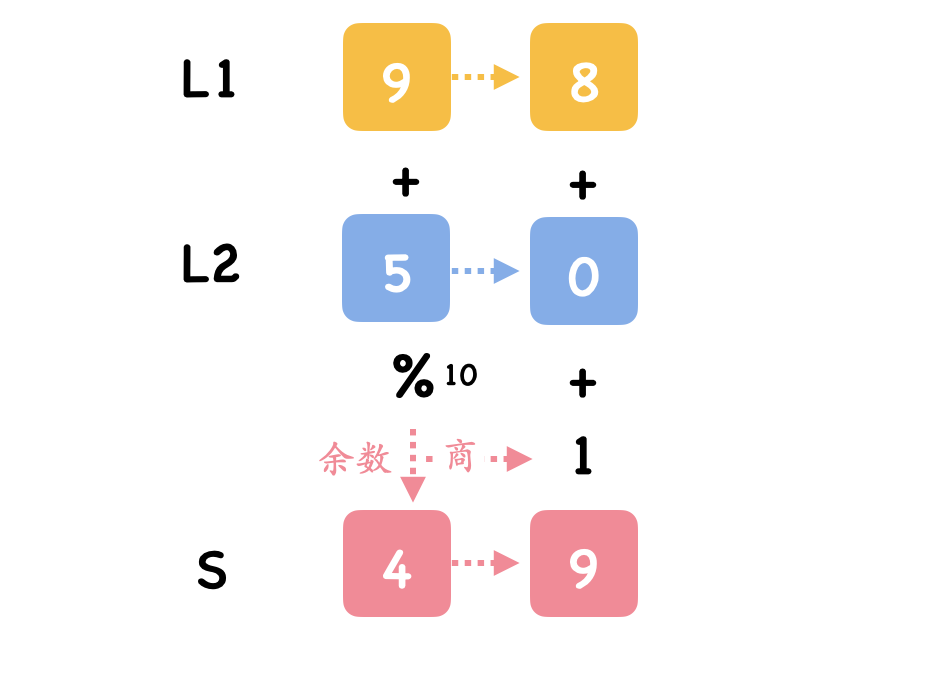

var addTwoNumbers = function(l1, l2) {
    const dummy = new ListNode();
    let sum = 0 , cur = dummy;

    while(l1||l2||sum){
        if(l1) sum+=l1.val,l1 = l1.next;
        if(l2) sum+=l2.val,l2 = l2.next;
        cur.next = new ListNode(sum%10);
        cur = cur.next;
        sum = Math.floor(sum/10);
    }
    return dummy.next;
};

3 二进制求和

【概述】数学问题
【题目描述**】
给你两个二进制字符串，返回它们的和（用二进制表示）。输入为 非空 字符串且只包含数字 1 和 0。
【题目示例**】

输入: a = "11", b = "1"
输出: "100"

【题目分析**】**
本题要求通过给出的字符串计算出两者和。思路比较简单，从两串的低位开始相高位遍历，对应低位相加，加和除 2 的余数即为当前位输出，加和除 2 的商即为进位。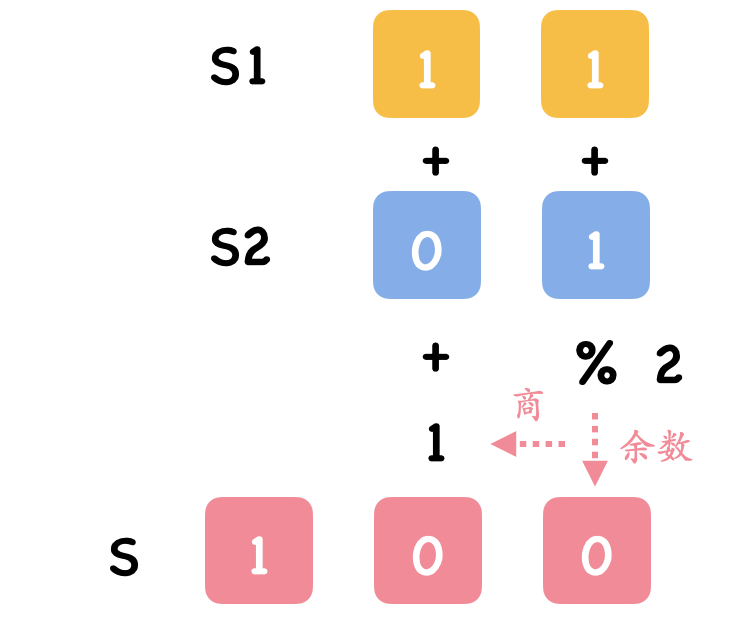

var addBinary = function(a, b) {
    let i = a.length - 1, j = b.length - 1, s = 0;
    let res = '';
    while(i>=0 || j>=0 || s ){
        if(i>=0) s += a[i] - '0';
        if(j>=0) s += b[j] - '0';
        res = ( s % 2 ) + res;
        s = s / 2 | 0;
        i--,j--;
    }
    return res;
};

4 整数反转

【概述】数学问题
【题目描述**】
给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。
【题目示例**】

输入：x = 123
输出：321

【题目分析**】*
本题要求将高低位进行交换。对进制计算的基本考量，具体做法为通过求余和求商将最低分分离，然后通过`res = res 10 + 最低位` 实现数字重组。

var reverse = function(x) {
    let res = 0;

    while(x){
        res = res * 10 + x % 10;
        x =  x / 10 | 0;
    }
    return (res | 0) === res ? res : 0;
};

5 回文数

【概述】数学问题
【题目描述**】
判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。
【题目示例**】

输入: 121
输出: true

【题目分析**】**
本题要求判断是否回文。简单的【整数反转】的应用，只要反转后相同即为同问数。

var isPalindrome = function(x) {
    if(x<0) return false;
    let res = 0 , temp = x;
    while(temp){
        res = res * 10 + temp % 10;
        temp = temp /10 | 0;
    }
    return x === res; 
};

6 字符串相乘

【概述】数学问题
【题目描述**】
给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。
【题目示例**】

输入: num1 = "2", num2 = "3"
输出: "6"

【题目分析**】*
本题要求通过给出的字符串计算出两者乘积。我们需要用加法进行迁移，为了方便说明我们设两个字符串为 num1 num2 ，并且分别用索引 i j 表示（从 0 开始），对应下图 num1[1] 就是 3 。可以看出 `num1[i]num2[j]会影响i+j位，也就是说最终结果是(num1[i]num2[j])10^(i+j)`i j 遍历的叠加。所以我们可以穿件一个 i+j 长的数组，将每一位存储进去最后进行叠加。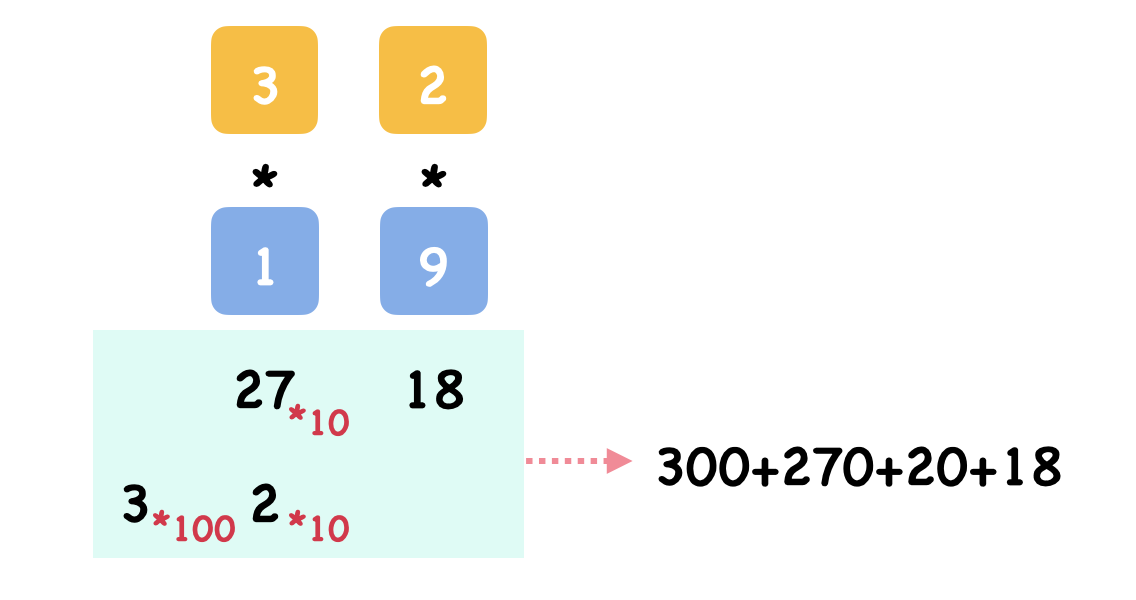

var multiply = function(num1, num2) {
    const a = [] , b = [];
    const m = num1.length , n = num2.length ;

    for( let i = m - 1 ; i >= 0 ; i--) a.push(num1[i]-'0');
    for( let i = n - 1 ; i >= 0 ; i--) b.push(num2[i]-'0');

    const c = new Array(m+n).fill(0);
    for( let i = 0 ; i < m ; i++){
        for( let j = 0 ; j < n ; j++){
            c[i+j] += a[i] * b[j];
        }
    }

    for(let i = 0 , t = 0; i < m+n ; i++){
        t += c[i],c[i] = t % 10,t = ( t / 10 ) | 0;
    }

    let k = c.length - 1 ,res = '';
    while(k > 0 && !c[k]) k--;
    while(k>=0) res += c[k--]+ '';
    return res;
};

题型二 | 特殊进制

题型串联

1 整数转罗马数字

【概述】数学问题
【题目描述**】**
罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。
【题目示例**】**

输入: 3
输出: "III"

【题目分析**】**
本题要求整数转罗马数组。对罗马数字陌生的话，就可以将其理解为一种新的进制规则，在 9 5 4 1 这四个地方有独特的取值，所以我们列出个字典对照即可。

var intToRoman = function(num) {
    const values = [
        1000,
        900, 500, 400, 100,
        90, 50, 40 , 10,
        9, 5, 4, 1],
        reps = [
            "M",
            "CM", "D", "CD", "C",
            "XC", "L", "XL", "X",
            "IX", "V", "IV", "I",
        ];

    let res = '';
    for(let i = 0 ; i<= 12 ; i++){
        while(num>=values[i]){
            num -= values[i];
            res += reps[i];
        }
    }
    return res;
};

2 整数转罗马数字

【概述】数学问题
【题目描述**】**
罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。
【题目示例**】**

输入: "III"
输出: 3

【题目分析**】**
本题要求罗马数字转数字组。与【整数转罗马数字】相同，在 9 5 4 1 这四个地方有独特的取值，但是需要注意的是 4 IV 和 9 IX 那？可以发现，与其他数不同，如果符号小的在符号大的的左边，就是减去，比如 IV 就是 V - I ，而 VI 就是V + I 。

var romanToInt = function(s) {
    const map = {
        'I':1,
        'V':5,
        'X':10,
        'L':50,
        'C':100,
        'D':500,
        'M':1000,
    }

    let res = 0 ;
    for(let i = 0 ; i < s.length ; i++){
        if(map[s[i]]<map[s[i+1]]) res -= map[s[i]];
        else res += map[s[i]];
    } 
    return res;
};

二、常用技巧

类型概述

【常用技巧】是指在做题中有一些有用的小技巧，帮助我们快速得到答案。
【快速幂】这是一种时间复杂度为 O(logn) 的算法，利用十进制数字 n 的二进制表示，可对快速幂进行数学化解释。对于任何十进制正整数 n ，

• 【二进制】 bm...b3b2b1
• 【十进制】 n=bm*2^m+...b3*2^3+b2*2^2+b1*2

• 【循环】所以我们可以用 2 的幂次方 将 一个较大的数 拆成 多项式求和。

  • 循环操作为x = x + x ，即 2 的幂次方。
  • 获取二进制各位的值
    • n & 1 - 判断 n 二进制最右一位是否为 1
    • n >> 1 - n 右移一位（可理解为删除最后一位）

      题型一 | 快速幂

      题型串联

      1 Pow(x, n)

      【概述】数学问题 快速幂
      【题目描述**】
      实现 pow(x, n) ，即计算 x 的 n 次幂函数。
      【题目示例**】

      输入: 2.00000, 10
      输出: 1024.00000
      

      【题目分析**】**
      本题要求计算x的n次幂。该题为【快速幂】的基本例题，唯一值得注意的是有正负号的问题。

      var myPow = function(x, n) {
      if( n < 0) return 1/myPow(x,-n);
      let k = n , res = 1;
      while(k){
      if(k&1)res *= x;
      x *= x;
      k >>>= 1;
      }
      return res;
      };
      

      2 两数相除

      【概述】数学问题
      【题目描述**】
      给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数 divisor 得到的商。
      【题目示例**】

      输入: dividend = 10, divisor = 3
      输出: 3
      解释: 10/3 = truncate(3.33333..) = truncate(3) = 3
      

      【题目分析**】*
      本题要求计算两数之商。直接想比较复杂，我们可以先通过反计算-乘法思考。乘法可以理解为多个数相加，那除法就可以使用多个数的和/积去近似。为了更快的近似，我们借助幂指数实现（指数递增），将商拆成幂指数加和，即`n divisor = (bm2^m+…b32^3+b22^2+b12) * divisor` 变成一个可以递归的式子。
      PS ： 要考虑正负号。 ```javascript var divide = function(x, y) { const exp = []; let sign = false; if( x < 0 && y > 0 || x > 0 && y < 0 ) sign = true;

  let a = Math.abs(x) , b = Math.abs(y); for( let i = b ; i <= a ; i = i+i ) exp.push(i);

  let res = 0 , flag = false ; for( let i = exp.length - 1 ; i >= 0 ; i—){ if(i>=31){ flag = true; break;} if( a >= exp[i]){

     a -= exp[i];
     res += 1 << i ;
  

  } } if(flag) res = sign ? -2147483648 : 2147483647; else res = sign ? -res : res;

  if(res>Math.pow(2,31)-1||res<Math.pow(-2,31))return Math.pow(2,31)-1 return res; };

  <a name="lK3Mx"></a>
  ### 题型二 | 位运算
  <a name="284up"></a>
  #### 题型串联
  <a name="hNcaw"></a>
  #### 1 [只出现一次的数字](https://leetcode-cn.com/problems/single-number/)
  **【概述】数学问题 异或**<br />**【题目描述****】**<br />给定一个**非空**整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。<br />**【题目示例****】**
  

  输入: [2,2,1] 输出: 1

  **【题目分析****】**<br />本题要求找出只出现一次的数。本题考查异或的基本用法，即与本身异或是 `0` ， `a^a = 0` ，与 `0` 异或是本身， `a^0 = a`。由于只有一个数出现一次，其他都是出现两次，如果将数组里的数都被异或操作，两个都变 `0` ，只留下出现一次的。
  ```javascript
  var singleNumber = function(nums){
  let res = 0;
  for( let num of nums){
     res ^= num;
  }
  return res;
  };
  

  2 只出现一次的数字

  【概述】数学问题 异或
  【题目描述**】
  给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。
  【题目示例**】

  输入: [2,2,3,2]
  输出: 3
  

  【题目分析**】**
  本题要求找出只出现一次的数。由于本题其他数出现三次，所以单纯异或行不通了，需要更多状态的引入。首先我们从状态入手，当前有三个状态 0 1 2 ，我们希望 2 状态再来一个会回到 0 状态，即三个自相残杀全没了。由于是要位运算，我们将 0 1 2 编码为 00 01 10 ，然后就看看怎么计算才能实现状态转移。
  假设当前加的数是 num ，我们可以将其看成一个二进制数，由于每一位的计算方式是一样的，我们不妨将其一位认作是 n ，通过探索 n 的转移关系，进而得到整个 num 的转移关系。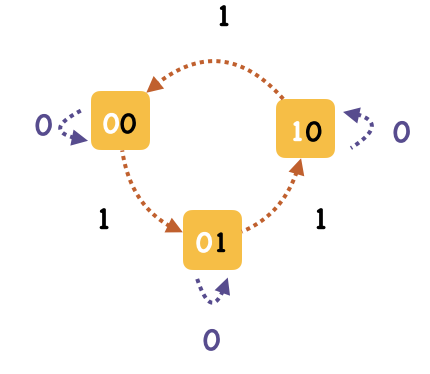
  
  如上图所示，我们假设00 01 10 低位为 once （白），高位为 twice （黑）。

• 已知的公式

  • x ^ 0 = x x ^ 1 = ~x
  • x & 0 = 0 x & 1 = x
• 可以发现
  • twice===0 时， once=one^n
  • twice===1 时， once=0
    
  • 合并为 once = once ^ n & ~twice
• 同理 twice = once ^ n & ~once

所以根据转态转移式，得到最终代码。

var singleNumber = function(nums) {
    let once = 0 , twice = 0;
    for( let num of nums ){
        once = (once^num)&(~twice);
        twice = (twice^num)&(~once);
    }
    return once;
};