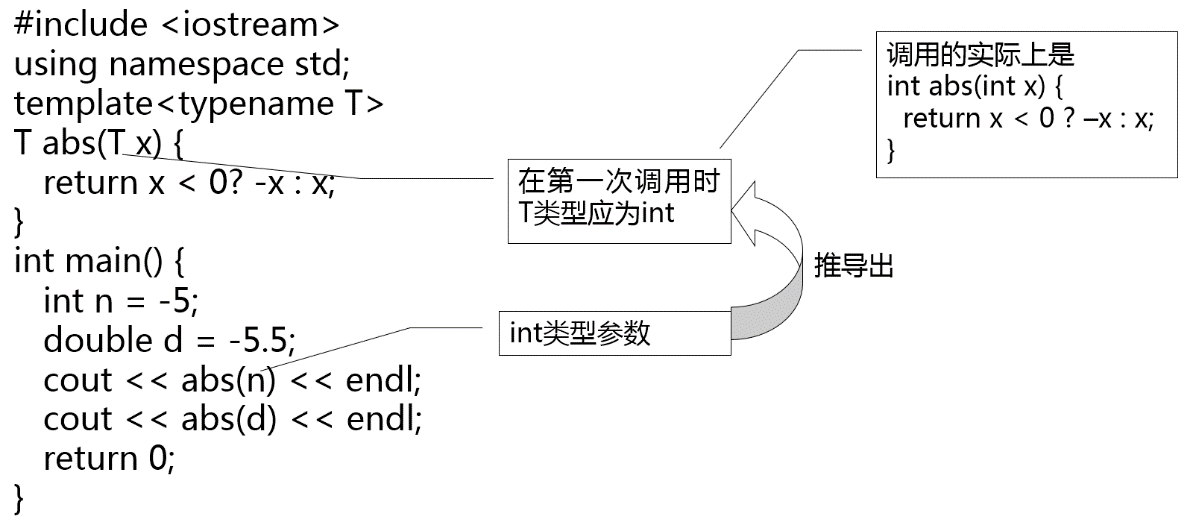
一、模板
函数的形参可以让函数处理不同数值的数据,模板可以让函数处理不同类型的数据。
原理上,一个模板会生成一些列不同类型形参的同名函数
函数模板
解决问题:如果重载的函数,其解决问题的逻辑是一致的、函数体语句相同,只是处理的数据类型不同,那么写多个相同的函数体,是重复劳动,而且还可能因为代码的冗余造成不一致性。
语法形式:template <模板参数表>
- 类型参数:class(或typename) 标识符
- 常量参数:类型说明符 标识符
- 模板参数:template <参数表> class标识符
注意
- 一个函数模板并非自动可以处理所有类型的数据。只有能够进行函数模板中运算的类型,可以作为类型实参
- 自定义的类,需要重载模板中的运算符,才能作为类型实
template<class out_type,class in_value>out_type convert(const in_value & t){stringstream stream;stream<<t;//向流中传值out_type result;//这里存储转换结果stream>>result;//向result中写入值return result;}int main(){double d;string salary;string s="12.56";d=convert<double>(s);//d等于12.56salary=convert<string>(9000.0);//salary等于”9000”return 0;}
类模板
类模板通过实例化以后的对象被称为模板类
类模板的作用
使用类模板使用户可以为类声明一种模式,使得类中的某些数据成员、某些成员函数的参数、某些成员函数的返回值,能取任意类型(包括基本类型的和用户自定义类型)。
类模板的声明
- 类模板 template <模板参数表> class 类名 {类成员声明};
- 如果需要在类模板以外定义其成员函数,则要采用以下的形式: template <模板参数表> 类型名 类名<模板参数标识符列表>::函数名(参数表) 【其实就是在正常情况多一个类模板声明】
例9-2 类模板示例
#include <iostream>#include <cstdlib>using namespace std;struct Student {int id; //学号float gpa; //平均分};template <class T>class Store {//类模板:实现对任意类型数据进行存取private:T item; // item用于存放任意类型的数据bool haveValue; // haveValue标记item是否已被存入内容public:Store();T &getElem(); //提取数据函数void putElem(const T &x); //存入数据函数};template <class T>Store<T>::Store(): haveValue(false) { }template <class T>T &Store<T>::getElem() {//如试图提取未初始化的数据,则终止程序if (!haveValue) {cout << "No item present!" << endl;exit(1); //使程序完全退出,返回到操作系统。}return item; // 返回item中存放的数据}template <class T>void Store<T>::putElem(const T &x) {// 将haveValue 置为true,表示item中已存入数值haveValue = true;item = x; // 将x值存入item}int main() {Store<int> s1, s2;s1.putElem(3);s2.putElem(-7);cout << s1.getElem() << " " << s2.getElem() << endl;Student g = { 1000, 23 };Store<Student> s3;s3.putElem(g);cout << "The student id is " << s3.getElem().id << endl;Store<double> d;cout << "Retrieving object D... ";cout << d.getElem() << endl;//d未初始化,执行函数D.getElement()时导致程序终止return 0;}
二、线性群体
群体是指由多个数据元素组成的集合体。群体可以分为两个大类:线性群体和非线性群体。
- 线性群体中的元素按位置排列有序,可以区分为第一个元素、第二个元素等。
- 线性群体中的元素次序与其逻辑位置关系是对应的。在线性群体中,又可按照访问元素的不同方法分为
- 直接访问 ,比如下标
- 顺序访问,比如节点
- 索引访问
- 线性群体中的元素次序与其逻辑位置关系是对应的。在线性群体中,又可按照访问元素的不同方法分为
- 非线性群体不用位置顺序来标识元素。
在本章我们只介绍直接访问和顺序访问。
- 顺序表、链表、栈、队列均是线性结构
- 而树和图非线性
三、数组
- 静态数组是具有固定元素个数的群体,其中的元素可以通过下标直接访问。
- 缺点:大小在编译时就已经确定,在运行时无法修改。
- 动态数组由一系列位置连续的,任意数量相同类型的元素组成。
- 优点:其元素个数可在程序运行时改变。
- vector就是用类模板实现的动态数组。
数组就是通过物理上的连续存放关系(内存地址相邻),维持逻辑上的连续,所以可以直接访问。
动态数组类模板程序
这里手动实现一个动态数组,并且体现指针转化运算符的作用
#ifndef ARRAY_H#define ARRAY_H#include <cassert>template <class T> //数组类模板定义class Array {private:T* list; //用于存放动态分配的数组内存首地址int size; //数组大小(元素个数)public:Array(int sz = 50); //构造函数Array(const Array<T> &a); //复制构造函数~Array(); //析构函数Array<T> & operator = (const Array<T> &rhs); //重载"=“T & operator [] (int i); //重载"[]”const T & operator [] (int i) const; //重载"[]”常函数operator T * (); //重载到T*类型的转换operator const T * () const;int getSize() const; //取数组的大小void resize(int sz); //修改数组的大小};template <class T> Array<T>::Array(int sz) {//构造函数assert(sz >= 0);//sz为数组大小(元素个数),应当非负size = sz; // 将元素个数赋值给变量sizelist = new T [size]; //动态分配size个T类型的元素空间}template <class T> Array<T>::~Array() { //析构函数delete [] list;}template <class T>Array<T>::Array(const Array<T> &a) { //复制构造函数size = a.size; //从对象x取得数组大小,并赋值给当前对象的成员list = new T[size]; // 动态分配n个T类型的元素空间for (int i = 0; i < size; i++) //从对象X复制数组元素到本对象list[i] = a.list[i];}//续上,重载"="运算符,将对象rhs赋值给本对象。实现对象之间的整体赋值template <class T>Array<T> &Array<T>::operator = (const Array<T>& rhs) {if (&rhs != this) {//如果本对象中数组大小与rhs不同,则删除数组原有内存,然后重新分配if (size != rhs.size) {delete [] list; //删除数组原有内存size = rhs.size; //设置本对象的数组大小list = new T[size]; //重新分配size个元素的内存}//从对象X复制数组元素到本对象for (int i = 0; i < size; i++)list[i] = rhs.list[i];}return *this; //返回当前对象的引用}//重载下标运算符,实现与普通数组一样通过下标访问元素,具有越界检查功能template <class T>T &Array<T>::operator[] (int n) {assert(n >= 0 && n < size); //检查下标是否越界return list[n]; //返回下标为n的数组元素}template <class T>const T &Array<T>::operator[] (int n) const {assert(n >= 0 && n < size); //检查下标是否越界return list[n]; //返回下标为n的数组元素//重载指针转换运算符,将Array类的对象名转换为T类型的指针template <class T>Array<T>::operator T * () {return list; //返回当前对象中私有数组的首地址}//取当前数组的大小template <class T>int Array<T>::getSize() const {return size;}// 将数组大小修改为sztemplate <class T>void Array<T>::resize(int sz) {assert(sz >= 0); //检查sz是否非负if (sz == size) //如果指定的大小与原有大小一样,什么也不做return;T* newList = new T [sz]; //申请新的数组内存int n = (sz < size) ? sz : size;//将sz与size中较小的一个赋值给n//将原有数组中前n个元素复制到新数组中for (int i = 0; i < n; i++)newList[i] = list[i];delete[] list; //删除原数组list = newList; // 使list指向新数组size = sz; //更新size}#endif //ARRAY_H
#include <iostream>using namespace std;void read(int *p, int n) {for (int i = 0; i < n; i++)cin >> p[i];}int main() {int a[10];read(a, 10);return 0;}----------------------------------------------------#include "Array.h"#include <iostream>using namespace std;void read(int *p, int n) {for (int i = 0; i < n; i++)cin >> p[i];}int main() {Array<int> a(10);read(a, 10);return 0;}
对Array类的应用,求0-n之间的质数:
#include <iostream>#include <iomanip>#include "Array.h"using namespace std;int main() {// 用来存放质数的数组,初始状态有10个元素Array<int> a(10);int n, count = 0;cout << "Enter a value >= 2 as upper limit for prime numbers: ";cin >> n;for (int i = 2; i <= n; i++) { //检查i是否能被比它小的质数整除bool isPrime = true;for (int j = 0; j < count; j++)//若i被a[j]整除,说明i不是质数if (i % a[j] == 0) {isPrime = false; break;}if (isPrime) {if (count == a.getSize())a.resize(count * 2);a[count++] = i;}}for (int i = 0; i < count; i++)cout << setw(8) << a[i];cout << endl;return 0;}
四、链表
顺序访问的线性群体——链表类
- 链表是一种动态数据结构,可以用来表示顺序访问的线性群体。
- 链表是由系列 结点 组成的,结点可以在运行时动态生成。
- 每一个结点包括 数据域 和指向链表中下一个结点的 指针 (即下一个结点的地址)。如果链表每个结点中只有一个指向后继结点的指针,则该链表称为单链表。
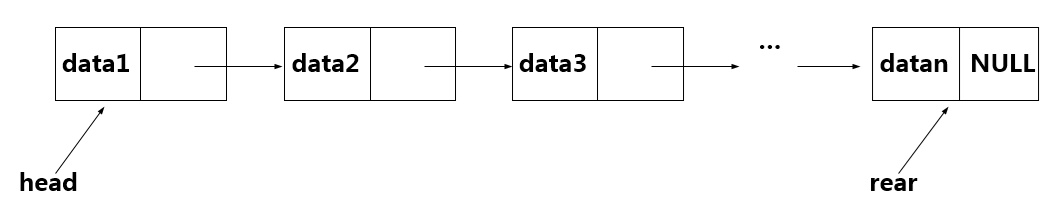
构建链表节点类:
//Node.h#ifndef NODE_H#define NODE_H//类模板的定义template <class T>class Node {private:Node<T> *next; //指向后继结点的指针public:T data; //数据域Node (const T &data, Node<T> *next = 0); //构造函数void insertAfter(Node<T> *p); //在本结点之后插入一个同类结点pNode<T> *deleteAfter(); //删除本结点的后继结点,并返回其地址Node<T> *nextNode(); //获取后继结点的地址const Node<T> *nextNode() const; //获取后继结点的地址};//类的实现部分//构造函数,初始化数据和指针成员template <class T>Node<T>::Node(const T& data, Node<T> *next = 0 ) : data(data), next(next) { }//返回后继结点的指针template <class T>Node<T> *Node<T>::nextNode() {return next;}//返回后继结点的指针template <class T>const Node<T> *Node<T>::nextNode() const {return next;}//在当前结点之后插入一个结点ptemplate <class T>void Node<T>::insertAfter(Node<T> *p) {p->next = next; //p结点指针域指向当前结点的后继结点next = p; //当前结点的指针域指向p}//删除当前结点的后继结点,并返回其地址template <class T> Node<T> *Node<T>::deleteAfter() {Node<T> *tempPtr = next;//将欲删除的结点地址存储到tempPtr中if (next == 0) //如果当前结点没有后继结点,则返回空指针return 0;next = tempPtr->next;//使当前结点的指针域指向tempPtr的后继结点return tempPtr; //返回被删除的结点的地址}#endif //NODE_H
链表的基本操作
- 生成链表
- 插入结点
- 查找结点
- 删除结点
- 遍历链表
- 清空链表
//LinkedList.h#ifndef LINKEDLIST_H#define LINKEDLIST_H#include "Node.h"template <class T>class LinkedList {private://数据成员:Node<T> *front, *rear; //表头和表尾指针Node<T> *prevPtr, *currPtr; //记录表当前遍历位置的指针,由插入和删除操作更新int size; //表中的元素个数int position; //当前元素在表中的位置序号。由函数reset使用//函数成员://生成新结点,数据域为item,指针域为ptrNextNode<T> *newNode(const T &item,Node<T> *ptrNext=NULL);//释放结点void freeNode(Node<T> *p);//将链表L 拷贝到当前表(假设当前表为空)。//被拷贝构造函数、operator = 调用void copy(const LinkedList<T>& L);public:LinkedList(); //构造函数LinkedList(const LinkedList<T> &L); //拷贝构造函数~LinkedList(); //析构函数LinkedList<T> & operator = (const LinkedList<T> &L); //重载赋值运算符int getSize() const; //返回链表中元素个数bool isEmpty() const; //链表是否为空void reset(int pos = 0);//初始化游标的位置void next(); //使游标移动到下一个结点bool endOfList() const; //游标是否到了链尾int currentPosition() const; //返回游标当前的位置void insertFront(const T &item); //在表头插入结点void insertRear(const T &item); //在表尾添加结点void insertAt(const T &item); //在当前结点之前插入结点void insertAfter(const T &item); //在当前结点之后插入结点T deleteFront(); //删除头结点void deleteCurrent(); //删除当前结点T& data(); //返回对当前结点成员数据的引用const T& data() const; //返回对当前结点成员数据的常引用//清空链表:释放所有结点的内存空间。被析构函数、operator= 调用void clear();};template <class T> //生成新结点Node<T> *LinkedList<T>::newNode(const T& item, Node<T>* ptrNext){Node<T> *p;p = new Node<T>(item, ptrNext);if (p == NULL){cout << "Memory allocation failure!\n";exit(1);}return p;}template <class T>void LinkedList<T>::freeNode(Node<T> *p) //释放结点{delete p;}template <class T>void LinkedList<T>::copy(const LinkedList<T>& L) //链表复制函数{Node<T> *p = L.front; //P用来遍历Lint pos;while (p != NULL) //将L中的每一个元素插入到当前链表最后{insertRear(p->data);p = p->nextNode();}if (position == -1) //如果链表空,返回return;//在新链表中重新设置prevPtr和currPtrprevPtr = NULL;currPtr = front;for (pos = 0; pos != position; pos++){prevPtr = currPtr;currPtr = currPtr->nextNode();}}template <class T> //构造一个新链表,将有关指针设置为空,size为0,position为-1LinkedList<T>::LinkedList() : front(NULL), rear(NULL),prevPtr(NULL), currPtr(NULL), size(0), position(-1){}template <class T>LinkedList<T>::LinkedList(const LinkedList<T>& L) //拷贝构造函数{front = rear = NULL;prevPtr = currPtr = NULL;size = 0;position = -1;copy(L);}template <class T>LinkedList<T>::~LinkedList() //析构函数{clear();}template <class T>LinkedList<T>& LinkedList<T>::operator=(const LinkedList<T>& L)//重载"="{if (this == &L) // 不能将链表赋值给它自身return *this;clear();copy(L);return *this;}template <class T>int LinkedList<T>::getSize() const //返回链表大小的函数{return size;}template <class T>bool LinkedList<T>::isEmpty() const //判断链表为空否{return size == 0;}template <class T>void LinkedList<T>::reset(int pos) //将链表当前位置设置为pos{int startPos;if (front == NULL) // 如果链表为空,返回return;if (pos < 0 || pos > size - 1) // 如果指定位置不合法,中止程序{std::cerr << "Reset: Invalid list position: " << pos << endl;return;}// 设置与遍历链表有关的成员if (pos == 0) // 如果pos为0,将指针重新设置到表头{prevPtr = NULL;currPtr = front;position = 0;}else // 重新设置 currPtr, prevPtr, 和 position{currPtr = front->nextNode();prevPtr = front;startPos = 1;for (position = startPos; position != pos; position++){prevPtr = currPtr;currPtr = currPtr->nextNode();}}}template <class T>void LinkedList<T>::next() //将prevPtr和currPtr向前移动一个结点{if (currPtr != NULL){prevPtr = currPtr;currPtr = currPtr->nextNode();position++;}}template <class T>bool LinkedList<T>::endOfList() const // 判断是否已达表尾{return currPtr == NULL;}template <class T>int LinkedList<T>::currentPosition() const // 返回当前结点的位置{return position;}template <class T>void LinkedList<T>::insertFront(const T& item) // 将item插入在表头{if (front != NULL) // 如果链表不空则调用Resetreset();insertAt(item); // 在表头插入}template <class T>void LinkedList<T>::insertRear(const T& item) // 在表尾插入结点{Node<T> *nNode;prevPtr = rear;nNode = newNode(item); // 创建新结点if (rear == NULL) // 如果表空则插入在表头front = rear = nNode;else{rear->insertAfter(nNode);rear = nNode;}currPtr = rear;position = size;size++;}template <class T>void LinkedList<T>::insertAt(const T& item) // 将item插入在链表当前位置{Node<T> *nNode;if (prevPtr == NULL) // 插入在链表头,包括将结点插入到空表中{nNode = newNode(item, front);front = nNode;}else // 插入到链表之中. 将结点置于prevPtr之后{nNode = newNode(item);prevPtr->insertAfter(nNode);}if (prevPtr == rear) //正在向空表中插入,或者是插入到非空表的表尾{rear = nNode; //更新rearposition = size; //更新position}currPtr = nNode; //更新currPtrsize++; //使size增值}template <class T>void LinkedList<T>::insertAfter(const T& item) // 将item 插入到链表当前位置之后{Node<T> *p;p = newNode(item);if (front == NULL) // 向空表中插入{front = currPtr = rear = p;position = 0;}else // 插入到最后一个结点之后{if (currPtr == NULL)currPtr = prevPtr;currPtr->insertAfter(p);if (currPtr == rear){rear = p;position = size;}elseposition++;prevPtr = currPtr;currPtr = p;}size++; // 使链表长度增值}template <class T>T LinkedList<T>::deleteFront() // 删除表头结点{T item;reset();if (front == NULL){cerr << "Invalid deletion!" << endl;exit(1);}item = currPtr->data;deleteCurrent();return item;}template <class T>void LinkedList<T>::deleteCurrent() // 删除链表当前位置的结点{Node<T> *p;if (currPtr == NULL) // 如果表空或达到表尾则出错{cerr << "Invalid deletion!" << endl;exit(1);}if (prevPtr == NULL) // 删除将发生在表头或链表之中{p = front; // 保存头结点地址front = front->nextNode(); //将其从链表中分离}else //分离prevPtr之后的一个内部结点,保存其地址p = prevPtr->deleteAfter();if (p == rear) // 如果表尾结点被删除{rear = prevPtr; //新的表尾是prevPtrposition--; //position自减}currPtr = p->nextNode(); // 使currPtr越过被删除的结点freeNode(p); // 释放结点,并size--; //使链表长度自减}template <class T>T& LinkedList<T>::data() //返回一个当前结点数值的引用{if (size == 0 || currPtr == NULL) // 如果链表为空或已经完成遍历则出错{cerr << "Data: invalid reference!" << endl;exit(1);}return currPtr->data;}template <class T>void LinkedList<T>::clear() //清空链表{Node<T> *currPosition, *nextPosition;currPosition = front;while (currPosition != NULL){nextPosition = currPosition->nextNode(); //取得下一结点的地址freeNode(currPosition); //删除当前结点currPosition = nextPosition; //当前指针移动到下一结点}front = rear = NULL;prevPtr = currPtr = NULL;size = 0;position = -1;}#endif //LINKEDLIST_H
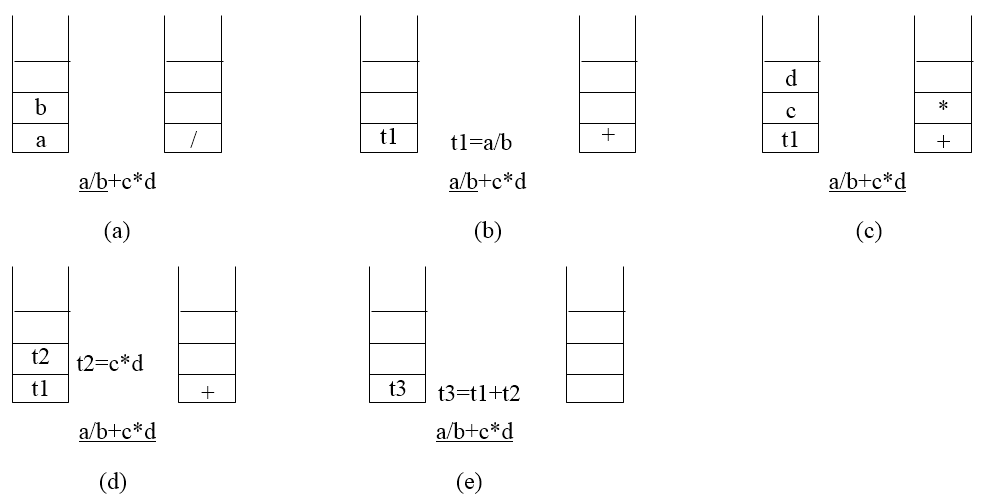
五、栈
栈是只能从一端访问的线性群体,可以访问的这一端称栈顶,另一端称栈底。栈是一种后进先出的数据结构。
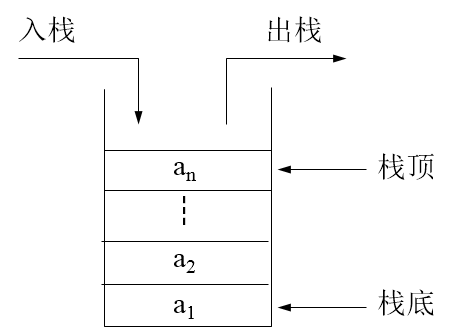
栈的应用举例:
栈的基本状态
- 栈空
- 栈满
- 一般状态
栈的基本操作
- 初始化
- 入栈
- 出栈
- 清空栈
- 访问栈顶元素
- 检测栈的状态(满、空)
类模板代码
//Stack.h#ifndef STACK_H#define STACK_H#include <cassert>template <class T, int SIZE = 50>class Stack {private:T list[SIZE];int top;public:Stack();void push(const T &item);T pop();void clear();const T &peek() const;bool isEmpty() const;bool isFull() const;};//模板的实现template <class T, int SIZE>Stack<T, SIZE>::Stack() : top(-1) { }template <class T, int SIZE>void Stack<T, SIZE>::push(const T &item) {assert(!isFull());list[++top] = item;}template <class T, int SIZE>T Stack<T, SIZE>::pop() {assert(!isEmpty());return list[top--];}template <class T, int SIZE>const T &Stack<T, SIZE>::peek() const {assert(!isEmpty());return list[top]; //返回栈顶元素}template <class T, int SIZE>bool Stack<T, SIZE>::isEmpty() const {return top == -1;}template <class T, int SIZE>bool Stack<T, SIZE>::isFull() const {return top == SIZE - 1;}template <class T, int SIZE>void Stack<T, SIZE>::clear() {top = -1;}#endif //STACK_H
六、队列
队列类模板
队列是只能向一端添加元素,从另一端删除元素的线性群体

队列的基本状态
- 队空
- 队满
- 一般状态
队空
- 队列中没有元素(以数组容纳的队列为例)

队满
- 队列中元素个数达到上限(以数组容纳的队列为例)
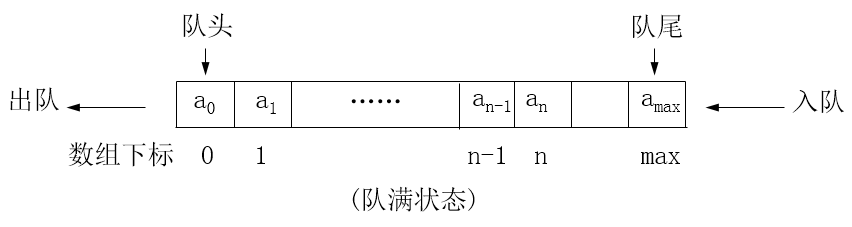
一般状态
- 队列中有元素,但未达到队满状态(以数组容纳的队列为例)
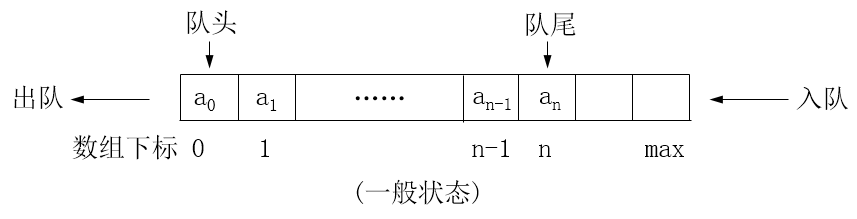
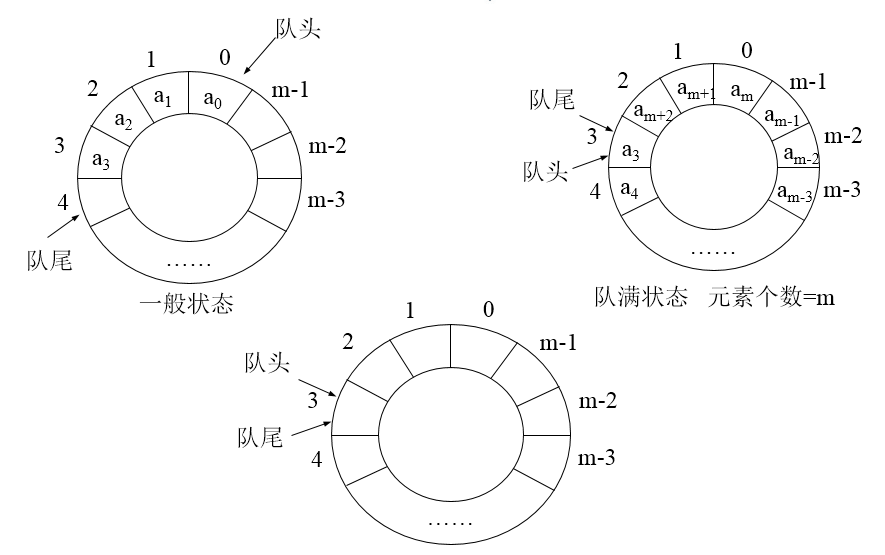
循环队列
- 在想象中将数组弯曲成环形,元素出队时,后继元素不移动,每当队尾达到数组最后一个元素时,便再回到数组开头。
例9-10 队列类模板
//Queue.h
#ifndef QUEUE_H
#define QUEUE_H
#include <cassert>
//类模板的定义
template <class T, int SIZE = 50>
class Queue {
private:
int front, rear, count; //队头指针、队尾指针、元素个数
T list[SIZE]; //队列元素数组
public:
Queue(); //构造函数,初始化队头指针、队尾指针、元素个数
void insert(const T &item); //新元素入队
T remove(); //元素出队
void clear(); //清空队列
const T &getFront() const; //访问队首元素
//测试队列状态
int getLength() const;//求队列长度
bool isEmpty() const;//判断队列空否
bool isFull() const;//判断队列满否
};
//构造函数,初始化队头指针、队尾指针、元素个数
template <class T, int SIZE>
Queue<T, SIZE>::Queue() : front(0), rear(0), count(0) { }
template <class T, int SIZE>
void Queue<T, SIZE>::insert (const T& item) {//向队尾插入元素
assert(count != SIZE);
count++; //元素个数增1
list[rear] = item; //向队尾插入元素
rear = (rear + 1) % SIZE; //队尾指针增1,用取余运算实现循环队列
}
template <class T, int SIZE> T Queue<T, SIZE>::remove() {
assert(count != 0);
int temp = front; //记录下原先的队首指针
count--; //元素个数自减
front = (front + 1) % SIZE;//队首指针增1。取余以实现循环队列
return list[temp]; //返回首元素值
}
template <class T, int SIZE>
const T &Queue<T, SIZE>::getFront() const {
return list[front];
}
template <class T, int SIZE>
int Queue<T, SIZE>::getLength() const { //返回队列元素个数
return count;
}
template <class T, int SIZE>
bool Queue<T, SIZE>::isEmpty() const { //测试队空否
return count == 0;
}
template <class T, int SIZE>
bool Queue<T, SIZE>::isFull() const { //测试队满否
return count == SIZE;
}
template <class T, int SIZE>
void Queue<T, SIZE>::clear() { //清空队列
count = 0;
front = 0;
rear = 0;
}
#endif //QUEUE_H
七、排序
排序是将一个数据元素的任意序列,重新排列成一个按关键字有序的序列。
- 数据元素: 数据的基本单位。在计算机中通常作为一个整体进行考虑。一个数据元素可由若干数据项组成。
- 关键字: 数据元素中某个数据项的值,用它可以标识(识别)一个数据元素。
- 在排序过程中需要完成的两种基本操作
- 比较两个数的大小
- 调整元素在序列中的位置
内部排序与外部排序
- 内部排序:待排序的数据元素存放在计算机内存中进行的排序过程。
- 外部排序:待排序的数据元素数量很大,以致内存存中一次不能容纳全部数据,在排序过程中尚需对外存进行访问的排序过程。
几种简单的内部排序方法
最坏情况下的时间复杂度都是n*n
- 插入排序
- 选择排序
- 交换排序
插入排序
每一步将一个待排序元素按其关键字值的大小插入到已排序序列的适当位置上,直到待排序元素插入完为止。
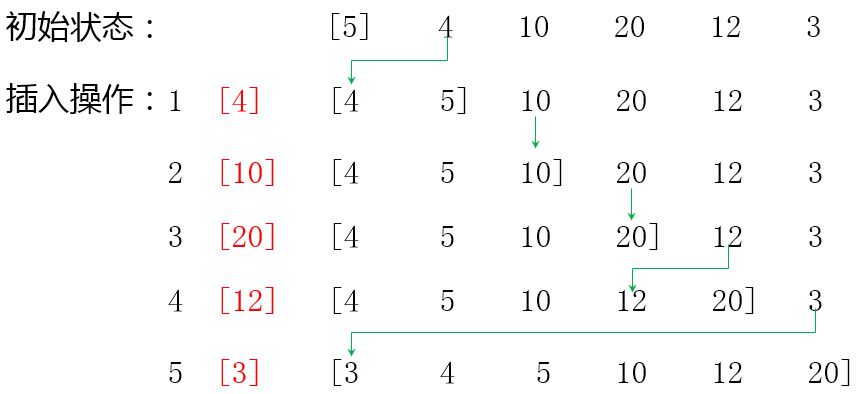
template <class T>
void insertionSort(T a[], int n) {
int i, j;
T temp;
for (int i = 1; i < n; i++) {
int j = i;
T temp = a[i];
while (j > 0 && temp < a[j - 1]) {
a[j] = a[j - 1];
j--;
}
a[j] = temp;
}
}
这个程序其实就是每个数先保存一下,然后比较是不是比前一个数小,是的话让前一个数往后挪一挪(挤占了内存数据)给这个数腾个空间,然后把保存的值放进去。
选择排序
每次从待排序序列中选择一个关键字最小的元素,(当需要按关键字升序排列时),顺序排在已排序序列的最后,直至全部排完。

template <class T>
void mySwap(T &x, T &y) {
T temp = x;
x = y;
y = temp;
}
template <class T>
void selectionSort(T a[], int n) {
for (int i = 0; i < n - 1; i++) {
int leastIndex = i;
for (int j = i + 1; j < n; j++)
if (a[j] < a[leastIndex])
leastIndex = j;
mySwap(a[i], a[leastIndex]);
}
}
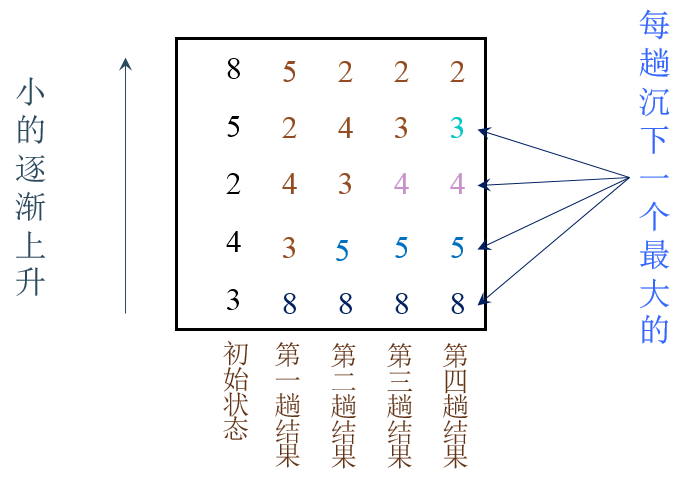
交换排序(起泡排序)
两两比较待排序序列中的元素,并交换不满足顺序要求的各对元素,直到全部满足顺序要求为止。
template <class T>
void mySwap(T &x, T &y) {
T temp = x;
x = y;
y = temp;
}
template <class T>
void bubbleSort(T a[], int n) {
int i = n – 1;
while (i > 0) {
int lastExchangeIndex = 0;
for (int j = 0; j < i; j++)
if (a[j + 1] < a[j]) {
mySwap(a[j], a[j + 1]);
lastExchangeIndex = j;
}
i = lastExchangeIndex;
}
}
八、查找
顺序查找
从序列的首元素开始,逐个元素与待查找的关键字进行比较,直到找到相等的。若整个序列中没有与待查找关键字相等的元素,就是查找不成功。
template <class T>
int seqSearch(const T list[], int n, const T &key) {
for(int i = 0; i < n; i++)
if (list[i] == key)
return i;
return -1;
}
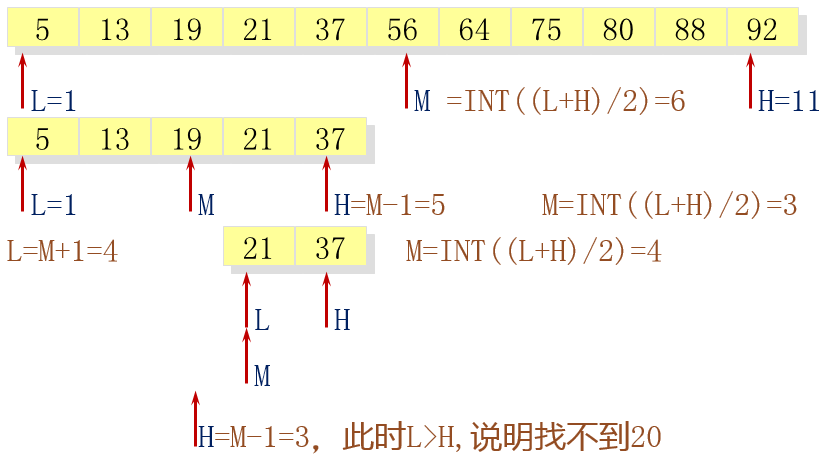
二分查找
对于已按关键字排序的序列,经过一次比较,可将序列分割成两部分,然后只在有可能包含待查元素的一部分中继续查找,并根据试探结果继续分割,逐步缩小查找范围,直至找到或找不到为止。
template <class T>
int binSearch(const T list[], int n, const T &key) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (key == list[mid])
return mid;
else if (key < list[mid])
high = mid – 1;
else
low = mid + 1;
}
return -1;
}