定义

树（tree）是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

常用语

  • 路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为“路
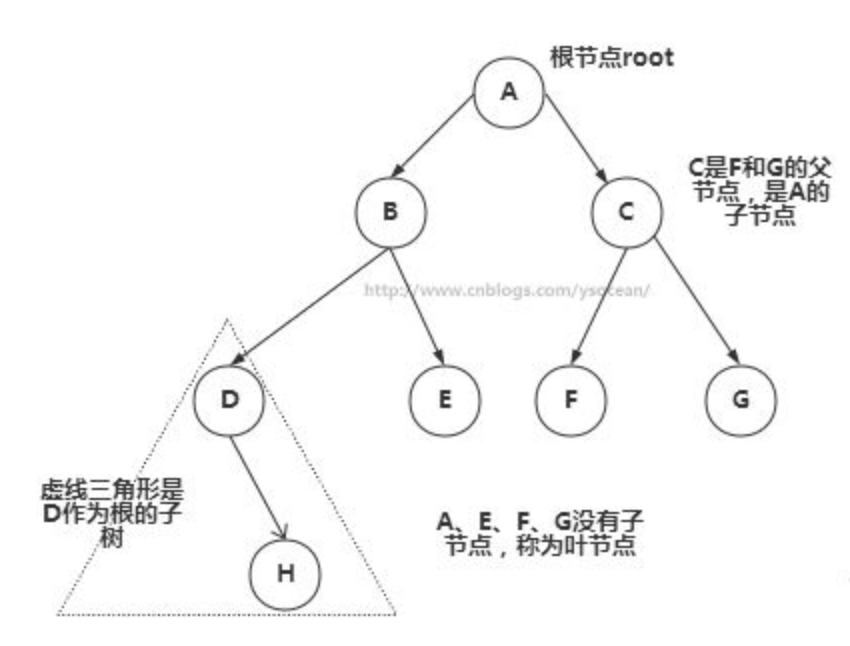
  • 根：树顶端的节点称为根。一棵树只有一个根，如果要把一个节点和边的集合称为树，那其他任何一个节点都必须有且只有一条路径。A是根节点。
  • 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；B是D的父节点。
  • 子节点：一个节点含有的子树的根节点称为该节点的子节点；D是B的子节点。
  • 兄弟节点：具有相同父节点的节点互称为兄弟节点；比如上图的D和E就互称为兄弟节
  • 叶节点：没有子节点的节点称为叶节点，也叫叶子节点，比如上图的H、E、F、G都是叶字节点
  • 子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中
  • 节点的层次：从根开始定义，根为第一层，根的子节点为第二层，以此类推。
  • 深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0
  • 高度：对于任意节点n，n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；

image.png

树的特点

  • 每个节点有零个或多个子节点
  • 没有父节点的节点称为根节点
  • 每一个非根节点有且仅有一个父节点
  • 除了根节点外，每个子节点可以分为多个不相交的子树

树的种类

  • 二叉树
    • 完全二叉树
      • 满二叉树
    • 平衡二叉树
    • 二叉搜索树
  • 霍夫曼树
  • B树

    二叉树

    定义

    树的每个节点最多只能有两个子节点。

二叉树的结构

  1. template <typename T>
  2. struct binaryTreeNode
  3. {
  4.     T element;
  5.     binaryTreeNode<T> *leftChild, *rightChild;
  6. };

二叉树基本方法

输出节点数值

template <typename T>
void printvalue(binaryTreeNode<T> *t)
{
    cout << t->element << "  ";
}

查找节点

插入新节点

void BST_insert( binaryTreeNode<T> *node,  binaryTreeNode<T> *insert_node) {
    if (insert_node->element < node->element) {
        if (node->leftChild) {
            BST_insert(node->leftChild, insert_node);
        } else {
            node->leftChild = insert_node;
        }
    } else {
        if (node->rightChild) {
            BST_insert(node->rightChild, insert_node);
        } else {
            node->rightChild = insert_node;
        }
    }
}

删除节点

高度

template <typename T>
int height(binaryTreeNode<T> *t)
{
    if(t == NULL)
        return 0;
    int hl = height(t->leftChild);
    int hr = height(t->rightChild);
    if (hl > hr)
        return ++hl;
    else
        return ++hr;
}

二叉树的遍历

前序遍历

template <typename T>
void preOrder(binaryTreeNode<T> *t) 
{
    if(t != NULL)
    {
        printvalue(t);                      // 输出元素
        preOrder(t->leftChild);     // 前序遍历左子树
        preOrder(t->rightChild);        // 前序遍历右子树
    }
}

中序遍历

template <typename T>
void preOrder(binaryTreeNode<T> *t) 
{
    if(t != NULL)
    {
        preOrder(t->leftChild);     // 前序遍历左子树
        printvalue(t);                      // 输出元素
        preOrder(t->rightChild);        // 前序遍历右子树
    }
}

后序遍历

template <typename T>
void postOrder(binaryTreeNode<T> *t)
{
    if(t != NULL)
    {
        postOrder(t->leftChild);        // 后序遍历左子树
        postOrder(t->rightChild);     // 后序序遍历右子树
        printvalue(t);                         // 输出元素
    }
}

层序遍历

vector<T> levelOrder(binaryTreeNode<T> *t)
{
    if (t == NULL)
        return;
    queue<binaryTreeNode<T> *> q;
    vector<T> res;
    q.push(t);
    while (!q.empty())
    {
        binaryTreeNode<T> *tt;
        tt = q.front();
        res.push_back(tt->element);
        q.pop();
        if (t->leftChild != NULL)
            q.push(t->leftChild);
        if (t->rightChild != NULL)
            q.push(t->rightChild);
    }
    return res;
}